You may have heard a math teacher or two say that math is a language. If that is true, then algebraic rules and notation should be considered the grammar and punctuation of the language of math!
Some students who struggle with math are confused by how to apply the rules and interpret the notation. In this video, we will focus on the notation and interpretation of exponents. This video will also focus on the meaning of exponents that are natural numbers, also referred to as “counting numbers” (i.e., 1, 2, 3, etc.). Other types of exponents are interpreted differently and will be covered in other videos.
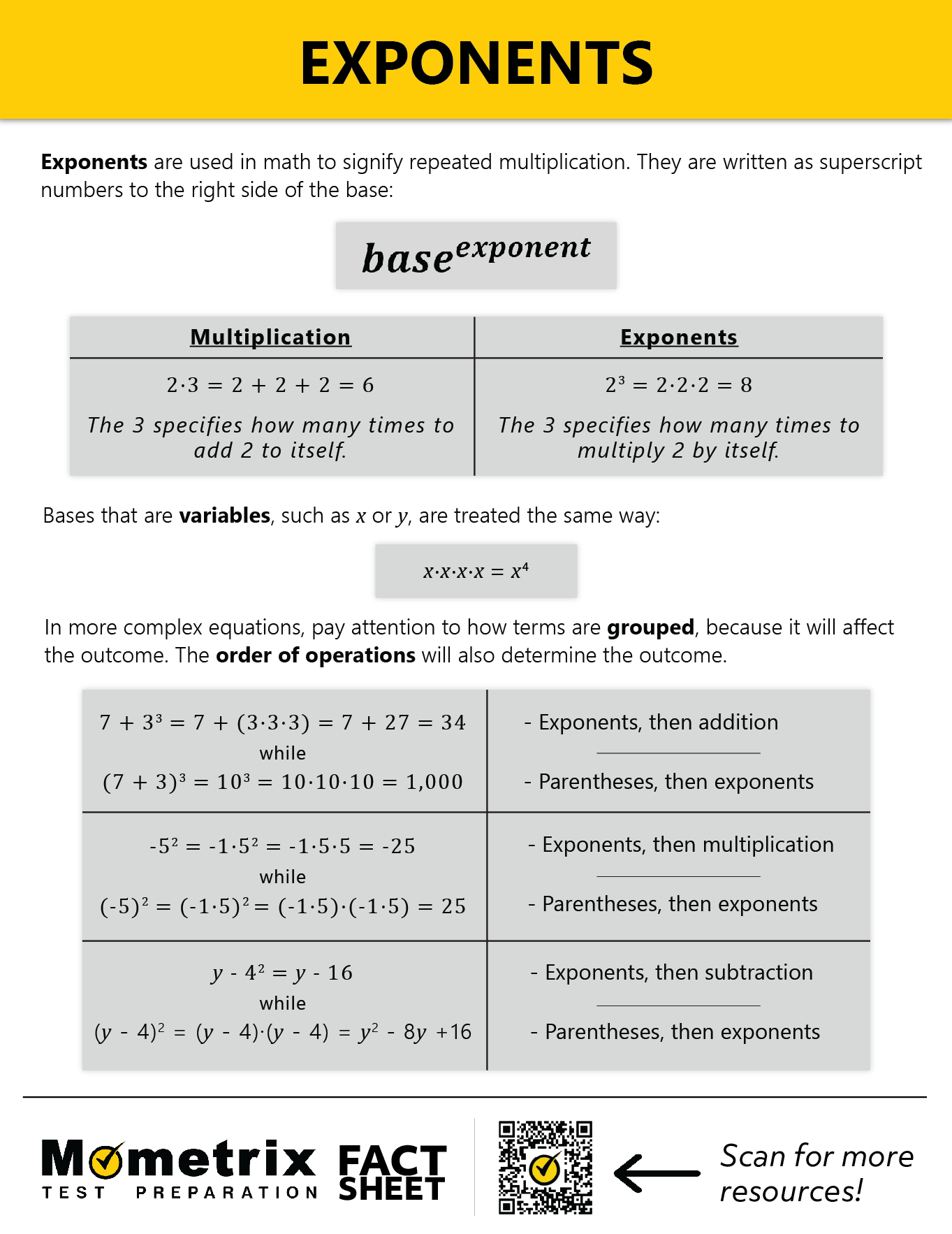
Terminology
Let’s start by quickly reviewing some terminology. An exponent is written as a superscript on a number or algebraic expression, which is referred to as the base. There are a few ways to verbalize a “power.” \(5^2\) can be read as “five squared,” “five to the second,” “five raised to the second power,” or “five raised to the power of 2.” In any case, the exponent should be interpreted as repeated multiplication.
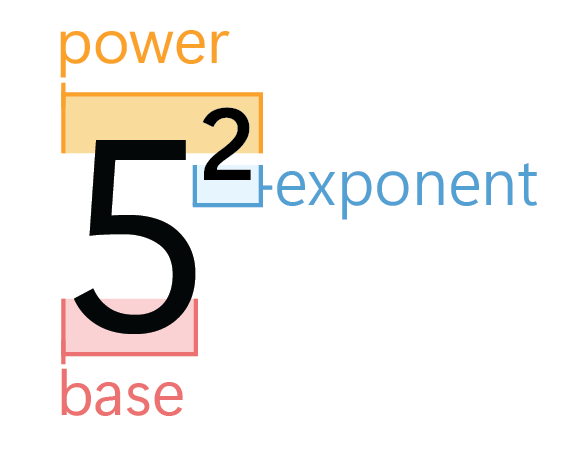
Whatever is defined as the base should be multiplied by itself however many times the exponent implies. For example, \(5^2=5 \times 5\). This can then easily be evaluated as 25.
Example 1
Let’s look at some examples. For \(7^3\), the base is 7 and the exponent is 3. This can be read as “7 to the third” or “seven cubed.” Raising a base of 7 to the power of 3 means to multiply 7 by itself 3 times: \(7^3=7 \times 7 \times 7\). Seven times itself three times equals 343.
Example 2
Let’s try another one, but this one will look a little different: \((-2)^2\). It is important to point out that parentheses are being used with this example to define the base. Negative 2 is being raised to the second power. The interpretation is the same! Simply multiply negative 2 by itself twice. Multiplying two negative numbers using parentheses results in a positive value: \((-2)(-2) = 4\).
Example 3
But, if we were to take the parentheses away and instead say \(-2^2\), then our answer would be negative 4. Why? Because the 2 is squared before the effects of the negative take place. Since \(2^2\) is four, \(-2^2\) is -4.
Example 4
Let’s try another one with negatives: \((-5)^3\) \((-5)^3=(-5)(-5)(-5)= -125\). Powers of ten are used frequently in math and science applications. Scientific notation uses powers of ten to express very large or small values in an efficient, organized manner, but we’ll dive into that topic in another video.
Example 5
Exponents are also used to raise algebraic expressions to powers, but the meaning is the same: multiply whatever the base is by itself however many times that is indicated by the exponent! Here is an example: \(x^3=x \times x \times x\). As you can see, the notation \(x^3\) is a more efficient way to write the expanded version of \(x \times x \times x\).
Example 6
Here’s another example: \(2x^3=2 \times x \times x \times x\). Notice that the base is \(x\) here. Adding parentheses in an expression changes the meaning: \((2x)^3=(2x)(2x)(2x)\) The parentheses define the base as “2x.” Rearranging the expanded expression shows how the power is simplified: \((2x)^3=2 \times 2 \times 2 \times x \times x \times x=8x^3\)
Example 7
Let’s try one more example before we go: \((x+2)^2\). Once again, parentheses are used to define the base to be \(x+2\). The exponent of 2 instructs you to multiply this base by itself twice. Here are two binomial expressions: \((x+2)^2=(x+2)(x+2) \). Multiplying these two binomial expressions results the quadratic expression \((x+2)^2=(x+2)(x+2)\)\(=x^2+4x+4\).
So, as long as you can identify the base, the multiplication of that base by itself becomes pretty straightforward. As mentioned, the interpretation of notation in math is half the battle! Practicing the basics is key in order to gain confidence for more complicated math content.
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What are exponents in math?
A
Exponents are used in math to abbreviate an otherwise very long number. For example, if you were making calculations with the value 184,528,125 it would be much more efficient to express this value as \(45^5\). Exponents are used as a more efficient way to represent repeated multiplication. For example, instead of writing \(3\times3\times3\times3\times3\times3\) we can simply write \(3^6\).
Q
How do you figure out exponents?
A
When an exponent is used, it represents repeated multiplication. The “base” represents the number being multiplied by itself, and the “exponent” represents how many times it is multiplied. Calculating a value such as \(4^9\) means 4 will be multiplied by itself 9 times. In other words, \(4\times4\times4\times4\times4\times4\times4\times4\times4\), which equals 262,144.
Q
What are the 5 rules of exponents?
A
There are five main rules to remember when working with exponents:
Rule 1: The product rule states that when you multiply exponents that have the same base, you simply add the exponents. For example, \(2^3\times2^4=2^{3+4}=2^7\).
Rule 2: The quotient rule states that when you divide exponents that have the same base, you simply subtract the exponents. For example, \(\frac{2^5}{2^3}=2^{5-3}=2^2\).
Rule 3:The power rule states that when you raise a power to a power, you can multiply the powers together. For example, \(2^{3^4}=2^{3\times4}=2^{12}\).
Rule 4:The zero rule states that any number raised to a power of zero, is always equal to one. For example, \(4^0=1\).
Rule 5: The one rule of exponents states that any number raised to the power of one is always equal to itself. For example, \(8^1=8\).
Q
What are the 4 types of exponents?
A
The 4 types of exponents are: positive, negative, zero, and rational. Positive exponents tell you how many times to multiply a base by itself. This will generally result in a very large number. Negative exponents tell you how many times to divide a base by itself. This will generally result in a very small number. An exponent of zero will always be equal to one. A rational exponent means there is a fraction as the exponent.
Q
Why do we use exponents?
A
Exponents are used as a shorthand way to write extremely large or extremely small numbers. For example, \(6^8\) is more efficient than writing 1,679,616. Similarly, \(6^{-3}\) is more efficient than writing 0.0046296296. Exponents are also used as a shorthand way to express repeated multiplication. Instead of writing \(7\times7\times7\times7\times7\times7\) we can simply write \(7^6\).
Q
What is the difference between a power and an exponent?
A
The terms “power” and “exponent” essentially mean the same thing. For example, “five to the third power” represents a base of five and an exponent of three. Often these two terms are used interchangeably.
Q
Are indices and exponents the same?
A
An index, or an indice, is another name for an exponent. The index of a number tells you how many times to multiply the base by itself. For example, the index of \(4^2\) is 2. The exponent of \(4^2\) is also 2. The terms index and exponent are interchangeable.
Q
What do positive exponents represent?
A
A positive exponent tells you how many times to multiply the base by itself. For example, if the base is 8 and the exponent is 4, 8 would be multiplied by itself 4 times: \(8^4=8\times8\times8\times8=4{,}096\).
Q
What is the use of exponents in our daily life?
A
Exponents are often used in our daily life as a way to write extremely large or extremely small numbers efficiently. Exponents represent repeated multiplication in a compact format.
For example, exponents are used to measure the strength of earthquakes. A level 1 earthquake has a magnitude of \(1\times10^1\), a level 2 earthquake has a magnitude of \(1\times10^2\), and so on. Exponents allow us to make sense of very small and very large numbers in a way that is concise and easy to read.
Q
How are exponents used in science?
A
Exponents are often used in science when describing very small or very large numbers. In many cases, scientific notation is used to write these small or large values. Scientific notation requires a base to be multiplied by a power of ten. For example, \(2.4\times10^7\). The power, or exponent, can be positive or negative. Positive exponents will result in large numbers, and negative exponents will result in small numbers.
Q
How are exponents used in engineering?
A
Engineers use exponents because they are frequently working with very large or very small measurements. For example, a civil engineer might be working with calculations regarding the weight of a massive bridge. These measurements could be in the tens of thousands, so it is often most efficient to express them using positive exponents. On the other end of the spectrum, chemical engineers often work with values that are extremely small. These values are most efficiently written using negative exponents.
Q
How are negative exponents used in real life?
A
Negative exponents tell you how many times to divide a base by itself. For example, \(8^{-4}\) represents \(1÷8÷8÷8÷8\). \(5^{-6}\) represents \(1÷5÷5÷5÷5÷5÷5\). Negative exponents are used in many real-world situations involving extremely small numbers. For example, physicists make calculations using values as small as \(10^{-19}\) meters when measuring subatomic particles such as quarks.
What is an Exponent? (PDF)
Exponent Practice Problems
\(2^4\)
The correct answer is 16.
\(2^4=2\times2\times2\times2=16\)
\((3x)^3\)
The correct answer is \(27x^3\).
\((3x)^3=(3x)(3x)(3x)=27x^3\)
\((x+4)^2\)
The correct answer is \(x^2+8x+16\).
\((x+4)^2=(x+4)(x+4)\)
To multiply polynomials, multiply each part of the first polynomial by each part of the second polynomial.
\((x+4)(x+4)\)\(=x^2+4x+4x+16\)\(=x^2+8x+16\)
\((-7)^3\)
The correct answer is -343.
\((-7)^3=(-7)(-7)(-7)=-343\)
Since there are three negatives, the final answer is negative.
\((x-7)^2\)
The correct answer is \(x^2-14x+49\).
\((x-7)^2=(x-7)(x-7)\)
To multiply polynomials, multiply each part of the first polynomial by each part of the second polynomial.
\((x-7)(x-7)\)\(=x^2-7x-7x+49\)\(=x^2-14x+49\)