Hi, and welcome to this video on the laws of exponents!
Working with polynomial, radical, and rational functions often times requires us to perform algebraic operations with powers. Recall that a power is nothing more than a base that is raised to an exponent.
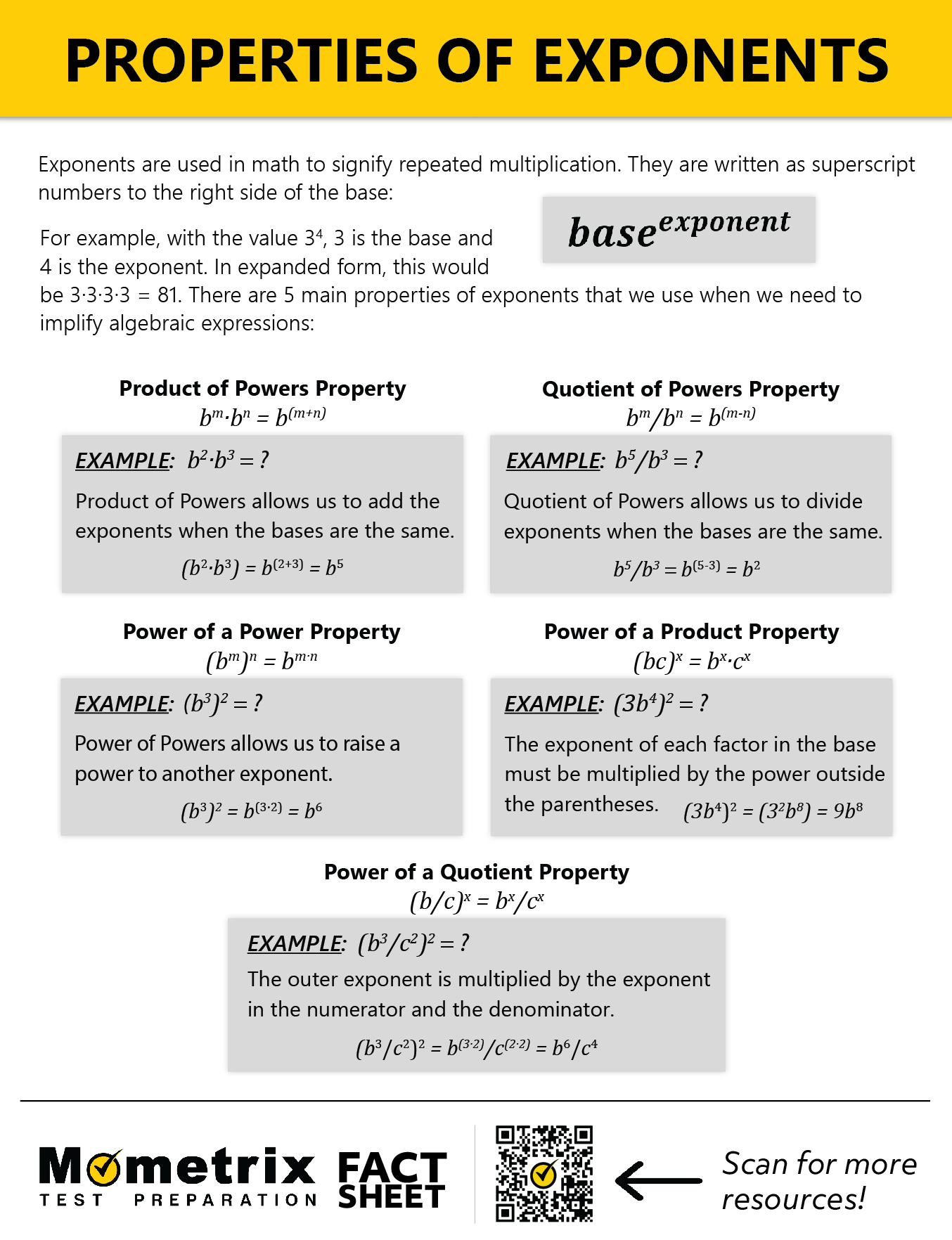
Let’s take a look at the properties of exponents that are used to simplify algebraic expressions with powers.
Product of Powers
The product of powers property applies to powers with the same base. When asked to multiply powers with the same base, simply add the exponents. For example:
This rule makes intuitive sense if you expand each power like this:
Counting up the bases of \(b\) that are being multiplied results in 5.
Therefore, the general form of the product of powers rule is:
Quotient of Powers
The quotient of powers property also applies to powers with the same base; however, the rule requires the subtraction of exponents. Let’s look at an example:
Canceling out common factors of \(b\) from the numerator and the denominator would simplify to be \(b^2\).
The quotient of powers property allows a quicker, more efficient result. Simply subtract the exponent of the denominator from the exponent of the numerator: \(5-3=2\).
The general form for quotient of powers property is:
Power of a Power
The power of a power property allows us to raise a power to another exponent. Once again, expanding an expression makes understanding the rule a bit easier. Suppose the power \(b^3\) is squared:
In expanded form it would look like this: \((b\cdot b\cdot b)(b\cdot b\cdot b)\). Using the product of powers property, or simply counting up the bases of \(b\), results in \(b^6\).
The general form of this property is:
Power of a Product
Expanding on the power of a power property results in additional tools that are used to simplify expressions with powers.
For example, suppose the base of a power is a monomial with a coefficient and a variable.
\((3b^4)^2\) expands to \((3b^4)(3b^4)\). Rearranging the factors to group the coefficients and the powers with the same base, \(b\), and simplifying gives us \((3 \cdot 3 \cdot b^4 \cdot b^4)=9b^8\).
This is called the power of a product property and illustrates that the exponent of each factor in the base must be multiplied by the power outside the parentheses.
The general form for the power of product property is:
Power of Quotient
The power of quotient property is similar in that the exponent of a rational base is multiplied by the exponents in both the numerator and denominator. Let’s look at some examples:
The product of powers property results in the simplified expression \(\frac{b^{6}}{c^{4}}\).
However, applying the power of quotient property directly is often more efficient:
Here’s another example:
Rearranging factors and applying the product of powers property results in:
If we were to apply the power of quotient property, it would look like this:
The general rule for the power of quotient property is:
As you can see, these rules are essential in simplifying expressions within our work with various algebraic functions.
Thanks for watching this review covering the laws of exponents! Happy studying!
Frequently Asked Questions
Q
What is the formula for product of powers?
A
The product of powers rule says that when multiplying exponents with the same base, you can find the product by keeping the base and adding the exponents. For example, to find the product of \(x^4·x^3\), we would keep the base \(x\), and add the exponents, therefore \(x^4·x^3=x^4+3=x^7\). The rule works because when we expand each term, we get \((x·x·x·x)·(x·x·x)\), which is equivalent to \(x^7\). The general formula that is used to represent this rule is \(a^m·a^n=a^{m+n}\).
Q
What is the product of powers property?
A
The product of powers property or rule states that when multiplying exponents with the same base, you find the product by keeping the base and adding the exponents. The formula for the rule is \(a^m·a^n=a^{m+n}\). For example, the \(w^5\times w^7=w^{5+7}=w^{12}\).
Q
What is an example of quotient of powers?
A
The quotient of powers rule states that when dividing exponents with the same base, we keep the base and subtract the exponents. The general formula for the rule is \(a^m\div a^n=a^{m-n}\). An example of the quotient of powers is \(x^8\div x^3=x^{8-3}=x^5\).
Q
What is the quotient rule for exponents?
A
The quotient rule for exponents says, when dividing exponents with the same base, we keep the base and subtract the exponents. The general form of the rule is \(a^m\div a^n=a^{m-n}\). For example, to find the quotient of \(y^{11}\div y^4\), we keep the base and subtract the exponents to get \(y^7\).
Q
Can you have a power of a power?
A
Yes, you can have a power of a power. The power of a power rule says, when a number with an exponent is raised to another exponent, we can simplify the exponent by keeping the base and multiplying the exponents. The general form of the rule is \((a^m)^n=a^{m·n}\). For example, to find the power of the power of the expression, \((x^2)^7=x^{2·7}=x^{14}\).
Q
What is the power of power rule in math?
A
The power of power rule states that when a number with an exponent is raised to another exponent, the expression can be simplified by keeping the base and multiplying the exponents. The general form of the rule is \((a^m)^n=a^{m·n}\). We can see why the rule works by expanding the exponents. For example, we will expand the expression \((y^3)^2\). Inside the parentheses, we expand \(y^3\), \((y·y·y)^2\). Now we raise the expression inside the parentheses to the second power: \(y·y·y·y·y·y\), which as you can see is \(y^6\). If we apply the rule, we get the following, \((y^3)^2=y^{3·2}=y^6\).
Q
What is the power of product property?
A
The power of product property or rule states that if two numbers multiplied by one another are raised to a certain power, then each number is raised to that power and then the numbers are multiplied. The general form of the rule is \((ab)^m=a^mb^m\). For example, to simplify the expression \((3x)^3\), we raise each term inside the parentheses to the third power and then simplify: \((3x)^3=3^3x^3=27x^3\).
Q
What is the power of quotient property?
A
The power of quotient property states that if two numbers divided by one another are raised to a certain power, then each number is raised to that power and then the numbers are divided. The general form of the rule is \((\frac{a}{b})^m=\frac{a^m}{b^m}\). For example, to simplify the expression \((\frac{2}{4})^3\), we raise each number to the third power and then divide: \((\frac{2}{4})^3=\frac{2^3}{4^3}=\frac{8}{64}=\frac{1}{8}\).
Laws of Exponents PDF
Laws of Exponents Practice Questions
\(x^2×x^5=\)
The correct answer is \(x^7\). According to the product of powers property, when two numbers with the same base are multiplied together, the base will stay the same and the exponents are added.
\(x^2×x^5=x^{(2+5)}=x^7\)
\(y^6÷y^3=\)
The correct answer is \(y^3\). According to the quotient of powers property, when two numbers with the same base are divided, the base will stay the same and the exponents will be subtracted.
\(y^6÷y^3=y^{(6-3)}=y^3\)
\((z^2 )^8=\)
The correct answer is \(z^{16}\). According to the power of a power property, when a number with an exponent is raised to a power, the base stays the same and the exponents are multiplied.
\((z^2 )^8=z^{(2×8)}=z^{16}\)
Which of the following is a correct statement?
The correct answer is \((7×9)^3=7^3×9^3\). This is an example of the power of product property, which says: \((b×c)^x=b^x×c^x\). In other words, when two numbers are multiplied together and then raised to a power, it is the same as saying the first number raised to the power times the second number raised to the power.
Which of the following statements is not true?
The correct answer is \((\frac{x^3}{y^2})^4=\frac{x^7}{y^6}\). According to the power of a power property, the correct statement should be \((\frac{x^3}{y^2})^4=\frac{x^{12}}{y^8}\). \((x×y)^3=x^3 y^3\) is an example of the power of a product property. \((x^5)^4=x^{20}\) is an example of the power of a power property. And \(y^7×y^9=y^{16}\) is an example of the product of powers property.