Substitution and Elimination for Solving Linear Systems
Hi, and welcome to this video on using substitution and elimination to solve linear systems!
“Solving” a system of equations means to determine the exact \((x,y)\) coordinate that satisfies both of the equations in the system. The process of solving a system depends on the structure of the equations. Some systems can easily be solved by graphing both equations and determining the exact point of intersection, while other systems are more suitable to be solved
This video will focus on two of the algebraic approaches, namely substitution and elimination.
To solve a system of two equations with two variables, we are trying to find the exact point that satisfies both equations. What do I mean by “satisfy”?
That means that if you substitute that point into BOTH equations, you will have a “true” statement.
We also already mentioned that the “structure” of the system will determine which of the solving methods to use.
Substitution Method
The substitution method is typically used when one of the equations in the system is already solved for one of the variables. When this is the case, you can substitute the expression that the variable is equal to into the other equation:
For example:
\(y=x+2\)
and
\(x+2y= -5\)
Because we know that the variable \(y=x+2\), we can substitute \((x+2)\) for the variable \(y\) in the second equation:
\(x+2(x+2)=-5\)
Note that after the substitution, the \(y\)-variable is no longer in the equation.
At this point, we solve for \(x\) by distributing the coefficient of 2 into the parentheses.
\(x+2x+4= -5\)
Combine like terms, \(x+2x\), and gather the constants by subtracting 4 from both sides of the equation:
\(x+2x+4= -5\)
\(3x+4-4= -5-4\)
\(3x= -9\)
Then we’re going to divide both sides by 3 and this results in \(x=-3\).
At this point, we are halfway to our solution. In order to determine the \(y\)-variable, simply substitute \(x= -3\) into either of the original equations. Substituting into the first equation gives the quickest solution:
\(y=(-3)+2= -1\)
The solution for this system is the ordered pair \((-3,-1)\).
Let’s practice the substitution method by looking at one more problem together:
\(y=-2x+4\)
\(3x+2y=1\)
Because \(y\) is solved in terms of \(x\) in the first equation, substitute the expression \((-2x+4)\) for \(y\) in the second equation.
\(3x+2(-2x+4)=1\)
Distribute the 2 into the parentheses. Combine like terms and solve for \(x\):
\(3x-4x+8=1\)
\(-x+8=1\)
\(-x+8-8=1-8\)
\(-x=-7\)
\(x=7\)
Solve for \(y\) by substituting \(x= 7\) into the first equation of the system:
\(y=-2(7)+4\)
\(y= -14+4\)
\(y= -10\)
The ordered pair, \((7,-10)\), is the solution to this system.
To check your work, simply substitute this ordered pair into both equations to verify that you get a true statement.
Remember, these types of systems were well suited for the substitution method because one of the variables was already solved.
Elimination Method
For systems of equations that have two equations in “standard form,” the elimination method may be preferred. Recall that standard-form equations have both variable terms on one side of the equation and constant terms on the other.
The overall concept of this method is to “eliminate” one of the variables from the system by adding like terms of each equation together. A straightforward example of the elimination method is shown:
\(2x+y=1\)
\(x -y=8\)
Both of these equations are in standard form. If the equations are added by combining like terms, the \(y\)-variable is eliminated because the leading coefficients of the \(y\)-variables are of opposite signs:
\(3x+0y=9\)
\(3x=9\)
Solve for \(x\) by dividing both sides by 3, which results in \(x=3\). Now, as before, use this value to determine the value of \(y\) by substituting \(x=3\) into either of the original equations. Let’s use the second equation of the system because it is fairly simple:
\(3-y=8\)
To solve for \(y\), subtract 3 from both sides and divide by -1 for a solution of \(y=-5\). So the final solution to this system is the ordered pair \((3,-5)\).
As mentioned, that example was fairly straightforward because the coefficients of the \(y\)-variables canceled out when added. When coefficients do not cancel, you can use the Multiplication Property of Equality to multiply the equation by whatever value you need to eliminate.
Review
To wrap up, let’s see if you remember which method of solving would be most appropriate for the following systems:
1.
\(-3x − 3y = 3\)
\(y = −5x − 17\)
2.
\(−4x + y = 6\)
\(−5x − y = 21\)
Thanks for watching, and happy studying!
Linear System Practice Questions
Solve the system of equations using substitution.
\(x-2y=8\)
\(x+y=5\)
The correct answer is B: \((6, -1)\).
Let’s start by solving the second equation for x.
\(x+y=5\) becomes \(x=5-y\)
Now that we have isolated the variable x, let’s substitute this in for the x in the other equation.
\(x-2y=8\) becomes \((5-y)-2y=8\)
From here we can solve for y.
\(y=-1\)
Now let’s take this value for y, and plug it in to one of our original equations. Let’s use the second original equation.
\(x+y=5\) becomes \(x+(-1)=5\) and when we solve for x, we have \(x=6\)
The solution is the ordered pair \((6, -1)\).
Solve the system of equations using elimination.
\(12x-9y=37\)
\(8x+9y=23\)
The correct answer is A: \((3, -\frac{1}{9})\).
Elimination is a great choice for this problem because we can see that -9y and 9y will cancel out nicely. Let’s start by adding the two equations:
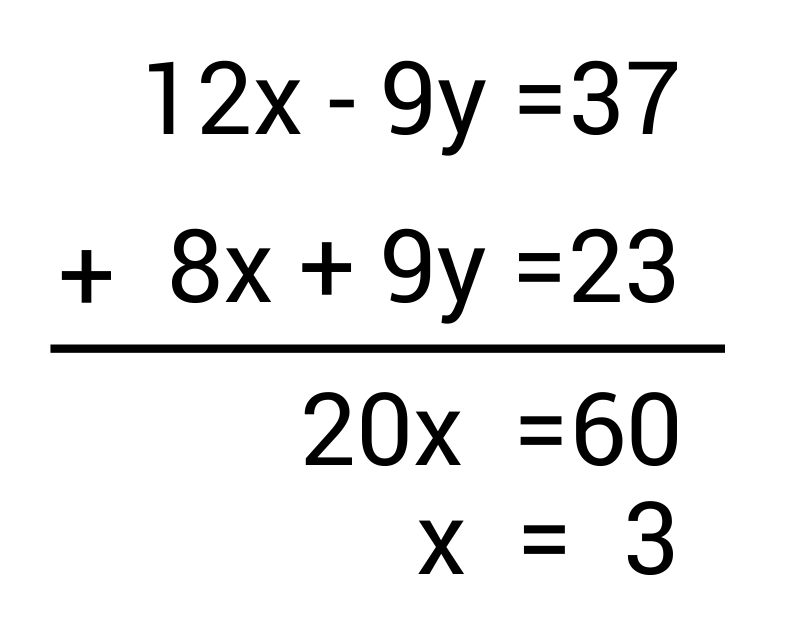
Now that we know \(x=3\), we can plug this in to one of our original equations in order to solve for y. Let’s use the second equation.
\(8x+9y=23\) becomes \(8(3)+9y=23\) and when we isolate the variable, we see that \(y=-\frac{1}{9}\)
Our solution is the ordered pair \((3, -\frac{1}{9})\).
Solve the system of equations using substitution.
\(3x-y=7\)
\(y-2=2x\)
The correct answer is D: \((9, 20)\).
Let’s start by solving the second equation for y:
\(y-2=2x\) becomes \(y=2x+2\)
Now that we have solved for y, we can substitute this into the other equation.
\(3x-y=7\) becomes \(3x-(2x+2)=7\) and when we solve for x, we have \(x=9\)
From here we can plug 9 in for x in one of the original equations in order to solve for y. Let’s use the second equation.
\(y-2=2x\) becomes \(y-2=2(9)\) and when simplified, \(y=20\)
Our solution is the ordered pair \((9, 20)\).
Farmer Frank operates a farm with chickens and pigs. The total number of animals on the farm is 100. The total number of animal legs is 270. How many pigs are on the farm? How many chickens are on the farm?
The correct answer is B: 35 pigs and 65 chickens.
We can solve this problem by setting up a system of equations. Let’s write two equations that are true for the scenario. One equation is based on the number of animals and the other equation is based on the number of legs, where c represents chickens and p represents pigs.
\(c+p=100\)
\(2c+4p=270\)
From here we can solve the first equation for p.
\(c+p=100\) becomes \(p=100-c\)
Now we plug this in for p in the other equation.
\(2c+4p=270\) becomes \(2c+4(100-c)=270\)
Now solve for c:
\(2c+4(100-c)=270\) becomes \(c=65\)
From here we can plug in the value of c into one of our original equations in order to solve for p.
\(c+p=100\) becomes \((65)+p=100\); therefore, \(p=35\)
Farmer Frank has 35 pigs and 65 chickens on his farm.
Mr. Parker wanted to treat his family so he took them all out to a movie. There are 15 people in his family including himself. The adult tickets were $10 and the children tickets were $5. The total ticket cost was $110. How many children and how many adults are in the family?
The correct answer is D: 8 children and 7 adults.
Let’s start by setting up two true equations that represent the scenario. One equation can represent the number of people and the other can represent cost, where a will represent adults and c will represent children.
\(a+c=15\)
\(10a+5c=110\)
Let’s solve the first equation for a.
\(a+c=15\) becomes \(a=15–c\)
Now let’s substitute this in for “a” in the other equation.
\(10a+5c=110\) now becomes \(10(15 -c)+5c=110\), which simplifies to \(c=8\)
Now that we know \(c=8\), we can plug this into one of the original equations in order to solve for a. Let’s use the first equation:
\(a+c=15\) becomes \(a+(8)=15\), so \(a=7\)
There are 8 children and 7 adults in the family.
