
Hi, and welcome to this video on the vertex of a parabola.
Introduction to Parabolas
The first curve most of us learn to graph is a parabola. Before that, we all learned to plot points on a number line and on a coordinate plane. Then we graphed the lines of linear equations, which only required two points and a ruler to keep things straight. Once we mastered that it was time for the parabola.
Second-Degree Functions
A parabola is the graph of a second-degree function. That means the variable, usually \(x\), has an exponent of two. The linear equations we learned to graph earlier are first degree, so the \(x\) has an exponent of 1, though it’s usually an invisible exponent because we don’t usually write that little one.
A linear equation is most often found in slope-intercept form, like this:
We can even write it with the exponent so we can see the “first degreeness” of the equation:
It’s the same thing, and though it’s a bit confusing to have an invisible exponent, we should be glad we don’t have to write that little 1 every time we write a variable that is first degree! Here’s an example of a second degree function:
Function Notation
Notice that our \(y\) turned into an \(f\) of \(x\). This is called function notation and it looks a lot more complicated than it really is. It’s just a way for us to keep track of our functions when we have more than one, such as when we have systems of equations.
We can use \(f\) of \(x\) instead of \(y\) with linear equations too but most of us didn’t learn function notation until after we learned linear equations so we’re more accustomed to the \(y\).
Okay, let’s get back to second degree functions. One thing we definitely need to know is that they are often called quadratic functions. So whenever we hear “quadratic function” we need to remember that means second degree, which means the highest exponent on the variable is a 2.
Standard Form of a Quadratic Function
Now compare this to the standard form of a quadratic function, which looks like this:
In this form \(a\), \(b\), and \(c\) are constants, which means they are numbers. In our example, \(a = 1\), \(b = 2\) and \(c = -3\). Notice that the coefficient of our \(x^{2}\)-term is invisible because it is a 1. This is very common with quadratic functions, so we need to remember that whenever we can’t see our a it’s because it’s another one of those invisible 1s.
Graphing
Being able to identify our \(a\), \(b\), and \(c\) are very important for finding the most important points on the parabola so we can graph it efficiently. It is true that we could graph our quadratic by finding points on the curve by plugging in values for \(x\) and getting our \(y\)-values. The problem is that it’s not always easy to find the top or bottom that way. Here is a graph of our sample function with the most important points highlighted:
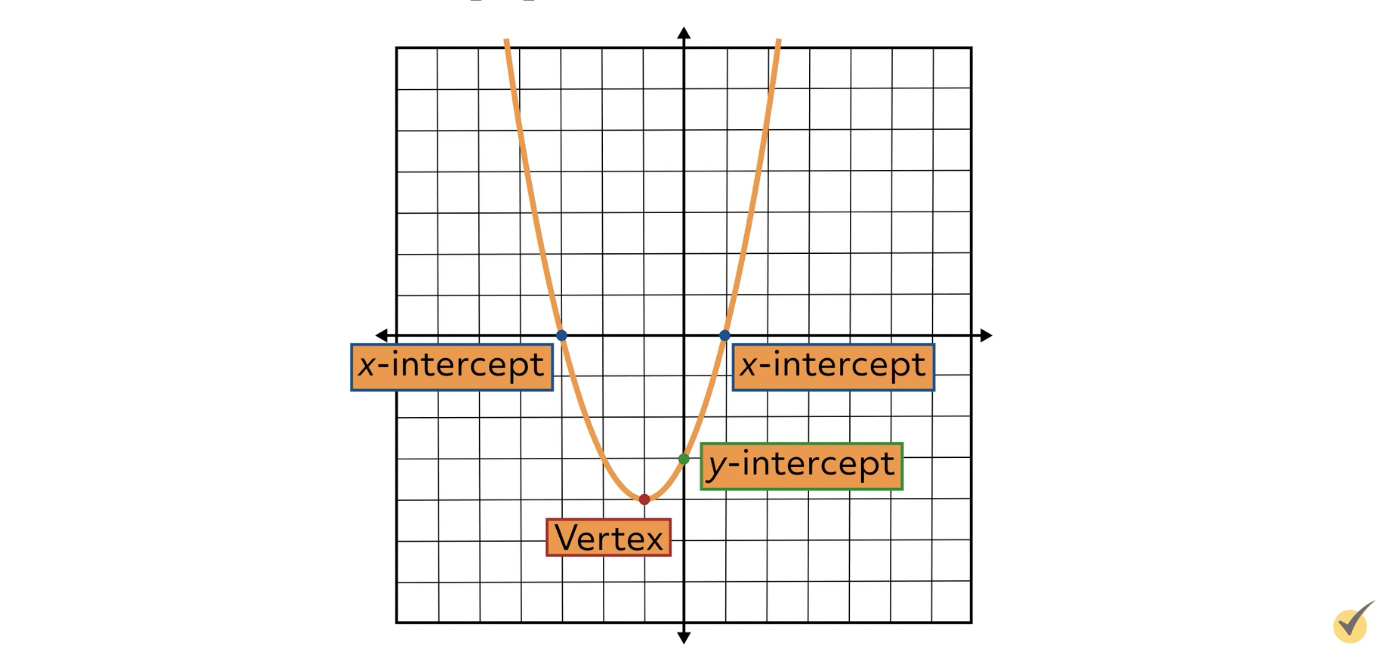
The \(x\)-intercepts are sometimes called “roots” and can be found by factoring, completing the square, and the quadratic formula. The \(y\)-intercept is easily found when a quadratic function is in standard form – it’s the \(c\)! In our example \(c = -3\) and on our graph we can see that our \(y\)-intercept takes place at the point \((0,-3)\).
The Vertex
The last point is the vertex, which might just be the most important point on any parabola. The vertex is either the top or the bottom of a parabola, depending on which way it’s facing. For our example, the vertex is the bottom of the parabola. We can easily find its location on the graph, but how do we find it when we only have the function and not the graph? We start by noticing something important about parabolas in general – they are symmetrical!
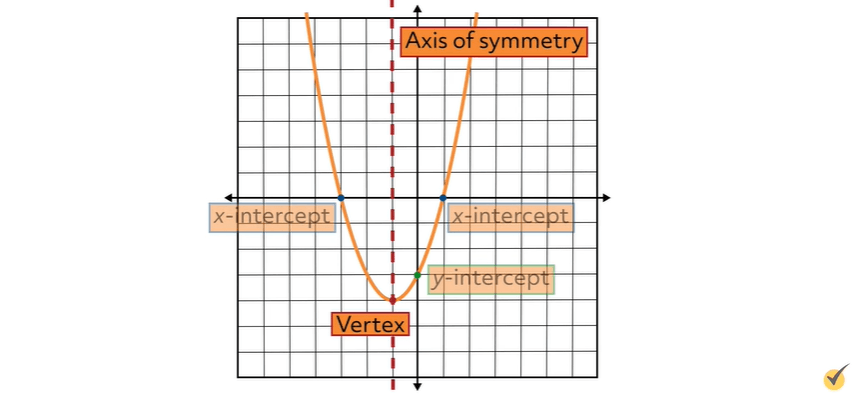
The Axis of Symmetry
We can see the axis of symmetry shown as a red dashed line and can imagine folding our graph on this line and holding up our paper to the light so we can see the two halves of the parabola overlapping each other. Perfect symmetry.
This axis of symmetry can be found using our \(a\), \(b\), and \(c\). Well, we don’t really need \(c\) but since we already used it to find the \(y\)-intercept, it won’t feel left out. Here’s the formula for finding the axis of symmetry:
Remember that when we have an equation written as “\(x\) equals a number” it is an equation of a vertical line. That’s what we’re trying to find here.
Let’s take a look at our sample function again so we can find \(a\), \(b\), and \(c\):
Remembering that \(a\), \(b\), and \(c\) are shown, or not shown if invisible, from left to right and we can find \(a = 1\), \(b = 2\), and \(c = -3\). Now we can plug \(a\) and \(b\) into our formula for axis of symmetry:
| \(x=\frac{-b}{2a}\) | Formula for axis of symmetry |
| \(x=\frac{-(2)}{2(1)}\) | Substitute values of \(a\) and \(b\) using parentheses |
| \(x=\frac{-2}{2}\) | Evaluate numerator and denominator |
| \(x=-1\) | Simplify |
Now we see that our axis of symmetry is the line \(x = –1\), just like on our graph.
Substitution
Notice that the vertex sits on the axis of symmetry. That means the \(x\)-value of the vertex is the same as the \(x\)-value of any other point on the axis of symmetry. In this case, that means it’s –1. Now we just need to find the \(y\)-value of the vertex. We do that by substituting our \(x\)-value into our function.
\(f(-1)=(-1)^{2}+2\left ( -1 \right )-3\)
\(f(-1)=1+(-2)-3\)
\(f(-1)=-4\)
That’s the \(y\)-value of our vertex! Now we know our vertex is at the point \((-1,-4)\). And that’s exactly where it is shown on our graph.
Vertex Form
So far we’ve been using the standard form of our quadratic function. But there’s another form called vertex form. We can convert from standard form to vertex form by completing the square, which is a whole big process that we don’t actually need for this problem since we already found the vertex. The coordinates are all we need to write our function in vertex form.
This is what vertex form looks like:
The \(a\) is the same a from standard form, so it just carries over. Remember that the a is invisible for this function because its value is 1. The two new letters \(h\) and \(k\) are simply the \(x\)– and \(y\)-values of the vertex! Since our vertex for this problem is the point \((-1,-4)\) that means that \(h=-1\) and \(k =-4\).
Now we can substitute the values for \(a\), \(h\), and \(k\) into our general vertex form equation:
Notice that we have a “subtracting a negative” situation happening inside the parentheses. When this happens, the two negatives cancel each other out and become a plus sign.
Just like with our standard form, we don’t have to write the \(a\) if it’s a 1, though it’s certainly not wrong if we do write it. Just know that it won’t usually appear so the equation will probably look like this:
So far we’ve found the vertex from a quadratic in standard form. How is the process different when our function is presented in vertex form? Let’s try a new problem.
Here’s another quadratic function:
Our goal is to find the vertex. Since our function is in vertex form, we just need to identify \(h\) and \(k\). The key is to be careful with the signs. Here’s our general vertex form equation again:
Before we extract our \(h\) and \(k\), we need to make sure our signs are correct. There should be a subtraction sign inside our parentheses and a plus sign after it. In our function, the subtraction sign is right but the plus sign isn’t:
But that’s okay, we can simply rewrite the subtraction as adding a negative:
Now that we have our signs correct we can see that \(h = 3\) and \(k = –7\), so our vertex is \((h,k)\) which is \((3,–7)\). In this type of problem, we don’t need to find our axis of symmetry before finding the vertex. If we want to know the equation for our axis of symmetry, we can find it from the vertex since the \(h\) gives us the value for our vertical line equation: \(x=h\) so \(x=3\) for this function.
Real-World Problems
So how is all of this useful? A lot of real world events can be modeled with quadratic functions. Gravity problems are the most common. Let’s try one:
A football player punts a football, and the height of the football in feet is modeled by the function \(f(x)=-16(x-2)^{2}+53\), where \(x\) is the time in seconds. Question 1: How long does it take for the football to reach its maximum height? Question 2: What is the maximum height of the football?
The function is written in vertex form. The \(a\) for the function is -16. But we don’t need a to solve this problem. All we need to know to answer the two questions is the coordinates of the vertex. Let’s check our signs. Remember, when our equation is in vertex form, we want to subtract our \(h\) value and add our \(k\) value. When looking at our equation for our football, we see that our signs are correct as written.
\(f(x)=-16(x-3)^{2}+53\)
So now we can extract our \(h\) and \(k\).
We see that \(h=3\) and \(k=53\). So the coordinates of the vertex are \((3,53)\). But how does that answer the two questions? The problem states that “\(x\) is time in seconds”. So the \(x\)-value of our vertex is the time it took for the football to reach its maximum height. In this case it took 3 seconds. The function models the height of the football so the \(y\)-value of the vertex is the maximum height, 53 feet! This is what the graph of the function looks like:
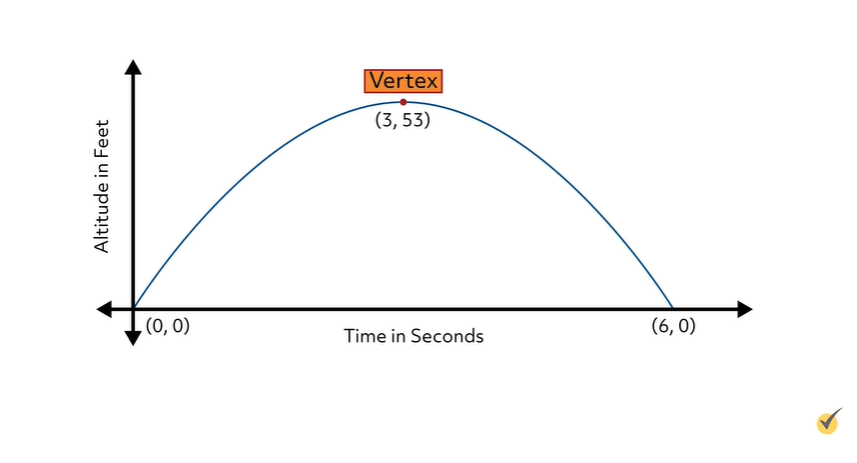
The football starts at 0 seconds and 0 feet, then reaches its maximum height of 53 feet after 3 seconds and finally comes back down to the ground after a total of 6 seconds. We know that because our parabola is symmetrical! So if it took 3 seconds to go up, it took 3 more to come down.
That’s it for the vertex of a parabola. Thanks for watching, and happy studying!
Vertex of a Parabola Practice Questions
Find the vertex of the following quadratic equation: \(f(x)=x^2+6x+11\).
The equation is \(f(x)=x^2+6x+11\) in standard form. The formula \(x=-\frac{b}{2a}\) can be used to determine the \(x\)-coordinate of the vertex of the parabola. In the equation \(f(x)=x^2+6x+11\), \(a=1\), \(b=6\), and \(c=11\). Substitute these values into the formula.
\(x=-\frac{b}{2a}\)
\(x=-\frac{(6)}{2(1)}\)
\(x=-\frac{6}{2}\)
\(x=-3\)
The \(x\)-value of the vertex is –3. Plug this in for \(x\) in the original equation in order to determine the \(y\)-value of the vertex.
\(f(x)=x^2+6x+11\)
\(f(-3)={(-3)}^2+6(-3)+11\)
\(f(-3)=9-18+11\)
\(f(-3)=2\)
When \(x\) is –3, \(y\) is 2. This means the vertex of the parabola is \((-3,2)\).
What is the vertex of the parabola formed by the equation \(f(x)=3x^2+12x+7\)?
The function \(f(x)=3x^2+12x+7\) is in standard form, so we can identify the values of \(a\), \(b\), and \(c\): \(a=3\), \(b=12\), and \(c=7\). These values can be substituted into the vertex formula, \(x=-\frac{b}{2a}\).
\(x=-\frac{b}{2a}\)
\(x=-\frac{12}{2(3)}\)
\(x=-\frac{12}{6}\)
\(x=-2\)
So, –2 is the \(x\)-value of the vertex \((-2,y)\). To find the \(y\)-value of the vertex, plug in –2 for every value of \(x\) in the original equation.
\(f(x)=3x^2+12x+7\)
\(f(-2)=3{(-2)}^2+12(-2)+7\)
\(f(-2)=3(4)+12(-2)+7\)
\(f(-2)=12-24+7\)
\(f(-2)=-5\)
The \(y\)-value of the vertex is –5. The vertex of the parabola is \((-2,-5)\).
Determine the vertex of the following function: \(f(x)=(x+2)^2-1\).
The function \(f(x)=(x+2)^2-1\) is in vertex form. This is convenient because the vertex is expressed within the equation as \(h\) and \(k\). Remember, vertex form is \(f(x)=a(x-h)^2+k\), where \((h,k)\) represents the vertex. In the equation \(f(x)=(x+2)^2-1\), \(h\) is –2, and \(k\) is –1. This means the vertex is \((-2,-1)\).
A football player is attempting to score a field goal. The trajectory of the ball is traced and plotted onto a graph that forms a parabola. The equation of the parabola in vertex form is \(f(x)=-16(x-2)^2+40\), where \(x\) represents the time since the ball was kicked in seconds and \(f(x)\) represents the height of the ball in feet. What was the highest point of the football on its path through the air? Express your answer as an ordered pair and describe the maximum height.
The equation that represents the football’s trajectory is \(f(x)=-16(x-2)^2+40\). The highest point on this parabola is the vertex. To determine the vertex, locate \(h\) and \(k\). Vertex form contains the vertex \((h,k)\) within the equation \(f(x)=a(x-h)^2+k\). In the equation \(f(x)=-16(x-2)^2+40\), \(h\) is 2, and \(k\) is 40. The vertex of the parabola is \((2,40)\). This means that the football’s highest point took place after 2 seconds, at 40 feet.
A bottle rocket’s trajectory through the air creates a parabola when graphed. The equation that expresses the rocket’s path is \(f(x)=-16x^2+64x\), where \(x\) represents time in seconds and \(f(x)\) represents distance in feet. According to the function, how many seconds did it take to reach its highest point? What was the highest point the bottle rocket reached?
The rocket’s path forms a parabola that can be expressed with the equation \(f(x)=-16x^2+64x\). This equation is in standard form, so the \(x\)-coordinate of the vertex can be identified using the formula \(x=-\frac{b}{2a}\). In the equation \(f(x)=-16x^2+64x\), \(a=-16\), \(b=64\), and \(c=0\). Substitute \(a\) and \(b\) into the formula.
\(x=-\frac{b}{2a}\)
\(x=-\frac{64}{2(-16)}\)
\(x=-\frac{64}{-32}\)
\(x=2\)
The variable \(x\) represents time in seconds, so the rocket was at its highest point after 2 seconds. Plug in 2 for \(x\) in order to calculate the height of the rocket.
\(f(x)=-16x^2+64x\)
\(f(2)=-16{(2)}^2+64(2)\)
\(f(2)=-16(4)+64(2)\)
\(f(2)=-64+128\)
\(f(2)=64\)
This means that after 2 seconds the rocket’s height was 64 feet. The vertex of the parabola is \((2,64)\), which is the highest point of the graph.
