
Hi, and welcome to this video about absolute value! We’ll cover what the absolute value of a number is and how to calculate it, as well as what absolute difference is and how it relates to absolute value. Let’s get started!
What is Absolute Value?
The absolute value of a number is its distance from 0 on a number line. Let’s use the number 6 as an example. Using a number line, we can see that 6 is six units away from 0.

Therefore, the absolute value of 6 is 6. Negative 6 is also six units away from 0. The absolute value of – 6 is also 6.

Notation
Absolute value has a specific notation in mathematical expressions. For instance, the absolute value of 6 is denoted with two vertical lines: \(|6|\). And the absolute value of -6 is denoted as -6 with lines on either side, just as before: \(|-6|\).
Absolute Value of Negative Numbers
Now, as we just saw, the absolute value of 6 equals 6 and the absolute value of -6 also equals 6.
No matter what number you are dealing with, big or large, positive or negative, the absolute value operation always yields a positive number. This is good to remember when evaluating expressions and solving equations, but it’s also important to remember why.
When we talk about distance, the direction doesn’t matter. In everyday language, we wouldn’t say, for instance, “The grocery store is negative 1 mile away.” We’d simply say “The grocery store is a mile away.”
Similarly, on the number line, we are simply counting distance without specifying direction. So the absolute value of seven equals seven literally translates to “negative 7 is seven units away from 0.”
When we evaluate expressions and solve equations, the absolute value brackets act very much like parentheses do in the order of operations. We evaluate what’s inside the absolute value brackets first.
Absolute Value Examples
Let’s look at a simple example.
We evaluate what’s inside the brackets first, so 2 plus -5 equals -3, which gives us 1 minus the absolute value of -3. Negative 3 is three units away from zero, which means the absolute value of -3 is 3. This gives us 1 minus 3, which equals -2.
Since absolute value is a calculation of a number’s distance from zero, an absolute value expression such as the absolute value of 3 can be written as the absolute value of 3-0. Another way to interpret this statement is by saying “The distance between 3 and 0 is 3.” Writing it this way provides the same result. The second number here doesn’t need to be 0, though. We can actually calculate the distance between any two numbers.
On a number line, the distance between -2 and 8 is 10. As an expression, we might write it as the absolute value of -2 minus 8 equals 10. This is called an absolute difference.
Let’s do a quick recap. The absolute value of a number is its distance from zero on a number line, and regardless of what number you’re working with, the answer will always be a positive number. The absolute difference is used to calculate the distance between any two numbers on the number line, not just a number and zero.
I hope this review was helpful! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What is absolute value?
A
Absolute value is the distance a number is from zero.
Q
How do you find absolute value?
A
Find the absolute value of a number by determining how far away it is from zero. In other words, make the number positive.
Ex. |-17| = 17
Q
How do you solve absolute value equations?
A
Solve absolute value equations by isolating the absolute value expression and then use both positive and negative answers to solve for the variable. Your variable will most likely equal two different values.
Ex. 2|x – 3| = 14
First, isolate the absolute value expression by dividing both sides by 2.
|x – 3| = 7
Then, solve x – 3 = ±7.
x – 3 = 7
x = 10
Or
x – 3 = -7
x = -4
So x = 10 or x = -4.
Q
How do you solve absolute value inequalities?
A
Solve absolute value inequalities by first manipulating the inequality so that the absolute value expression is isolated on one side. Then, remove the absolute value signs and place the expression between the positive and negative answer. Finally, manipulate to isolate the variable in the middle.
Ex. 4|2x – 3| < 28
|2x – 3| < 7
-7 < 2x - 3 < 7
-4 < 2x < 10
-2 < x < 5
Q
How do you graph absolute value?
A
To graph absolute value equations, first graph the expression inside the absolute value signs. Then, whatever is under the x-axis on that graph, reflect over the x-axis so it is now positive.
Ex. y = |x + 1|
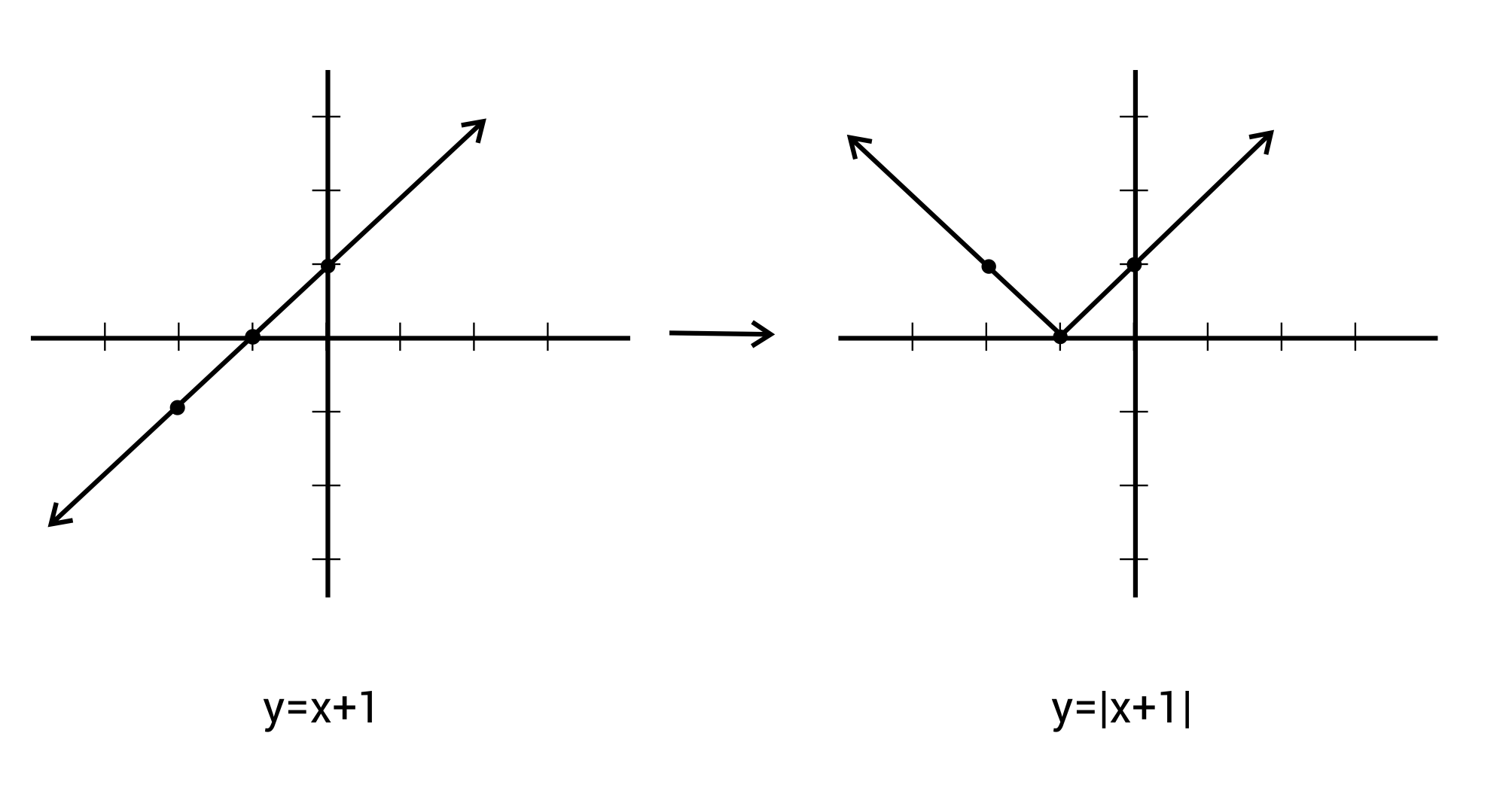
Absolute Value Practice Questions
\(|-2|=\)
The correct answer is 2. Absolute value tells you how far away a number is from 0 so it is always the positive value of a number. \(|-2|=2\) because -2 is 2 positions away from 0.
\(|-3-11|=\)
The correct answer is 14. Absolute value makes any number positive because it tells how far away a number is from 0. First, simplify the expression inside the absolute value bars.
\(|-3-11|=|-14|\)
Then, take the absolute value of -14, \(|-14|=14\).
\(|4-7+8|=\)
The correct answer is 5. Absolute value makes any number positive because it tells how far away it is from 0. First, simplify the expression in the absolute value bars.
\(|4-7+8|=|5|\)
Then, take the absolute value of 5, \(|5|=5\). 5 stays positive because it is 5 positions away from 0.
\(|6-7+2|-9=\)
The correct answer is -8.
\(|6-7+2|-9\)
First, simplify the expression in the absolute value bars.
\(|1|-9\)
Then, take the absolute value of 1.
\(1-9\)
Finally, subtract.
\(1-9=-8\)
\(4-|16+7-35|-21=\)
The correct answer is -29.
\(4-|16+7-35|-21\)
First, simplify the expression in the absolute value bars.
\(4-|-12|-21\)
Then, take the absolute value of -12.
\(4-12-21\)
Finally, subtract.
\(4-12-21=-29\)
