Irrational Numbers on a Number Line
When placing irrational numbers on a number line, note that your placement will not be exact, but a very close estimation. For instance, when placing √15 (which is 3.87), it is best to place the dot on the number line at a place in between 3 and 4 (closer to 4), and then write √15 above it. Writing 3.87 would not be entirely accurate, and you can’t write out every decimal number because it ever ends. This is why √15 is the best thing to write.
Hi, and welcome to this review of irrational numbers! Today, we’ll be reminded of what an irrational number is, and look at where they fall on a number line. Let’s get started!
So, first, what is an irrational number? It is easy to determine whether a number is rational or irrational based on the word itself. Look closely… the root word ratio tells us that these numbers can be written as a fraction.
Rational numbers include all proper and improper fractions. Decimals that repeat or that terminate can be written as fractions, so they are considered rational. For example, .3333333 can be expressed as the fraction, 13, so it is a rational number.
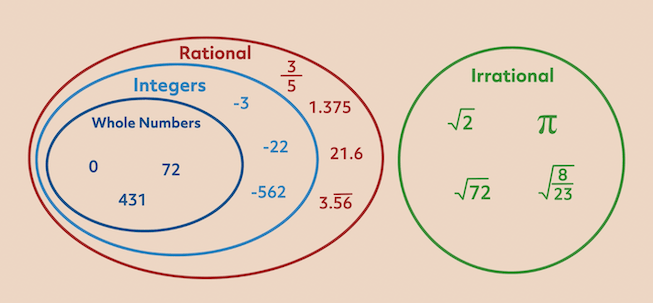
This diagram clearly shows that there is no overlap between the rational and irrational number sets. Another way of thinking about it is that irrational numbers are those that cannot be written as a fraction.
A common example of an irrational number is the value derived from taking the square root of a non-perfect square. That may sound confusing, so let’s look at a few examples to simplify the terminology.
A perfect square is a number that can be re-written as an integer multiplied by itself.
For example, 4 = 2 × 2, or written another way, 4 = 22. This shows that 4 is a perfect square.
Similarly, 16 can be rewritten as 4 × 4, or 42. So, 16 is also a perfect square.
Because taking the square root of a perfect square results in an integer, it can easily be found on a number line. But how do we know where the value \(\sqrt5\) would fall on a number line? Well, \(\sqrt{5}\) = 2.236, so we can guess that it lands somewhere around here on the number line.
Let’s say we had \(\sqrt{31}\). Where would this value fall on a number line?
Thirty-one is not a perfect square. The closest perfect square that is less than 31 is 25, and the closest perfect square greater than 31 is 36. The square roots of 25 and 36 are 5 and 6, respectively, so we know we can place \(\sqrt{31}\) somewhere in between. If we calculate \(\sqrt{31}\), we indeed get 5.567, so we can estimate that it falls halfway between 5 and 6.
There are actually some famous irrational numbers that you may have seen before. Pi, for example, is a non-repeating decimal that goes on for infinity every time… for every circle! When calculating with pi, a common estimate is 3.14159, or the fraction \(\frac{22}{7}\).
Phi is another irrational number that can, at best, be mathematically approximated. The general estimation is the value 1.618, which is used in visual arts, architecture, and design applications.
The math constant, e, is seen frequently in math, and is estimated with the value of 2.71828. This special irrational number is sometimes referred to as Euler’s Number to credit the Swiss mathematician, Leonhard Euler. Formulas dealing with natural logs, complex numbers, and advanced concepts in calculus all use this important irrational number.
So, as you can see, irrational numbers are unique in that they cannot be expressed fully as fractions, but they can be visualized on a number line with rational numbers by using approximations.
Thanks for watching, and happy studying!
Irrational Numbers on a Number Line Practice Questions
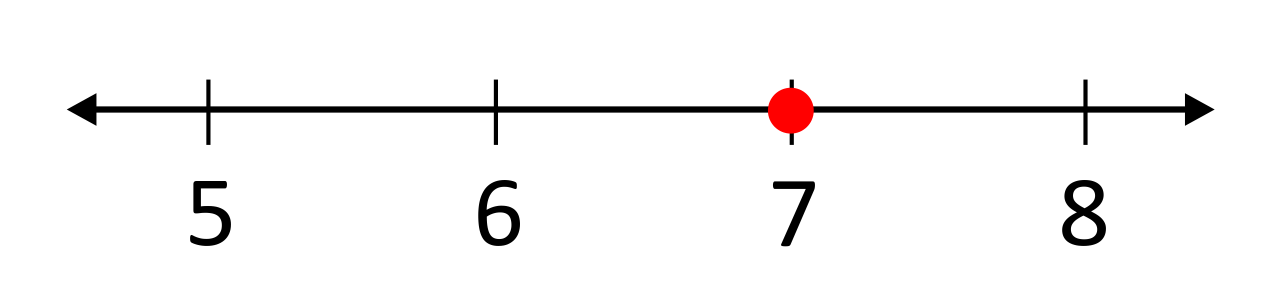
Is the number \(2\pi\) a rational or irrational number? Represent this value using a number line.
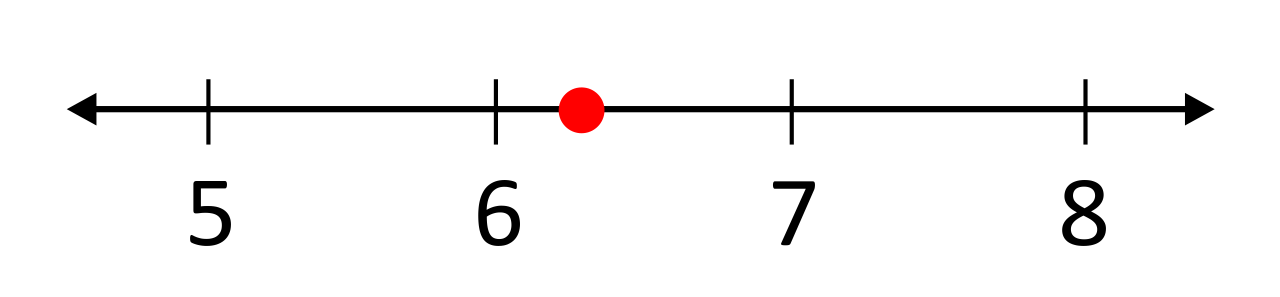
We know that \(π\) is an irrational number because it can’t be written as a fraction with whole numbers in both the numerator and denominator, so \(2π\) is an irrational number as well. Additionally, the value \(2π=6.28318…\) sits between 6 and 7.
Find the two consecutive integers that \(\sqrt{77}\) sits between and build the inequality.
By all means, we could simply plug the value \(\sqrt{77}\) into a calculator and see that \(8\) < \(\sqrt{77}=8.774…\) < \(9\). However, what if we didn’t have access to a calculator? Let’s think about all of the squares we know: \(1,4,9,…64,81,100,…\) Notice that \(64\) < \(77\) < \(81\), so we could also say: \(\sqrt{64}\) < \(\sqrt{77}\) < \(\sqrt{81}\). Hence, \(8\) < \(\sqrt{77}\) < \(9\).
Find the two consecutive integers that border \(2\sqrt{14}\) and build the inequality.
Once again, we could use a calculator to find that \(2\sqrt{14}=7.483…\), but let’s try working this out by hand instead. First of all, notice that \(2\sqrt{14}=\sqrt{4}\times\sqrt{14}=\sqrt{56}\). If we consider simple square values again, we can end up seeing \(7=\sqrt{49}\) < \(\sqrt{56} < \sqrt{64}=8\).
Represent the irrational number \(\frac{26.7}{7.21}\) on a number line.
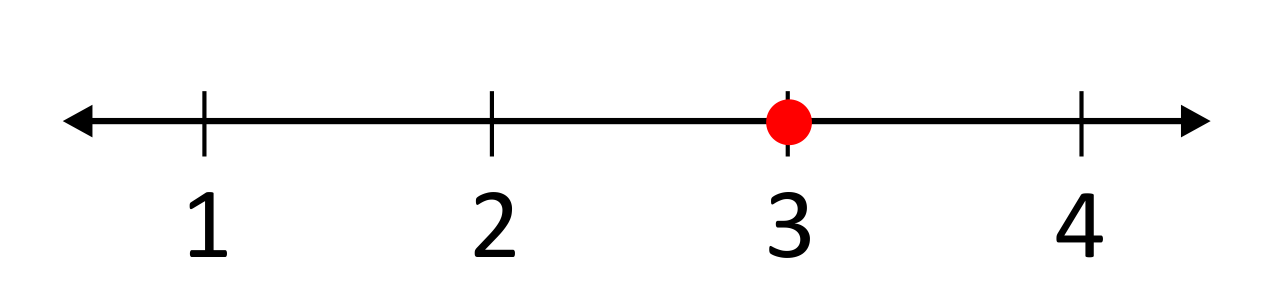
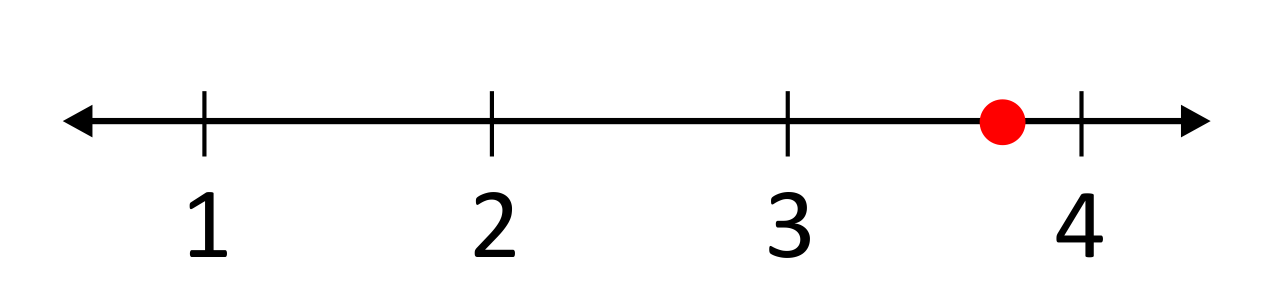
If you divide this fraction on a calculator, you will find that it is equal to 3.7031… But what would you do if you didn’t have a calculator? There are multiple different ways to approach this problem. One way is to consider the factors of 7: 7, 14, 21, 28, 35, . . . 26.7 falls between 21 and 28, so it can be assumed that \(\frac{21}{7.21}\approx3\) and \(\frac{28}{7.21}\approx4\), so \(\frac{26.7}{7.21}\) must be between 3 and 4.
Represent the irrational number \(\frac{5e}{2}\) on a number line.
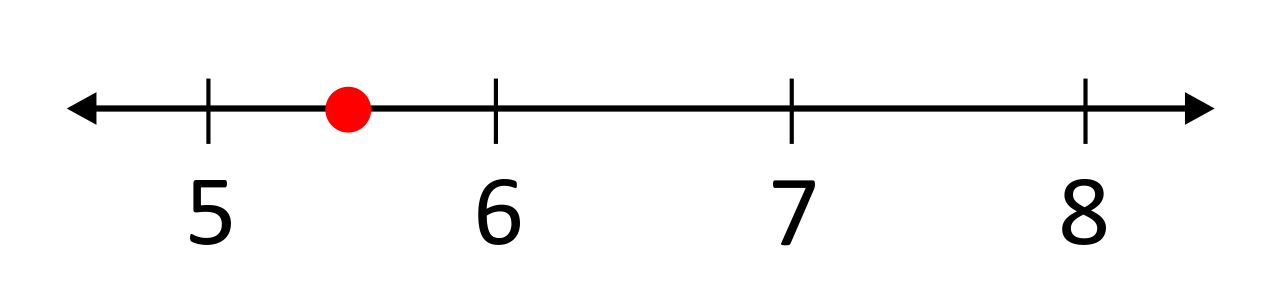
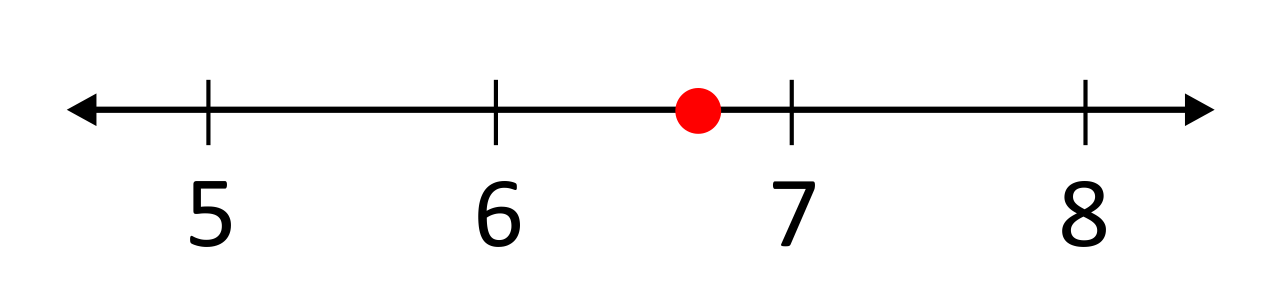
Plugging this value into a calculator will result in 6.7957, which would graph the point between 6 and 7.
