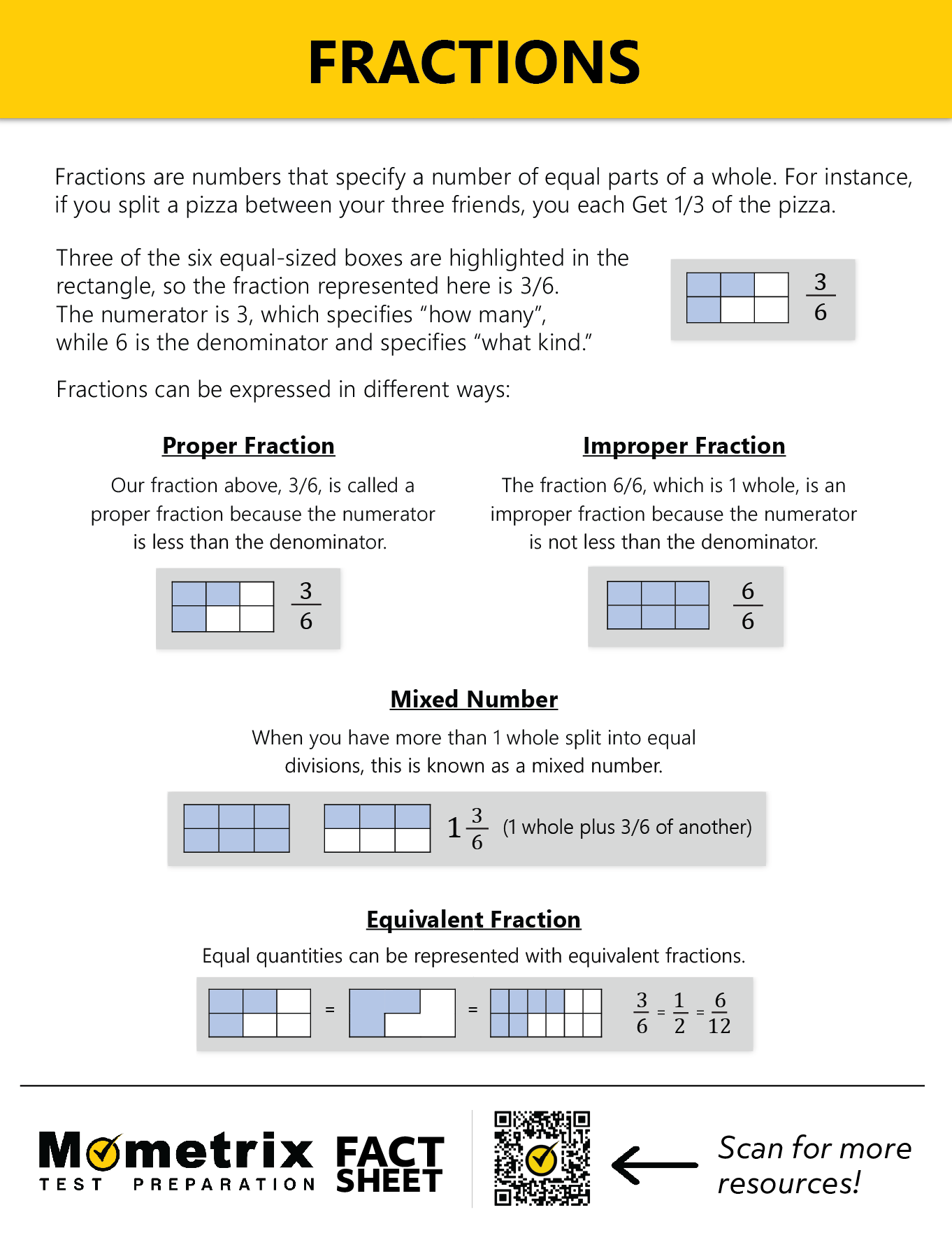
Overview of Fractions

Hey guys, welcome to this Mometrix video on fractions. Fractions can be simple or complex. In this video, we’ll cover different types of fractions and how to add fractions with different denominators.
What is a Fraction?
So, what is a fraction? A fraction is a part of a whole, which means a fraction can never be a whole number. Think of it like this:
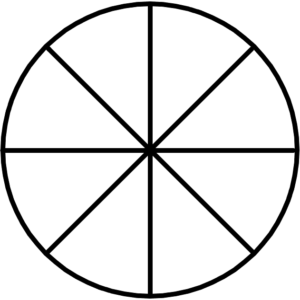
Our circle is divided into eight equal pieces. Let’s say three pieces were filled in.
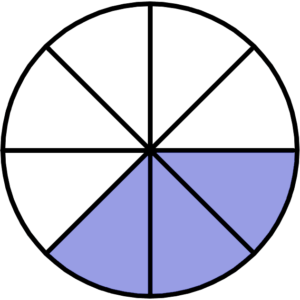
That means that \(\frac{3}{8}\) of our circle is filled in. The top number (3) is called the numerator. The bottom number of a fraction is called the denominator (8, in this case). When saying fractions out loud, the denominator will usually be spoken as the ordinal version of the number. You would say “eighth” instead of “eight,” or “third” instead of “three.”
Let’s take a look at a list of our denominators and see how we would say them.
2 = half
3 = third
4 = fourth or quarter
5 = fifth
6 = sixth
7 = seventh
8 = eighth
9 = ninth
10 = tenth
As you can see, there are a couple of exceptions. If our denominator is 2, you can say “half” instead of “second,” or if our denominator is 4, you could say “quarter” instead of “fourth;” either one is acceptable. Hopefully, that helps you to understand how fractions are defined, and also how to actually say them out loud. But there are different types of fractions. Let’s take a look at those.
Proper Fractions
First, we have a proper fraction. A proper fraction always has a numerator (which we looked at) that is smaller than the denominator. Our example that we used before, \(\frac{3}{8}\), so our numerator, 3, is smaller than our denominator, 8. Some other examples of proper fractions include \(\frac{4}{5}\), \(\frac{5}{9}\), and \(\frac{23}{50}\). An improper fraction is the opposite of a proper fraction, in that the numerator is larger than the denominator. So, while \(\frac{3}{8}\) is a proper fraction, \(\frac{8}{3}\) is an improper fraction because the numerator is larger than our denominator. Improper fractions are always equal to or greater than 1. That means \(\frac{9}{9}\) is an improper fraction since it’s equal to 1. There are also mixed fractions, which contain a whole number and a proper fraction. Here’s an example: 2\(\frac{3}{4}\). Note that the whole number, 2, is followed by the proper fraction, \(\frac{3}{4}\).
Equivalent Fractions
We also have equivalent fractions. Equivalent fractions are two different fractions that name the same number. For example: \(\frac{6}{8}\) and \(\frac{3}{4}\) look different, but they’re the same. \(\frac{3}{4}\) is just a simplified, or reduced, version of \(\frac{6}{8}\). To simplify \(\frac{6}{8}\), you just divide the numerator and the denominator by 2 to get \(\frac{3}{4}\). Now that we know the different types of fractions, we can explore how to add them. If two fractions have the same denominator, adding is a breeze. You just add the numerators together, and that gives you the answer. For example: \(\frac{1}{4} + \frac{2}{4} = \frac{3}{4}\)
Adding Fractions with Different Denominators
So notice what we did to get \(\frac{3}{4}\). All we had to do was add, from our first fraction the 1 from our numerator, and from our second fraction the 2 from our numerator. Add them together to get 3, and just bring over our 4 from the denominator. Simple. But what happens if the denominators are different? Well, in that case, you have to convert the denominators to be the same. So let’s take a look at an example: \(\frac{3}{8} + \frac{1}{2} = x\)
You can’t really simplify \(\frac{3}{8}\) into anything that would easily add with \(\frac{1}{2}\), but we can do something with \(\frac{1}{2}\) that we can easily add with \(\frac{3}{8}\), and that’s multiplying 2 by 4, which would give us 8. But whatever we do to our denominator, we also have to do to our denominator. So that would look like this: \(\frac{3}{8} + \frac{1\times 4}{2\times 4} = x\)
So our equation now becomes: \(\frac{3}{8} + \frac{4}{8} = \frac{7}{8}\)
Subtracting Fractions with Different Denominators
Subtraction works the same way. If you’re subtracting fractions with the same denominator, you can just subtract the top numbers, like in this example: \(\frac{3}{4} – \frac{1}{4} = \frac{2}{4} = \frac{1}{2}\)
So in this example, all we had to do was subtract our top numerators here, to give us \(\frac{2}{4}\), which simplifies to \(\frac{1}{2}\). Simplifying numbers just makes them easier to work with. But if you’re subtracting with a different denominator, you have to make the denominators match. For example: \(\frac{3}{8} – \frac{1}{4} = x\)
So in this example, \(\frac{3}{8} – \frac{1}{4} = x\), we are kinda looking at the same issue like we did over here (\(\frac{3}{8} + \frac{1}{2} = x\)), we need our denominators to match. So we need to find out, what can we do to make our denominators match? Well in this case, we can multiply \(4\times 2\), but remember we have to do the same thing that we did to the denominator, we must do to our numerator. So we multiply it by 2 and then here’s what we get: \(\frac{3}{8}-\frac{1\times 2}{4\times 2}=\frac{3}{8} – \frac{2}{8} = \frac{1}{8}\)
So once we multiply our second fraction here by 2, we get \(\frac{3}{8} – \frac{2}{8} = \frac{1}{8}\). So these problems were pretty easy because they had either the same denominator or were easy to convert.
Finding the Least Common Denominator
But let’s look at one more equation that’s a little trickier: \(\frac{3}{4} + \frac{6}{7}\)
So at first glance, it doesn’t look like these numbers have much in common such that we would be able to multiply or divide 4 by anything to get 7, or 7 by anything to get 4. So a lot of the times when you have problems like this, what you end up having to do is multiply this fraction (\(\frac{3}{4}\)) by the denominator of the other fraction. And likewise, we would multiply this fraction (\(\frac{6}{7}\)) by the denominator of this fraction (\(\frac{3}{4}\)). So here’s what that looks like: \(\frac{3 \times 7}{4 \times 7} + \frac{6 \times 4}{7 \times 4}=\frac{21}{28} + \frac{24}{28}\)
So after multiplication, we end up getting a common denominator, which is 28. So now all we have to do is add our numerators together, which that gives us: \(\frac{21}{28} + \frac{24}{28} = \frac{45}{28}\)
And that’s our answer! With this calculation, we found the least common denominator. The least common denominator is the smallest common number between denominators. Any time you perform a calculation with different denominators, you must find the least common denominator to solve the problem. So that’s our look at fractions.
I hope this video was helpful to you!
For more help, check out our fractions calculator!
Frequently Asked Questions
Q
What are the 3 types of fractions?
A
The three types of fractions are: proper fractions, improper fractions, and mixed numbers.
A proper fraction is a fraction whose numerator is less than its denominator, like \(\frac{2}{5}\).
An improper fraction is a fraction whose numerator is greater than its denominator, like \(\frac{5}{2}\).
A mixed number is a fraction that has a whole number part and a proper fraction part, like \(3\frac{1}{5}\).
Q
What are fractions?
A
Fractions are numbers that represent part of a whole.
Q
What is an improper fraction?
A
An improper fraction is a fraction whose numerator is greater than its denominator. It represents a number greater than 1.
Examples:\(\frac{7}{2}\),\(\frac{14}{11}\),\(\frac{9}{5}\),\(\frac{17}{6}\)
Q
How do you know fractions are similar?
A
You can know if fractions are similar or not by looking at their denominators. If they have the same denominator, then they are similar. If they do not have the same denominator, they are not similar.
Similar Fractions: \(\frac{1}{4}\) and \(\frac{3}{4}\)
Unsimilar Fractions: \(\frac{1}{3}\) and \(\frac{1}{5}\)
Q
How do you describe a fraction in words?
A
To write a fraction in words, write the numerator, then a hyphen, then the denominator as an ordinal number (like it’s a place in line).
Ex. \(\frac{3}{4}=\) three-fourths
\(\frac{7}{11}=\) seven-elevenths
Q
How do I write fractions?
A
Write fractions by placing the part over the whole, like this: \(\frac{\text{part}}{\text{whole}}\)
Ex. I have eaten 2 of the 7 cookies. What is this represented as a fraction?
The part I’ve eaten is 2. The whole amount of cookies is 7. So the fraction that represents the amount of cookies I’ve eaten is \(\frac{2}{7}\).
Types of Fractions with Examples PDF
Fraction Problems
Which of the following is an improper fraction?
The correct answer is \(\frac{21}{8}\). An improper fraction is a fraction whose numerator is greater than its denominator.
Which of the following fraction is equivalent to \(\frac{6}{8}\)?
The correct answer is \(\frac{3}{4}\). Equivalent fractions are fractions that name the same number. \(\frac{6}{8}\) is the same as \(\frac{3}{4}\) because dividing both the numerator and denominator by \(\frac{6}{8}\) by 2 results in \(\frac{3}{4}\).
\(\frac{2}{12}+\frac{7}{12}=\)
To add fractions with the same denominator, simply add the numbers in the numerators and keep the denominator the same. \(2+7=9\), so \(\frac{2}{12}+\frac{7}{12}=\frac{9}{12}\).
\(\frac{5}{6}-\frac{2}{3}=\)
The correct answer is \(\frac{1}{6}\). To subtract fractions, first convert them to fractions with the same denominator. \(\frac{2}{3}\) can be converted to \(\frac{4}{6}\) by multiplying both the numerator and denominator by 2.
\(\frac{5}{6}-\frac{4}{6}\)
Then, subtract the numerators and keep the denominator the same. \(5-4=1\), so \(\frac{5}{6}-\frac{4}{6}=\frac{1}{6}\).
\(\frac{3}{7}+\frac{2}{5}=\)
The correct answer is \(\frac{29}{35}\). To add fractions, first convert them to fractions with the same denominator. This can be done by multiplying \(\frac{3}{7}\) by \(\frac{5}{5}\) and \(\frac{2}{5}\) by \(\frac{7}{7}\).
\(\frac{3}{7}\times\frac{5}{5}+\frac{2}{5}\times\frac{7}{7}\)
\(\frac{15}{35}+\frac{14}{35}\)
Then, add the numerators and keep the denominator the same. \(15+14=29\), so \(\frac{15}{35}+\frac{14}{35}=\frac{29}{35}\).
Fraction Worksheets
Use our free printable fraction worksheets for additional practice! We’ve provided equivalent fractions worksheets, dividing fractions worksheets, multiplying fractions worksheets, and adding and subtracting fractions worksheets, all available to download for free.