
Hi, and welcome to this video covering the least common multiple and the greatest common factor!
As you know, there are times when we have to algebraically “adjust” how a number or an equation appears in order to proceed with our math work. We can use the greatest common factor and the least common multiple to do this.
The greatest common factor (GCF) is the largest number that is a factor of two or more numbers, and the least common multiple (LCM) is the smallest number that is a multiple of two or more numbers.
Adding Fractions
To see how these concepts are useful, let’s look at adding fractions. Before we can add fractions, we have to make sure the denominators are the same by creating an equivalent fraction:
In this example, the least common multiple of 3 and 6 must be determined. In other words, “What is the smallest number that both 3 and 6 can divide into evenly?” With a little thought, we realize that 6 is the least common multiple, because 6 divided by 3 is 2 and 6 divided by 6 is 1. The fraction \(\frac{2}{3}\) is then adjusted to the equivalent fraction \(\frac{4}{6}\) by multiplying both the numerator and denominator by 2. Now the two fractions with common denominators can be added for a final value of \(\frac{5}{6}\).
Finding the Least Common Multiple
In the context of adding or subtracting fractions, the least common multiple is referred to as the least common denominator.
In general, you need to determine a number larger than or equal to two or more numbers to find their least common multiple.
It is important to note that there is more than one way to determine the least common multiple. One way is to simply list all the multiples of the values in question and select the smallest shared value, as seen here:
\(8\rightarrow 8,16,24,32,40,48\)
\(4\rightarrow 4,8,12,16,20,24,28,32\)
\(6\rightarrow 6,12,18,24,30,36\)
This illustrates that the least common multiple of 8, 4, and 6 is 24 because it is the smallest number that 8, 4, and 6 can all divide into evenly.
Another common method involves the prime factorization of each value. Remember, a prime number is only divisible by 1 and itself.
Once the prime factors are determined, list the shared factors once, and then multiply them by the other remaining prime factors. The result is the least common multiple:
\(90=2\times 3\times 3\times 5\)
\(\text{LCM}=2\times 3\times 3\times 2\times 5\)
The least common multiple can also be found by common (or repeated) division. This method is sometimes considered faster and more efficient than listing multiples and finding prime factors. Here is an example of finding the least common multiple of 3, 6, and 9 using this method:
Divide the numbers by the factors of any of the three numbers. 6 has a factor of 2, so let’s use 2. You cannot divide 9 and 3 by 2, so we’ll just rewrite 9 and 3 here. Repeat this process until all of the numbers are reduced to 1. Then, multiply all of the factors together to get the least common multiple.
| 2 | 3 | 6 | 9 |
| 3 | 3 | 3 | 9 |
| 3 | 1 | 1 | 3 |
| 1 | 1 | 1 |
LCM \(=2\times 3\times 3=18\)
Now that methods for finding least common multiples have been introduced, we’ll need to change our mindset to finding the greatest common factor of two or more numbers. We will be identifying a value smaller than or equal to the numbers being considered. In other words, ask yourself, “What is the largest value that divides both of these numbers?” Understanding this concept is essential for dividing and factoring polynomials.
What is the Greatest Common Factor?
Prime factorization can also be used to determine the greatest common factor. However, rather than multiplying all the prime factors like we did for the least common multiple, we will multiply only the prime factors that the numbers share. The resulting product is the greatest common factor.
Review
Let’s wrap up with a couple of true or false review questions:
1. The least common multiple of 45 and 60 is 15.
2. The least common multiple is a number greater than or equal to the numbers being considered.
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you find the LCM and GCF?
A
There are a variety of techniques for finding the LCM and GCF. The two most common strategies involve making a list, or using the prime factorization.
For example, the LCM of 5 and 6 can be found by simply listing the multiples of \(5\) and \(6\), and then identifying the lowest multiple shared by both numbers.
\(5, 10, 15, 20, 25, \mathbf{30}, 35…\)
\(6, 12, 18, 24, \mathbf{30}, 36…\)
\(\mathbf{30}\) is the LCM.
Similarly, the GCF can be found by listing the factors of each number, and then identifying the greatest factor that is shared. For example, the GCF of \(40\) and \(32\) can be found by listing the factors of each number.
\(40\): \(1, 2, 4, 5, \mathbf8, 10, 20, 40\)
\(32\): \(1, 2, 4, \mathbf8, 16, 32\)
\(\mathbf8\) is the GCF.
For larger numbers, it will not be realistic to make a list of factors or multiples to identify the GCF or LCM. For large numbers, it is most efficient to use the prime factorization technique.
For example, when finding the LCM, start by finding the prime factorization of each number (this can be done by creating a factor tree). The prime factorization of \(20\) is \(2\times2\times5\), and the prime factorization of \(32\) is \(2\times2\times2\times2\times2\). Circle the factors that are in common and only count these once.
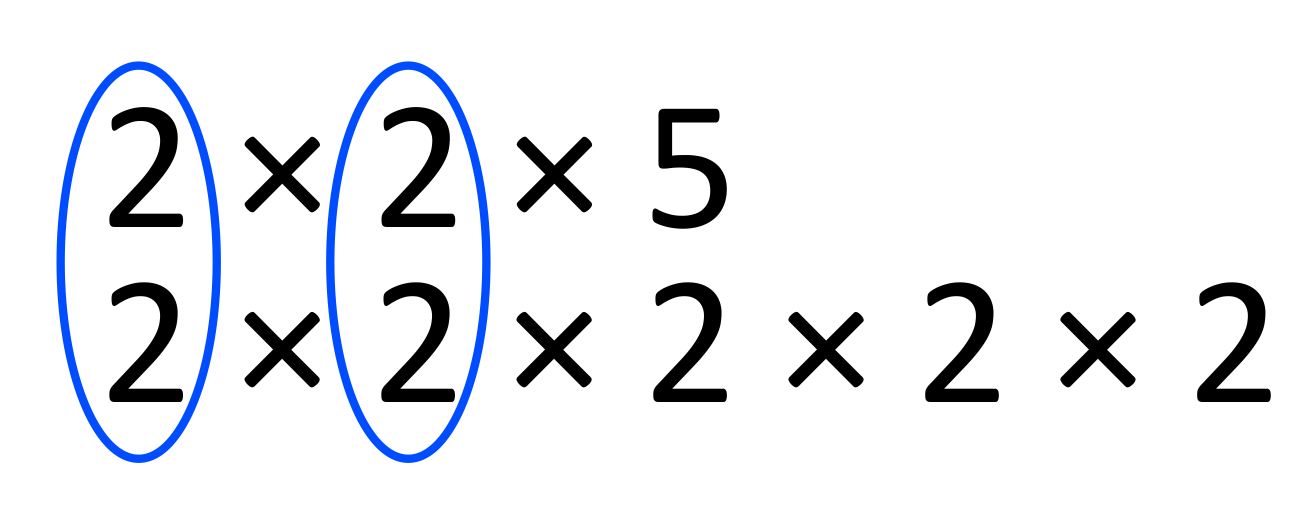
Now multiply all of the factors (remember not to double-count those circled \(2\)s). This becomes \(2\times2\times5\times2\times2\times2\), which equals \(160\). The LCM of \(20\) and \(32\) is \(160\).
When finding the GCF, start by listing the prime factorization of each number (this can be done by creating a factor tree). For example, the prime factorization of \(45\) is \(5\times3\times3\), and the prime factorization of \(120\) is \(5\times3\times2\times2\times2\). Now simply multiply all of the factors that are shared by both numbers. In this case, we would multiply \(5\times3\) which equals \(15\). The GCF of \(45\) and \(120\) is \(15\).
The prime factorization approach can seem like a fairly lengthy process, but when working with large numbers it is guaranteed to be a time-saver.
Q
How do you find the GCF?
A
There are two main strategies for finding the GCF: Listing the factors, or using the prime factorization.
The first strategy involves simply listing the factors of each number, and then looking for the greatest factor that is shared by both numbers. For example, if we are looking for the GCF of \(36\) and \(45\), we can list the factors of both numbers and identify the largest number in common.
\(36\): \(1,2,3,4,6,\mathbf9,12,18,36\)
\(45\): \(1,3,5,\mathbf9,15,45\)
The GCF of \(36\) and \(45\) is \(\mathbf9\).
Listing the factors of each number and then identifying the largest factor in common works well for small numbers. However, when finding the GCF of very large numbers it is more efficient to use the prime factorization approach.
For example, when finding the GCF of \(180\) and \(162\), we start by listing the prime factorization of each number (this can be done by creating a factor tree). The prime factorization of \(180\) is \(2\times2\times3\times3\times5\), and the prime factorization of \(162\) is \(2\times3\times3\times3\times3\). Now look for the factors that are shared by both numbers. In this case, both numbers share one \(2\), and two \(3\)s, or \(2\times3\times3\). The result of \(2\times3\times3\) is \(18\), which is the GCF! This strategy is often more efficient when finding the GCF of really large numbers.
Q
What does GCF mean?
A
The GCF stands for the “greatest common factor”. The GCF is defined as the largest number that is a factor of two or more numbers. For example, the GCF of \(24\) and \(36\) is \(12\), because the largest factor that is shared by \(24\) and \(36\) is \(12\). \(24\) and \(36\) have other factors in common, but \(12\) is the largest.
Q
How do you find the lowest common multiple?
A
There are a variety of techniques for finding the lowest common multiple. Two common approaches are listing the multiples, and using the prime factorization. Listing the multiples is just as it sounds, simply list the multiples of each number, and then look for the lowest multiple shared by both numbers. For example, when finding the lowest common multiple of \(3\) and \(4\), list the multiples:
\(3\): \(3,6,9,\mathbf{12},15,18…\)
\(4\): \(4,8,\mathbf{12},16,20…\)
\(\mathbf{12}\) is the lowest multiple shared by \(3\) and \(4\).
Listing the multiples is a great strategy when the numbers are fairly small. When numbers are large, such as \(38\) and \(42\), we should use the prime factorization approach. Start by listing the prime factorization of each number (this can be done using a factor tree).
\(38\): \(2\times19\)
\(42\): \(2\times3\times7\)
Now circle the shared factors (only count these once).
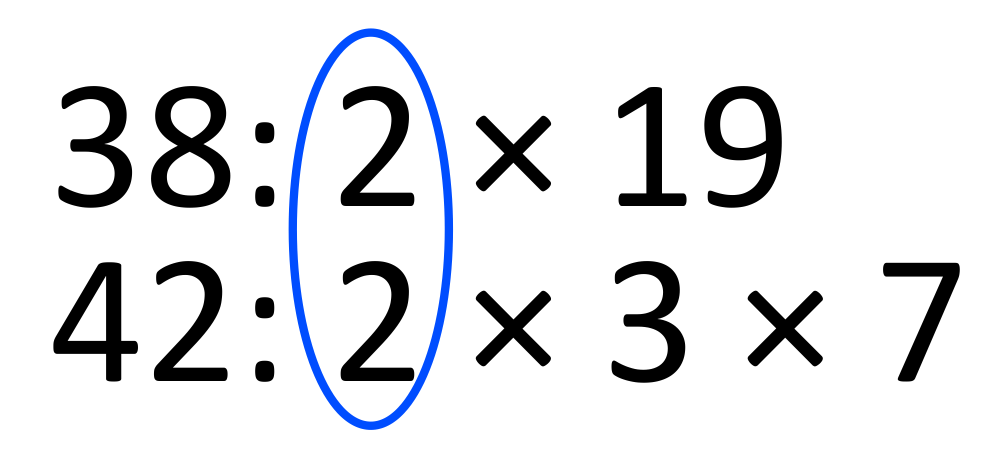
Now multiply all of the factors (remember to only count the \(2\)s once). This becomes \(2\times19\times3\times7\), which equals \(798\). The LCM of \(38\) and \(42\) is \(798\).
Q
How do you take out the LCM?
A
Taking out the LCM is a helpful skill when adding or subtracting fractions. Determining the lowest common multiple creates a denominator that is the same for both fractions. For example, the common denominator for \(\frac{2}{7}+\frac{3}{5}\) would be \(35\), because \(35\) is the LCM of \(7\) and \(5\). The new fractions become \(\frac{10}{35}+\frac{21}{35}\), which equals \(\frac{31}{35}\).
Greatest Common Factor and Least Common Multiple PDFs
Greatest Common Factor and Least Common Multiple Practice Questions
What is the greatest common factor of 16 and 42? Use it to reduce the fraction \(\frac{16}{42}\).
The correct answer is D: GCF is 2, and we reduce to \(\frac{8}{21}\).
Let’s approach this problem by listing the prime factors of both the numerator and the denominator.
\(16=2×2×2×2\)
\(42=2×3×7\)
Here we see that 2 is the only shared factor of 16 and 42 and is therefore their greatest common factor. We can then divide both numbers by 2 to reduce the fraction:
\(\frac{16\div2}{42\div2}=\frac{8}{21}\)
Find the least common multiple of 2, 6, and 8.
The correct answer is C: 24.
For this problem, let’s list the prime factors of each number.
\(2=2\) (note that we could write \(2\times1\), but 1 is understood, or implied, and usually not necessary to write)
\(6=2\times3\)
\(8=2\times2\times2\)
Remember, when calculating the LCM of two or more numbers, we list each prime factor once that is shared by all of the numbers. Since each of our numbers has 2 as a prime factor, our LCM will also have 2 as one of its prime factors.
LCM \(=2\times\) _______.
Now from the 6 we have a leftover 3, and from the 8 we have two 2’s remaining. We multiply those in to get LCM \(=2\times3\times2\times2=24\).
Notice that even though 2, 6, and 8 are all factors of 48, the solution is not D, because 48 is not the smallest common multiple.
List the first several multiples of 3, 5, and 6 to find the least common multiple.
The correct answer is B: LCM is 30.
The first several multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, …
The first several multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …
The first several multiples of 6 are: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
As we see above, 30 is the first (least) number that 3, 5, and 6 have in common among their multiples, so the least common multiple is 30.
Courtney has 54 pieces of candy, and Trish has 36. They want to prepare goodie bags of candy for their friend Kim’s birthday party, but each bag needs to have an equal amount of candy. In order to have the most candy in each bag, with Courtney and Trish working separately, how many bags can they make, and how much candy will be in each bag?
The correct answer is D: 5 bags, with 18 pieces of candy in each.
To begin, list the prime factors of both 54 and 36:
\(54=2\times3\times3\times3\)
\(36=2\times2\times3\times3\)
Notice that they both share a 2 and two 3s. The product of these shared prime factors is \(2\times3\times3=18\). We now know that the GCF is 18, which means each bag will contain 18 pieces of candy. Courtney’s 54 pieces will make 3 bags, and Trish’s 36 pieces will make 2 bags. Together, they will make 5 bags with 18 pieces of candy in each.
Sara is buying fruit for an office brunch, and she needs an equal number of apples and bananas. However, the apples are sold in bags of 4 and the bananas are sold in bunches of 6. What is the least number of apples and bananas Sara can buy?
The correct answer is C: 12 apples and 12 bananas.
With this problem, we want to know the least common multiple of 4 and 6. Using the prime factors method, we see the following:
\(4=2\times2\)
\(6=2\times3\)
LCM \(=2\times2\times3=12\)
Sara will buy three bags of apples and two bunches of bananas in order to have 12 of each fruit.



