Mometrix’s pre-algebra videos are general reviews of the concepts, ideas, and topics that may be presented on an exam. Each of these videos will give a wide-scope review of what a test taker may need to know as they prepare to take a test.

Numbers
Operations
Factoring
Rational Numbers
Proportions and Ratios
Measurement Principles
Statistical Analysis
Displaying Information
Pre-Algebra Online Prep Course
If you want to be fully prepared, Mometrix offers an online Pre-Algebra prep course designed to give you everything you need to succeed!
Here’s what you’ll find in the Pre-Algebra course:
- 30+ Review Lessons Covering Every Topic
- Over 300 Pre-Algebra Practice Questions
- 30+ Video Tutorials
- Money-back Guarantee
- Mobile Access
Everyone learns differently, so we’ve tailored the Pre-Algebra online prep course to ensure every learner has what they need to prepare for the Pre-Algebra exam.
Click below to check it out!
Pre-Algebra Problems
LCM and GCF. What is the greatest common factor of 42 and 56?
The greatest common factor of two or more numbers is the largest integer that divides evenly into both numbers. It is helpful to list out the prime factors of each number and then collect all of the shared prime factors.
Start with 42. Since it is an even number, 2 must be one of its prime factors. After factoring out a 2, 21 remains. This can then be broken down into its prime factors, 3 and 7. So then \(42=2\times3\times7\).
| \(2\) | \(4\) | |
| \(3\) | \(21\) | |
| \(7\) |
\(42=2\times3\times7\)
Now, factor 56 using the same method.
| \(2\) | \(56\) | ||
| \(2\) | \(28\) | ||
| \(2\) | \(14\) | ||
| \(7\) |
\(56=2\times2\times2\times7\)
Now that both prime factorizations are complete, look at the factors for what is common between 42 and 56.
\(42=\mathbf{2}\times3\times\mathbf{7}\)
\(56=\mathbf{2}\times2\times2\times\mathbf{7}\)
Both share a 2 and a 7. Because of this, it can then be determined that the GCF of 42 and 56 must equal the product of these shared prime factors, \(2\times7\), which is 14.
Measurement Conversions. Stephanie is on a trip to Japan and is getting used to seeing speed limit signs posted in kilometers per hour (km/h) rather than miles per hour (mph). She sees a lot of signs that say “80 km/h” and wonders how fast that would be in miles per hour. Using the fact that 1 mile is approximately 1.6 kilometers, determine which of the following choices is equal to this speed in miles per hour.
To convert kilometers per hour to miles per hour, start by writing the known speed as a fraction over 1. In the numerator will be 80 kilometers, and 1 hour will be in the denominator since the speed is “per hour.”
\(\frac{80\text{ km}}{1\text{ hr}}\)
Now, write the conversion factor as a fraction. Since one mile is approximately 1.6 kilometers, this will be \(\frac{1\text{ mi}}{1.6\text{ km}}\). Multiply this with the known speed to cancel out unwanted kilometer units and adjust the number appropriately.
\(\frac{80\text{ km}}{1\text{ hr}}\times\frac{1\text{ mi}}{1.6\text{ km}}=\frac{80\text{ mi}}{1.6\text{ hr}}\)
Divide 80 by 1.6: \(80\div1.6=50\). Therefore, 80 km/h is equal to 50 mph.
Scientific Notation. Andre is researching the prevalence of various injuries in the United States and sees that there are 1.5 million cases of traumatic brain injury (TBI) annually among the population of 330 million Americans. Based on this, he calculates that approximately 0.004545 of the population sustains a TBI in a given year. How can he write this number using scientific notation?
Scientific notation is always written in the format \(m\times{10}^n\), where \(m\) is a rational number between 1 and 9, and \(n\) is an integer.
\(m\times{10}^n\)
\(1\le m\le9, n\in\mathbb{Z}\)
In order to change 0.004545 into a rational number between 1 and 9, the decimal must be moved into position right behind the first 4. Now the number is 4.545, which will be a part of the solution.
\(0004.\underparen {5}\underparen {4}\underparen {5.}\)
In order to equate this 4.545 to the true value of 0.004545, what must be done? The decimal point has to move back to the left three times. The action of moving the decimal to the left by one place is like dividing by 10. Therefore, moving the decimal to the left three times is like dividing by 10 three times. Equivalently, we say that 4.545 is being multiplied by \({10}^{-3}\). Because of this, \(0.004545=4.545\times{10}^{-3}\).
Mathematical Operations. Which of the four mathematical operations is associated with the terms “factor” and “product”?
In multiplication, the numbers being multiplied together are called the factors, while their result is the product. If you haven’t already, take a moment to commit these terms to memory, as they’ll come more into play down the road.
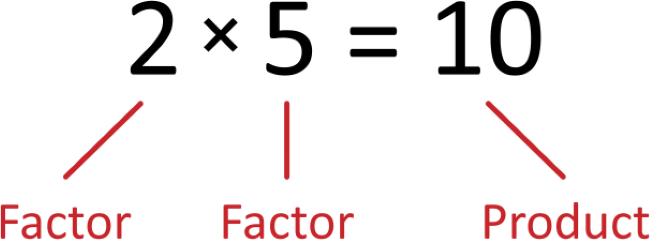
Commutative, Associative, and Distributive Properties. Which of the following statements demonstrates the commutative property?
The commutative property applies to addition and multiplication problems in such a way that appears sort of like a mirror. The numbers and operation on the left of the equals sign are reflected on the right side in a reverse order, as if an actual mirror is placed right in the middle.
Each of the following equations demonstrate the commutative property.
\(6\times2=2\times6\)
\(10+5=5+10\)
\(9\times20=20\times9\)
You can remember that this is the commutative property because the word “commutative” has two m’s in it, which stand for “mirror.” If there are more than 2 numbers on both sides, then the numbers can be arranged in any order and don’t have to be exactly mirrored.
The solution is not choice B or choice D because these are both examples of the associative property, which demonstrates that grouping numbers with parentheses does not affect the outcome of problems involving only addition or only multiplication.
The solution is not choice C because that is an example of the distributive property, where the 8 on the outside is multiplied with both the 2 and the 4 individually inside the parentheses.
Adding and Subtracting Fractions.Trevor and Max made two pizzas, that were the same size, for lunch. Trevor cut his pizza into 8 slices and ate 3 of them, while Max cut his pizza into 6 slices and ate 2 of them. How much pizza did they consume in total? Express your answer as a fraction of one whole pizza.
Since Trevor ate 3 slices from his pizza that was cut into 8 slices, it can be said that he consumed \(\frac{3}{8}\) of a pizza. Max, on the other hand, ate 2 slices from his pizza that was cut into 6 pieces. Therefore, Max ate \(\frac{2}{6}\), or \(\frac{1}{3}\), of a pizza. Together, they ate \(\frac{3}{8}+\frac{1}{3}\) of a pizza.
\(\frac{3}{8}+\frac{1}{3}\)
Do not cancel the diagonal 3’s; that can only be done in multiplication problems! Instead, these fractions must be combined using addition, which can be done after getting the fractions to have a common denominator.
The least common denominator is the least common multiple (LCM) of 8 and 3. Since 8 has a prime factorization of \(2×2×2\), and 3 is already prime, it can be noticed that these prime factorizations don’t have anything in common. Therefore, the LCM of 8 and 3 will equal \(2×2×2×3\), which is 24.
To rewrite each fraction to have a denominator of 24, multiply them by \(\frac{3}{3}\) and \(\frac{8}{8}\), respectively.
\((\frac{3}{3})\frac{3}{8}+\frac{1}{3}(\frac{8}{8})=\frac{9}{24}+\frac{8}{24}\)
Once both fractions share a common denominator, their numerators may be combined by adding. The denominator will stay as 24 because it doesn’t reflect the quantity of “pieces” but instead the size of each piece.
\(\frac{9+8}{24}=\frac{17}{24}\)
So, Trevor and Max ate a combined \(\frac{17}{24}\) of a pizza.
Converting Fractions into Decimals and Percentages. Amber conducted a survey for her statistics class and found that out of 20 people surveyed, 3 people were more than 6 feet tall. What percent of participants were taller than 6 feet?
The given information can be used to write the proportion of participants over 6 feet tall as a fraction. Since 3 out of 20 people met this qualification, it is true that \(\frac{3}{20}\) of participants were taller than 6 feet.
To write this as a percentage rather than as a fraction, set it up as a division problem.
| \(20\) | \(3\) |
Since 20 is larger than 3, write in the decimal point and tenths place, then proceed with the division.
| . | ||||
| \(20\) | \(\phantom{.}3\) | . | \(0\) |
| . | \(1\) | ||||
| \(20\) | \(\phantom{.}3\) | . | \(0\) | ||
| \(-\phantom{.}2\) | . | \(0\) | |||
| \(\phantom{.}1\) | . | \(0\) | |||
This division isn’t finished yet, so add the hundredths place and continue dividing.
| . | \(1\) | \(5\) | |||
| \(20\) | \(\phantom{.}3\) | . | \(0\) | \(0\) | |
| \(-\phantom{.}2\) | . | \(0\) | |||
| \(\phantom{.}1\) | . | \(0\) | \(0\) | ||
| \(-\phantom{.}1\) | . | \(0\) | \(0\) | ||
| \(0\) | |||||
Now the division is complete, and \(\frac{3}{20}\) is equal to 0.15. This decimal can be converted to a percentage by multiplying by 100%.
\(0.15=\left(0.15\times100\%\right)=15\%\)
Therefore, \(\frac{3}{20}=0.15=15\%\).
Computations with Percentages. Fill in the blank: 10 is 40% of _____.
To determine the solution to this problem, use the mathematical equivalents of the words “is” and “of.” For example, the word “is” represents that one thing is the same as something else; in other words, it represents equality. Replace the word “is” with an equal sign.
\(10\text{ is }40%\text{ of }\)_____
\(10=40%\text{ of }\)_____
Now, replace the word “of” with a multiplication symbol.
\(10=40%\times\) _____
To find the appropriate value for the blank, use a variable, like the letter \(n\), as a placeholder.
\(10=40%\times n\)
From here, convert 40% to a decimal place and solve for \(n\) by getting it by itself on one side of the equation.
\(10=0.40n\)
Divide both sides by 0.40.
\(\frac{10}{0.40}=\frac{0.40n}{0.40}\)
\(25=n\)
Since \(10\div0.40=25\), \(n\) must be 25. Therefore, 10 is 40% of 25.
Proportions. Sandra has a photograph that is 8 inches in length and 5 inches in width, and she wants to have the photo enlarged. In order to ensure that none of the image is lost along the sides, she needs the dimensions to remain proportional. If the enlarged photograph is to be 15 inches wide, what will its length be?

The dimensions of the initial photograph may be written as the ratio \(\frac{8}{5}\). Because the enlarged photograph will have a new width of 15 inches instead of 5, write a new ratio with 15 in the denominator. These two ratios will be equal because the photo enlargement will have the same proportions as the original.
\(\frac{8}{5}=\frac{?}{15}\)
To determine the missing value of the new length, notice that the width is increasing by a factor of three. To preserve the proportion of the dimensions, the length must also be multiplied by three.
\(8\times3=24\)
\(5\times3=15\)
\(\frac{8}{5}=\frac{24}{15}\)
Therefore, the length of the enlarged photograph is 24 inches.
Average. Determine the average of the following set of numbers: 12, 15, 19, 25, 31, 36.
The average is the weighted “center value” of a set of numbers, it can be found by adding up all the numbers and then dividing that sum by the number of values in the set. In this case, adding up all of the numbers in the set results in a sum of 138.
\(12+15+19+25+31+36=138\)
Because this set included 6 numbers, divide the sum, 138, by 6.
\(138\div6=23\)
Therefore, 23 is the average of this set of numbers.
