Ordering Rational Numbers

Hello, and welcome to this video on ordering rational numbers! This video will show you how to list rational numbers from least to greatest or greatest to least.

Rational Number Definition

First, let’s review the definition of a rational number. A rational number is any number that can be turned into a fraction with an integer in both the numerator and the denominator. \(\frac{1}{4}\) and \(\frac{9}{7}\) are examples of rational numbers. It’s also important to note that 0.25 and 25% are also rational numbers because they are equivalent to \(\frac{1}{4}\) and therefore can be turned into a fraction that divides two integers.

Ordering Rational Numbers

One of the easiest ways to order rational numbers is to turn them all into decimals and then put them in order. If we want to turn a percentage into a decimal, all we do is turn the percent sign into a decimal point and move it two places to the left. So 13% becomes 0.13, and 213% becomes 2.13. Turning fractions into decimals is a little bit more challenging but still doable. To turn a fraction into a decimal, we first have to remember that the fraction bar means divide. This means that \(\frac{3}{4}\) is really the same as \(3\div 4\). So if we want to turn \(\frac{3}{4}\) into a decimal, we simply use long division to divide \(3\div 4\).

4 can’t go into 3 at all, so we add a decimal point and put a 0. Since we added a decimal point here, we need to add it to the top as well. 4 goes into 30 seven times. \(7\times 4=28\), so we write 28 and subtract, and we’re left with 2. We then add another 0 and bring it down. And then see 4 goes into 20 five times. \(4\times 5=20\), and when we subtract we get 0.

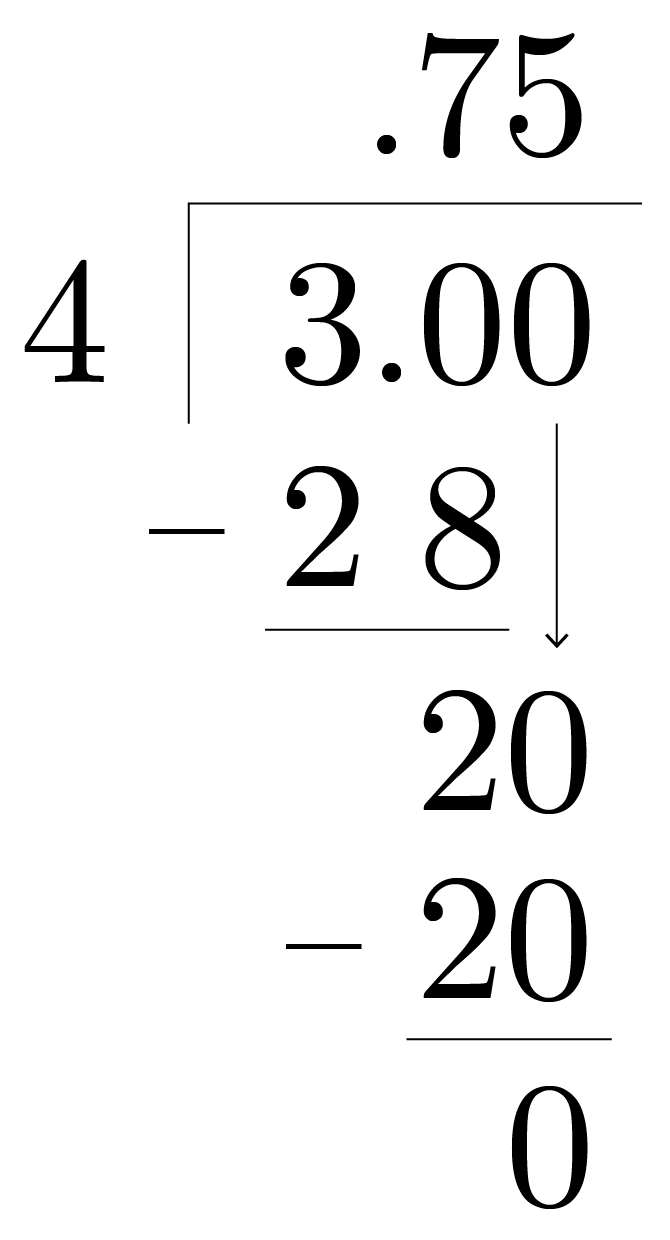
So \(\frac{3}{4}=0.75\).

Remember, some decimals continue for a really long time or end up repeating, so in these cases it might be helpful to round to three or four decimal places. That should give you enough information to know where to place that number in a list.

One other thing we need to look at is how to order square roots of numbers. You can turn them into decimals and order them that way, but that is usually pretty hard to do without a calculator. Another way is to recognize what two numbers the square root falls between. Let’s look at an example so I can show you what I’m talking about.

\(\sqrt{41}\)

 
41 is not a perfect square, so the way to estimate its square root is to find the two perfect squares on either side of it. The perfect square right below 41 is 36, and the one right above it is 49. Now, we know that the \(\sqrt{36}=6\) and the \(\sqrt{49}=7\). So the \(\sqrt{41}\) has to fall somewhere between 6 and 7.

Notice, this doesn’t give you a specific answer of what the\(\sqrt{41}\) is in decimal form, but it gives you a general location of where it would fall in a sequence of numbers, which is typically all that you need to put it in order.

Now that we have reviewed how to order numbers, let’s practice by putting this sequence of numbers in order from least to greatest:

\(87\%\), \(\frac{2}{9}\), \(\sqrt{78}\), \(\frac{45}{4}\), \(6.743\)

 
We are going to start by turning each of these into a decimal.

Remember, to turn a percent into a decimal, simply change the percent sign to a decimal point and move it two places to the left, so \(87\%=0.87\).

We can figure out what \(\frac{2}{9}\) is by dividing \(2\div 9\). Remember, a fraction bar always means divide!

So \(2\div 9\): 9 goes into 2 zero times. So we add a decimal and put a 0; putting a decimal up here also. 9 goes into 20 two times. \(9\times 2=18\), and then we subtract and get 2. If we add a 0 and bring it down we get 20. 9 goes into 20 two times; we get 18, subtract, and get 2.

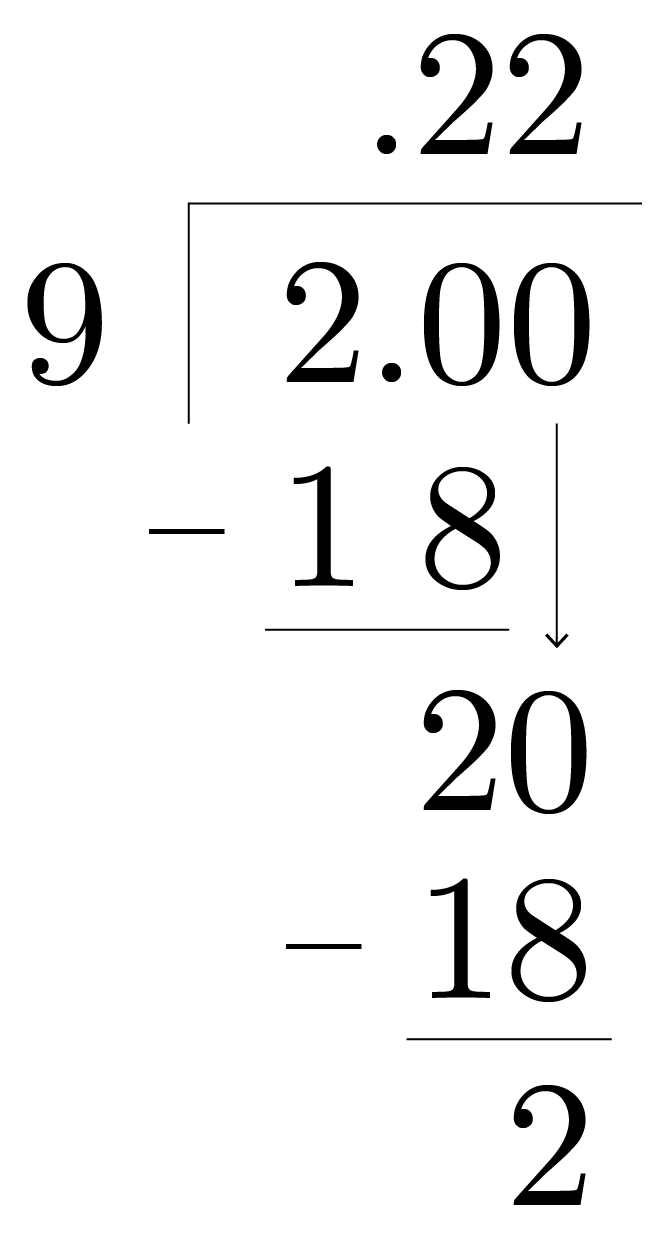
Notice that when we divide we get \(0.\bar{2}\), so for this exercise we will round to 0.222.

\(\frac{2}{9}\approx 0.222\)

When we look at a square root, remember we want to look for the two perfect squares that the number falls between. 78 falls between the perfect squares 64 and 81, which are the squares of 8 and 9 respectively. So the \(\sqrt{78}\) falls somewhere between 8 and 9.

\(8 < \sqrt{78} < 9\)

 
We can find \(\frac{45}{4}\) by dividing, just like we did with \(\frac{2}{9}\).

So \(\frac{45}{4}=11.25\).

And 6.743 is already in decimal format, so we don’t have to do anything with that number.

Now, all we have to do is put them in order from least to greatest. Before I do this, let me erase some of our scratch work so we have more room. When we do this, we get:

\(0.222\), \(0.87\), \(6.743\), \(\sqrt{78}\), \(11.25\)

 
Now, these aren’t our original values, so to get our final answer, we have to change our decimal values back into their originals.

\(\frac{2}{9}, 87\%, 6.743, \sqrt{78}, \frac{45}{4}\)

 
If you were asked to put these numbers in order from greatest to least, you would follow all the same steps except at the very end order them opposite to how we did it in this example, so \(\frac{45}{4}\) would be first and \(\frac{2}{9}\) would be last.

And that’s all there is to it! I hope this video on ordering rational numbers was helpful. Thanks for watching and happy studying!

Ordering Rational Numbers Practice Questions