Hi, welcome to this video on converting percentages to decimals and fractions! In this video, we’ll show you some easy and not-so-easy methods for converting percentages.
We use decimals in every part of our lives. You see decimals when dealing with money, measuring distance, measuring how much something weighs. There are decimals, literally, everywhere you look. But before we look at conversions, let’s do a quick recap on percentages.
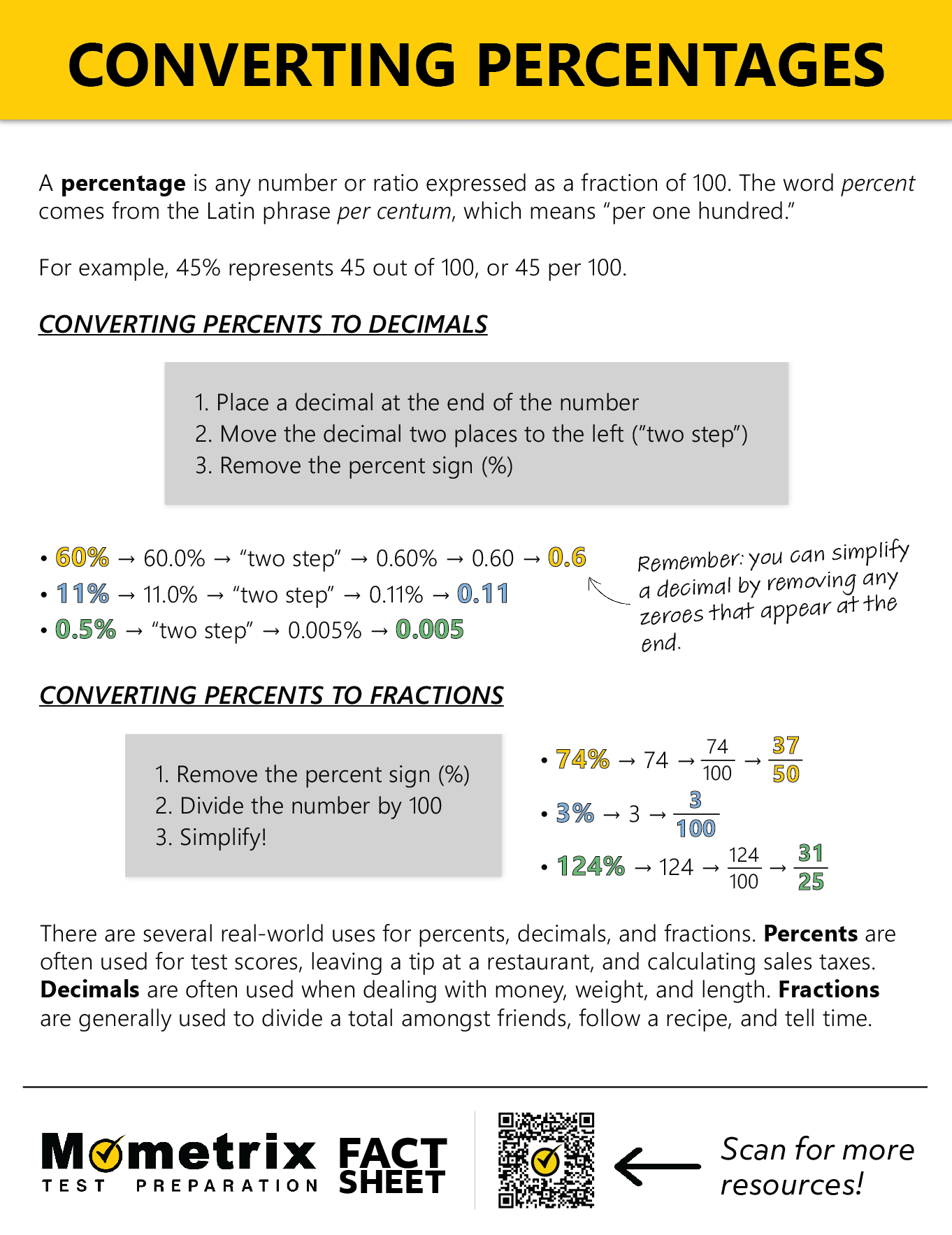
A percent is any number that is a part of 100. The word percent literally means “per one hundred.”
Percent to Decimal
For instance, 25% is 25 of 100, and 64% is 64 of 100. But how do you convert the percentage into a decimal? Well, there are actually two ways you can do it.
The first way is by using math.
We’ve already established that percent means “per one hundred.” Using 25, 25% is really just 25 per 100. If you divide 25 by 100, you get 0.25, which is a decimal.
But there’s a much easier way to convert to a decimal, and it’s something I like to call the math two-step. Just move the decimal in your percentage 2 places to the left.
Let’s use 25% as our example. 25 has two digits, the 2 and the 5.
Our decimal is after the 5. Moving the decimal two places to the left gives us 0.25. As always, remember to remove the percent sign when you’re done.
Simple, right? But what if your percent number is over 100%? Maybe you have 125%. Well, the same applies. Move the decimal point two places to the left. You would move past the 5 (the first point) and past the 2 (the second point) and end with 1.25.
Now that we’ve got that down, let’s look at converting percentages into fractions.
This conversion has a few more steps.
Percentage to Fraction
When you convert a percentage to a fraction, you first convert your percentage to a decimal, then divide that number by 1. Let’s stay with 25. 25% becomes 0.25. Now we divide that by 1.
Next, for every number after the decimal point, multiply by 10. Since there are two numbers after the decimal in our example, we multiply 10 twice. If there were four numbers after the decimal, we would multiply 10 four times. The multiplication factor is essential to remember. You’re not “adding” 10 after each decimal point. You’re multiplying. In this case, you’ll multiply 10 times 10, which equals 100. So you’ll multiply the top number and the bottom number by 100.
Now, you have to simplify the fraction. You do that by finding the highest number that divides the top and bottom number equally. In this case, the answer is 25.
25 is the highest number that equally divides both 25 and 100. Here’s how the equation looks.
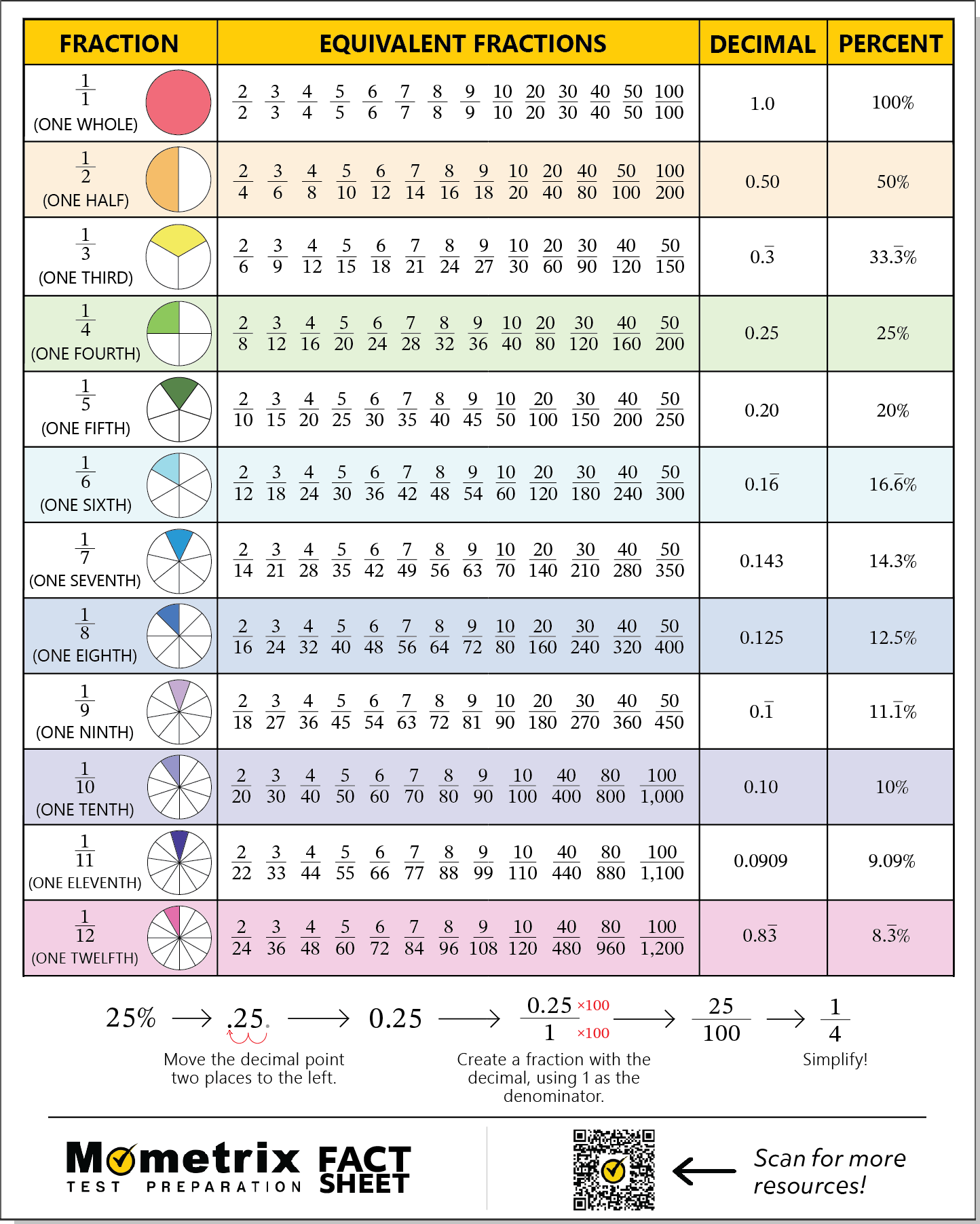
And there you have it! The answer is \(\frac{1}{4}\).
That’s our look at converting percentages to decimals and fractions, with a little simplification thrown in. By following this lesson, you should have a firm base for these calculations, which prove useful in many areas of our lives.
Thanks for watching and happy studying!
Frequently Asked Questions
Q
How do you change a percent to a fraction and decimal?
A
Change a percent into a fraction by taking the percent and placing it over 100. Then, simplify the fraction if needed.
Change a percent to a decimal by turning the percent sign into a decimal point and moving it two places to the left.
Ex. Change 16% into a fraction and a decimal.
Fraction: 16%=
Decimal: 16%→16.→0.16
Q
How do you convert percentages to decimals?
A
Convert a percentage to a decimal by turning the percent sign into a decimal point and moving it two places to the left.
Ex. Convert 49% to a decimal.
49%→49.→0.49
Q
How do I convert decimals to percentages?
A
Convert a decimal to a percentage by moving the decimal point two places to the right and then placing a percent sign at the end.
Ex. Convert 0.713 to a percentage.
0.713→71.3→71.3%
Q
How do you turn a normal number into a percentage?
A
Turn a normal number into a percentage by adding a decimal point followed by 2 zeroes. Remember, adding a decimal point and 0s to the end of a number does not change its value. Then, move the decimal point two places to the right, and add a percent sign. It’s the same process as converting a decimal to a percentage.
Ex. What is 14 as a percentage?
14→14.00→1400→1,400%
Q
How do I convert percentages to fractions?
A
Convert percentages to fractions by dropping the percent sign and placing the number over 100. Then, simplify if necessary.
Ex. Convert 45% to a fraction.
45%=
Converting Percentages to Decimals and Fractions PDF
Converting Percentage Practice Questions
What is 47% as a decimal?
The correct answer is 0.47. To convert a percent to a decimal, change the percent sign to a decimal point and move it two places to the left.
What is 29% as a fraction?
The correct answer is \(\frac{29}{100}\). Percent means “per 100,” so 29% means “29 per 100,” which looks like \(\frac{29}{100}\) as a fraction.
Which of the following is not a proper way to rewrite 40%?
The correct answer is 0.20. 40% as a decimal is 0.40. As a fraction it is \(\frac{40}{100}\), which can be simplified to \(\frac{2}{5}\) by dividing both the numerator and denominator by 20. 0.20 as a percent is 20%.
What is 486% as a decimal?
The correct answer is 4.86. To convert a percentage to a decimal, change the percent sign to a decimal point and move it two places to the left.
What is 38% as a fraction?
The correct answer is \(\frac{19}{50}\). To convert a percentage to a fraction, place the number before the percent sign as the numerator of a fraction over 100: \(\frac{38}{100}\). Then, simplify by dividing both the numerator and denominator by 2: \(\frac{19}{50}\).