
Hi, and welcome to this review of decimals! Before we dive in, we will need to have a solid understanding of place value.
Place Value
Decimals and place value go hand in hand, so it can be tough to make sense of one without having some background experience with the other. Take a look at this place value chart.
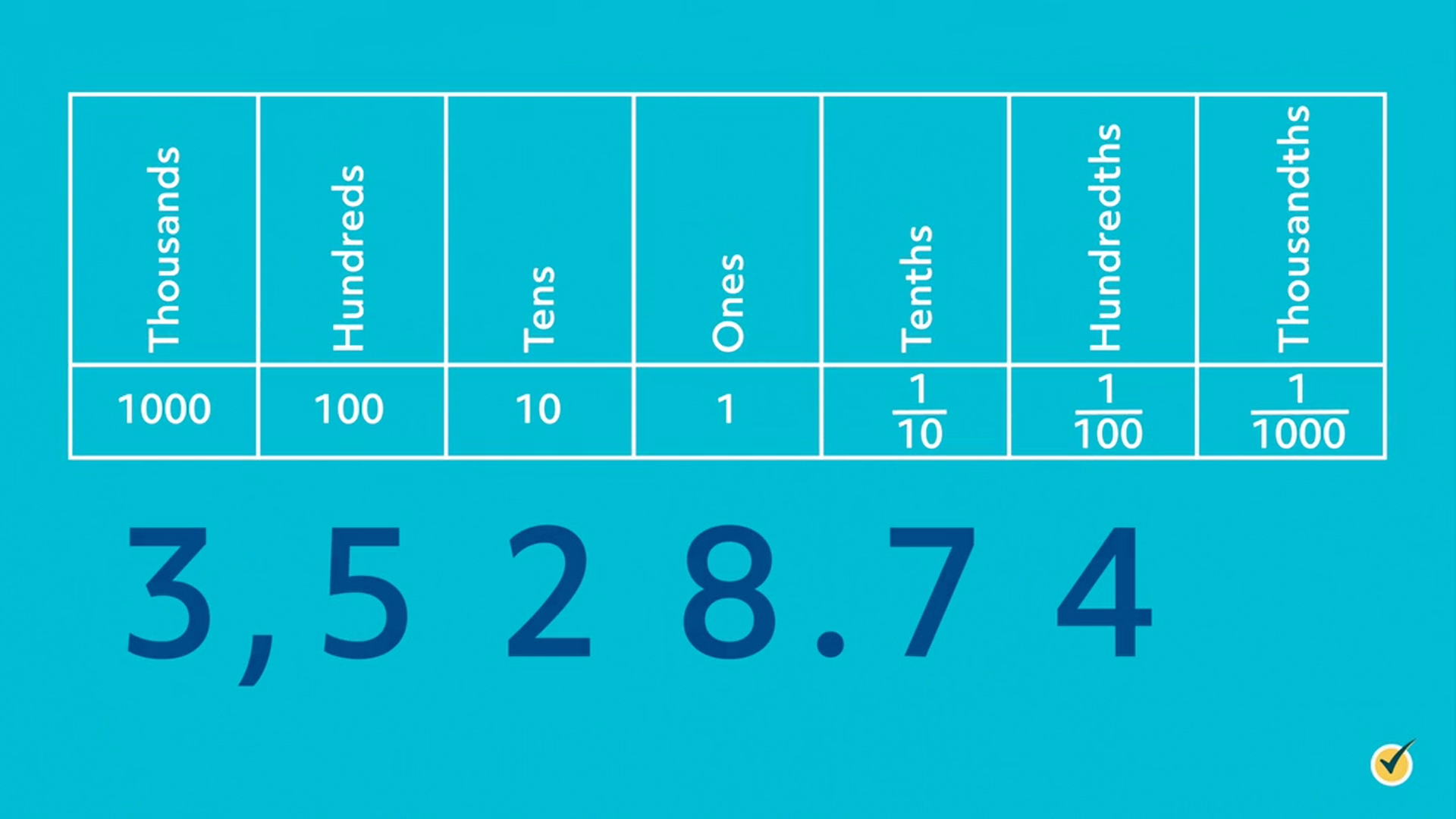
With this example of 3,528.74, we can see that each movement to the right of the decimal point drops us down by a factor of 10. We move from tenths, to hundredths, to thousandths. On the other hand, as we move to the left of the decimal point, we increase by a factor of 10 each time. We move from tens to hundreds to thousands. This base 10 number system is not the only number system in use today, but it is very common and widely used around the world.
Let’s look at another example. This time, let’s use the number 136.289. This number as a value is read as “one hundred thirty-six, and two hundred eighty-nine thousandths.” Let’s break this value up into its different parts in the terms of place value. In this example, we look at each digit and then take note of where it is in relation to the decimal point to determine the total value of the number.
The digit 2 is located in the tenths position, so it does not represent the value “2” but “2 tenths.” The digit 1 is located in the hundreds position, so it does not represent a value of “1” but a value of “1 hundred.” When you break apart a decimal value into its different parts, you are essentially thinking about the number in its expanded form. You are looking at each digit, and identifying how much this digit represents based on its location. The location of each digit reveals its value, or “place value.” This is similar to the process of writing a number in expanded form.
Our number 136.289 would be \(100 + 30 + 6 + 0.2 + 0.08 + 0.009\), in expanded form. This can sometimes be helpful in order to see each digit as an independent value.
The place value as a system allows us to write and express numbers with extreme accuracy. For example, instead of simply rounding the amount of fuel needed for an important mission to the moon as approximately 950 gallons, we could instead say with complete accuracy and confidence that the amount needed for a safe trip would be exactly 950.458 gallons.
Another helpful way to visualize place value is by using money. We know that one dollar can be represented by 10 dimes. We also know that one dollar can be represented by 100 pennies.
This is similar to saying that one whole can be represented by 10 tenths or by 100 hundredths.
$1 = 10 dimes
One dime is one tenth of a dollar (\(\frac{1}{10}\))$1 = 100 pennies
One penny is one hundredth of a dollar (\(\frac{1}{100}\))
With this understanding of place value, we are ready to dive into the topic of decimals.
Decimals
Operations with decimals is a topic that most of us use in our daily lives, especially when dealing with money.
For example, 5 dollars, 2 dimes, and 5 pennies is represented by the decimal number $5.25. If we remember our place values, the 5 in the ones place represents 5 dollars, the 2 in the tenths position represents 20 cents (or 2 tenths), and the 5 in the hundredths position represents 5 cents (or 5 hundredths).
In the real world, it is often convenient to work with fractions and mixed numbers. Other times, it makes more sense to work with decimals. If we want to talk about measuring amounts in a recipe, it is generally helpful to use fractions. On the other hand, when we are dealing with something like temperatures, it is often more efficient to use decimals.
Using fractions, mixed numbers, or decimals does not change the amount, it simply changes the form. For example, if a recipe calls for 4/5 cups of flour, this is the same amount as the decimal 0.8. These values are equivalent.
All decimal values can be written as fractions, mixed numbers included. For example, when writing the decimal value 5.25 as a mixed number, we simply need to look at each digit and then note its location.
With the value 5.25, we would represent the first 5 in the ones position as simply 5. Then, we look at the values to the right of the decimal. We see .25. This reaches out to the hundredths place, so it is representing twenty-five hundredths, or as a fraction \(\frac{25}{100}\). So, 5.25 as a mixed number would be \(5\frac{25}{100}\). We can simplify the fraction, making it \(5\frac{1}{4}\).
As you can see, using decimals is something we do on a regular basis, and being able to convert between decimals and fractions can ensure that our number is as accurate as possible.
I hope this review was helpful! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What is a decimal?
A
A decimal number is any number that uses a decimal point to show the part of the number that is less than one.
Ex. 16.275
Q
How do you round decimals?
A
Round decimals the same way you round non-decimal numbers. Check the number in the place value one below the one you are rounding to. If it is greater than or equal to 5, round up. If it is less than 5, round down. Then, only write the numbers until you reach the place you are rounding to.
Ex. Round 8.715 to the nearest whole number.
Since 7 is greater than 5, round up. 8.715 rounds to 9.
Ex. Round 63.271 to the nearest hundredth.
Since 1 is less than 5, round down. 63.271 rounds to 63.27.
Q
Can an integer be a decimal?
A
By the definition of an integer, no, an integer cannot have a fractional part. However, an integer can be turned into a decimal by adding a decimal point and zeroes after the number.
Q
What is a repeating decimal?
A
A repeating decimal is a decimal that has a number that repeats forever. It is usually represented by placing a bar over the repeated number.
Ex. \(0.\overline{3}=0.33333…\)or \(0.\overline{16}=0.1616… \)
Q
Are decimals rational numbers?
A
Yes, most decimal numbers are rational numbers. A rational number is any number that can be turned into a fraction, so any decimal number that ends or repeats. One notable decimal number that is not rational is pi (3.14…) because it is a decimal that never ends or repeats.
Decimal Practice Questions
Which shows the number “three hundred forty three, and twenty five hundredths”?
The correct answer is C: 343.25.
The first part of the statement “three hundred forty three” is describing the part of the number before the decimal. The word “and” indicates the decimal and the word “hundredths” informs us the number has two digits after the decimal.
Which shows the number 429.317 in expanded form?
The correct answer is D: \(400+20+9\)\(+0.3+0.01+0.007\).
With the place value chart in mind, for the number 429.317, the 4 is in the hundreds place, the 2 in the tens place, the 9 in the ones place, the 3 in the tenths place, 1 in the hundredths place, and 7 in the thousandths place.
What is 836.1792 rounded to the nearest hundredth?
The correct answer is C: 836.18.
The hundredths place is two digits after the decimal. The same rule for rounding whole numbers is used when rounding a decimal; therefore, since the number in the thousandths place is 9, the 7 is rounded up to 8.
What is \(3\frac{6}{100}\) in decimal form?
The correct answer is C: 3.06.
When converting a mixed number to a decimal, the 3 in the ones place is converted to 3 and the fraction \(\frac{6}{100}\), or six hundredths, is converted to 0.06 when you divide the numerator by the denominator.
What is 2.75 in fraction form?
The correct answer is A: \(2\frac{3}{4}\).
When converting a decimal to a fraction, the 2 in the ones place remains as a 2. Since the .75 is to the hundredths place, we can convert it to \(\frac{75}{100}\), so the mixed number is \(2\frac{75}{100}\), or \(2\frac{3}{4}\) when the fraction is simplified.
