
Although it may be easier to deal only with whole numbers, such as 2, 45, or 120, if you look carefully, decimals appear frequently throughout our daily lives.
For example, an item at a store could cost $2.75, or your favorite basketball player may average 19.7 points per game. You could take out a loan with a 4.45% interest rate, or the winner of the 100-meter relay may have completed the race in 12.67 seconds.
In order to use decimals effectively, it is important to be able to utilize and manipulate decimals in mathematical expressions.
Today, we’re going to cover the basics—addition and subtraction.
Adding Decimals
We’ll start with a simple example of adding decimals, so let’s try it:
The first step, like you can see, is to line up the two decimals like so:
| \(32.61\) | |
| \(+\) | \(11.54\) |
Note that because of the commutative property of addition, it does not matter which decimal is placed first (however it will make a difference when we do subtraction).
Make sure that the decimal points in each number are lined up exactly. If your decimals are not lined up correctly, you will end up with the wrong answer.
Once you have your two decimals lined up, you begin to solve the problem as you would with any addition problem.
First, we add the two numbers in the hundredths place, \(1\) and \(4\), which gives us \(5\) in the hundredths place. We then add \(6\) and \(5\), which are in the tenths’ place, and that gives us 11, so we carry the 1. Bring down our decimal, and now we have \(2+1+\) this other \(1\), so it’s \(3\), \(4\). And now we add \(3\) and \(1\) and get \(4\). So our final answer is \(44.15\).
| \(32.61\) | |
| \(+\) | \(11.54\) |
| \(44.15\) |
Subtracting Decimals
Let’s move over to subtraction. We’ll start with a simple problem:
Just as with addition, the first step is to line up the numbers with the decimal point in the same place. Your expression should look like this:
| \(7.5\) | |
| \(–\) | \(2.8\) |
Begin to subtract as you would any subtraction problem. Starting in the tenths’ column, you will need first to borrow from our ones’ column because \(5-8\) doesn’t work out. So, take \(1\), make this \(6\), and then carry it over. So now we have \(8\) being subtracted from \(15\), which gives us \(7\). Bring down our decimal, and now we have \(2\) being subtracted from \(6\), which gives us \(4\). So our final answer is \(4.7\).
| \(7.5\) | |
| \(–\) | \(2.8\) |
| \(4.7\) |
Finally, let’s do one more subtraction problem:
Once again, we line up our two numbers, making certain that our decimal points are in the same position. Your expression should look like this:
| \(10.53 \phantom{0}\) | |
| \(–\) | \(4.274\) |
You may want to add zeros to balance out, so it looks, just feels like it’s full there, which is fine. You can not add them, and that’s fine too.
| \(10.530\) | |
| \(–\) | \(4.274\) |
Once again, in this problem, we need to begin by borrowing from our hundredths place. So we make this a \(2\) and bring our \(1\) over so now we have \(4\) being subtracted from \(10\), which gives us \(6\). Then we have \(7\) being subtracted from \(2\) which doesn’t work, so we need to borrow again. This becomes \(4\), carry over a \(1\) to have \(12\) so \(7\) being subtracted from \(12\), that gives us \(5\). Now we have \(2\) being subtracted from \(4\) which gives us \(2\). Bring down our decimal point, we have \(4\) being subtracted from \(0\), which we know does not work, so this becomes \(0\). Carry our \(1\) and we have \(10-4\) which gives us \(6\). So our final answer is \(6.256\).
| \(10.530\) | |
| \(–\) | \(4.274\) |
| \(6.256\) |
You should now have a strong understanding as to how to add and subtract decimals. Remember to always line up your numbers and make sure the decimals of each number are in the same place!
Thanks for watching, and see you guys next time!
Frequently Asked Questions
Q
What are the steps for adding and subtracting decimals?
A
To add or subtract decimal numbers, set up the numbers as usual for vertical addition or subtraction, aligning the numbers at the decimal points. Add extra zeroes after the decimal if necessary. Add or subtract as normal, keeping the decimal in the same position.
Ex. 243.5 + 1.279 =

243.5 + 1.279 = 244.779
Q
How is estimation helpful when adding and subtracting decimals?
A
Estimation is helpful when adding and subtracting decimals because it helps you know if your answer is close to the right answer or not.
For example, say you added 12.4 + 2.73 and got 3.97. Rounding each number to the nearest whole number would give you 12 + 3, which equals 15. 3.97 isn’t anywhere close to that, so you know you must have made an error somewhere. You go back to your original work and notice that you forgot to align your decimal points. Now you can fix your problem and get the correct answer of 15.13.
Q
Why is it important to line up decimals when adding?
A
It is important to line up decimals when adding because it ensures you are adding the correct place values.
Q
How do you subtract decimals from whole numbers?
A
Subtract decimal numbers from whole numbers by turning the whole number into a decimal by adding a decimal point and as many zeroes as needed. Then, subtract as normal.
Ex. 12 – 8.13
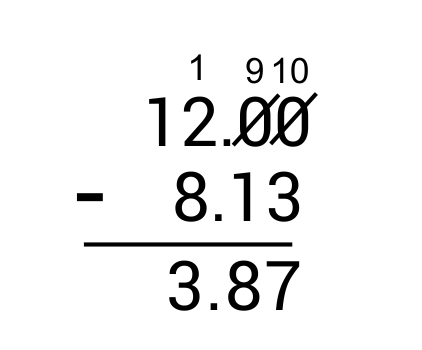
Q
How do you subtract negative decimals?
A
Subtracting a negative number is like adding that number. So, subtracting a negative decimal is adding that negative decimal.
Ex. -2.3 – (-7.4) = -2.3 + 7.4 = 5.1
Q
How do you subtract repeating decimals?
A
Subtract repeating decimals by turning them into fractions and subtracting the fractions, or by rounding the repeating decimals and subtracting.
Ex. \(0.\overline{6}-0.\overline{3}\)
\(0.\overline{6}=\frac{2}{3}\) and \(0.\overline{3}=\frac{1}{3}\)
\(\frac{2}{3}-\frac{1}{3}=\frac{1}{3}\)
OR
\(0.\overline{6}≈0.67\) and \(0.\overline{3}≈0.33\)
\(0.67-0.33=0.34\)
Adding and Subtracting Decimals Practice Questions
\(4+17.31=\)
The correct answer is 21.31. To add decimals, line up the decimal points on top of one another, add zeroes where necessary as placeholders, and add as normal. Remember, if there is no decimal point, it is at the end of the number.
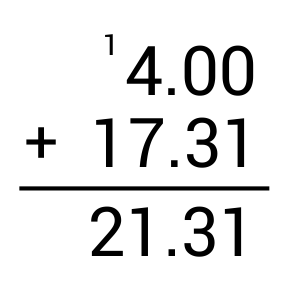
\(16.17+2.421=\)
The correct answer is 18.591. To add decimals, line up the decimal points on top of one another, add 0s where necessary as place holders, and add as normal.
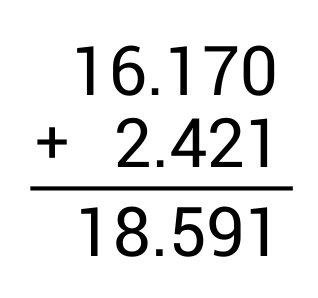
\(78.179-1.23=\)
The correct answer is 76.949. To subtract decimals, line up the decimal points on top of one another, add 0s where necessary as place holders, and subtract as normal.
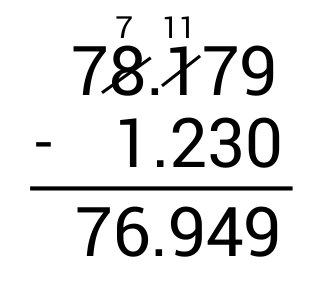
Susie is baking cinnamon rolls and needs 0.63 tsp of cinnamon for the dough, 3.71 tsp of cinnamon for the filling, and 0.12 tsp of cinnamon for the icing. How many teaspoons of cinnamon does she need total?
The correct answer is 4.46 tsp. When solving word problems, look for clue words that help you know what the question is asking. The main clue word in this problem is “total,” which tells us we need to add our values together.
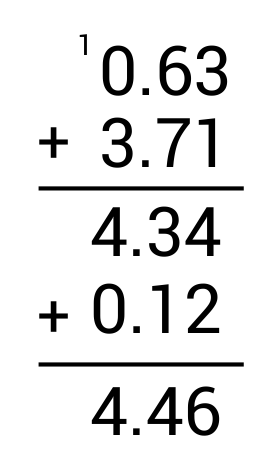
Jonathan gets $45 for his birthday. He spends $29.73 on a video game, $1.12 on a package of gum, and $2.81 on a soda. How much money does he have left?
The correct answer is $11.34. When a word problem asks how much is left, it often involves subtraction. Jonathan starts with $45 and then uses that money for three different things. Subtract the price of each item from his starting value to determine how much money he has left. First, subtract $29.73 for the video game.
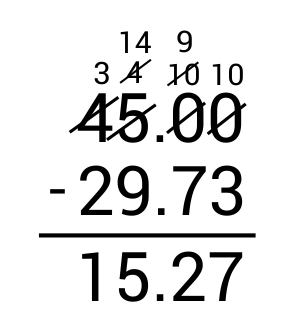
Then, subtract $1.12 for the package of gum.
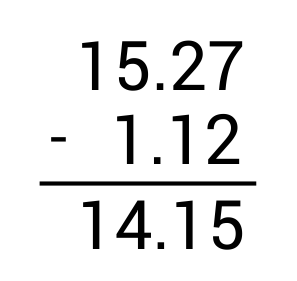
Finally, subtract $2.81 for the soda.
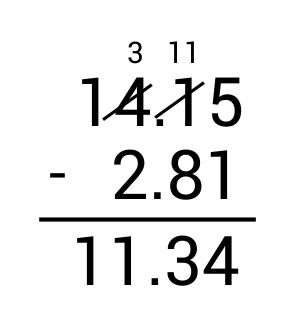
Jonathan has $11.34 left.
Zola buys 22.31 ounces of hard candy and 16.58 ounces of gummy candy. What is the total amount of candy that Zola buys?
The correct answer is B: 38.89 ounces.
When adding two numbers with decimal places, we line up the numbers and add the numbers in the hundredths place together \((8 +1)\) and the tenths place together \((3+5)\), and the ones place together \((2+6)\), and the tens place together \((2+1)\).
Cannon buys 16.56 pounds of pears and 13.42 pounds of grapes. How many pounds of fruit did Cannon buy?
The correct answer is B: 29.98 pounds.
When adding numbers with decimal places, we line up the numbers and add the numbers in the hundredths place together \((6+2)\) and the tenths place together \((5+4)\), and the ones place together \((6+3)\), and the tens place together \((1+1)\).
