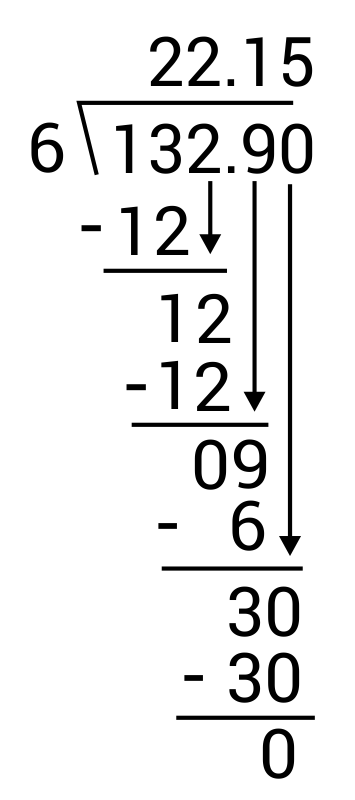Hey, guys! Welcome to this video on dividing decimals! Dividing decimals may not seem like the most useful tool, but it can actually come in handy for several situations in everyday life.
Now, you may be wondering when dividing decimals would ever be useful. Well, let’s say you had $26.84 in your bank account and you wanted to buy gas for your car without going over your budget. Each gallon costs $3.69 and you’d like to tell the attendant how many gallons to put in your car. How many gallons of gas should you ask for?
Or let’s say you are constructing a house, and need pieces of wood that are 4.85 feet long. The local store sells large beams of wood that are 28 feet long. At the store, you wonder: how many pieces of wood can you cut out of each beam?
Having the ability to divide numbers with decimals would help you in these situations.
Dividing Decimals
Let’s start with a basic example. Say you wanted to divide 4.5 by .5.
Your first step would be to write out the problem as you would any other long division problem. It should look like this:
When solving this problem, it would be significantly easier to work with whole numbers instead of numbers with decimals.
The simplest way to accomplish this is by multiplying each number in the expression by 10. As a general rule, every time you multiply a number by 10, you are essentially moving the decimal point over one place to the right. If we multiply .5 and 4.5 by 10, we get:
Now, you would solve \(45\div 5\) as you normally would. Since this is a relatively straightforward problem, we don’t need to go through the steps of long division. \(5\times 9=45\).
You may be wondering if we need to do something to modify this answer. After all, we did change both numbers in our expression. How can the answer be correct for our original expression? However, if you pull out your calculator, you will see that dividing 4.5 by .5, our original expression, also yields 9, just like dividing 45 by 5.
Dividing Decimals by Decimals
Let’s try a more complicated example: we’ll divide \(15.75\div 3.5\).
The first step is to multiply each number by 10 in order to turn these numbers with decimals into whole numbers. Starting with 3.5, that would give us 35. However, if we look at the other number in our expression, 15.75, we notice that multiplying it by 10 once does not suffice. That would give us 157.5, which is still not a whole number. So then what do we do in this instance?
Remember a key rule in dividing numbers with decimals—you need to do the same thing to both numbers in the expression. To make 15.75 a whole number, we need to multiply it by 10 twice, or, you could say, we need to multiply it by 100. That in effect moves the decimal place over two places to the right, giving us 1,575.
As we mentioned, we need to do the same thing to both numbers, so now we multiply 3.5 by 10 twice (or by 100). We move the decimal over two places to the right, and add a zero to fill the empty place. So now we have \(1,575\div 350\).
The problem is now long division. 350 does not go into 1, 15, or 157, so we need to guess how many times it goes into 1,575. 350 goes into 1,000 around 3 times, so 4 would be a good estimate for the number of times it goes into 1,575. Let’s do some quick multiplication to double-check. \(350\times 4\).
So when we multiply, \(4\times 0=0\), and we multiply \(4\times 5\) to get \(20\). Carry the \(2\), \(4\times 3=12\), then we add the \(2\), which gives us \(14\). So then we have \(1,400\), which is the best fit we’re going to get into \(1,575\). So now we write \(4\) above our \(5\), so now we have \(1,575-1,400\), which leaves us with \(175\) left over.
So now we want to be sure to add a decimal after the 4 on the top as well.
Now we divide \(1,750\div 350\) with some trial and error. Given that we saw before that \(350\times 4=1,400\), we can see that \(350\times 5\) is going to give us exactly \(1,750\), which means that we add a \(5\) right after the decimal place right next to our \(4\). This gives us a final answer of \(4.5\).
While dividing decimals may have seemed daunting at first, remember that it is essentially the same as regular long division. Don’t forget the strategy we discussed in order to turn our numbers with decimals into whole numbers: multiply both numbers in the expression by a multiple of 10 to move the decimal point over as many times as necessary. Treat both numbers the exact same way and you’ll be sure to end up with the correct answer.
I hope that this video was helpful! See you guys next time!
Frequently Asked Questions
Q
How do you divide decimals?
A
Divide decimals by multiplying both numbers by a factor of 10 so the divisor no longer has a decimal value. Then, use long division to divide as normal. Place the decimal point in the quotient directly above the decimal point in the dividend.
Here’s an example: \(7.205 ÷ 0.05 =\)______
Multiply both by 100 to get rid of the decimal part in the divisor.
\(720.5 ÷ 5\)
Then, use long division to divide.
Q
How do you divide decimals by whole numbers?
A
Divide decimals by whole numbers the same way you divide whole numbers by each other, but put the decimal point in the answer at the same place it is at in the original number.
Here’s an example: \(8.342 ÷ 2=\) ________

Q
How do you divide decimals without a calculator?
A
Divide decimals using long division, being sure to multiply by a product of 10 if there is a decimal in the divisor. Place the decimal point in the quotient directly above where it is in the dividend.
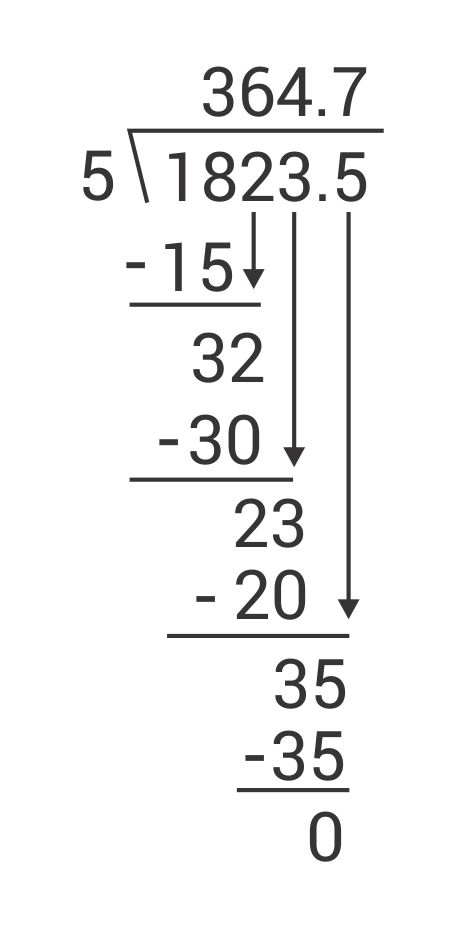
Here’s an example: \(182.35 ÷ 0.5\)
First, multiply both numbers by 10 so there is no longer a decimal in the divisor (0.5).
\(1,823.5 ÷ 5\)Then, use long division to divide.
Q
How do you divide decimals using models?
A
To divide decimals using models, first shade in the first number, your dividend. Then, circle groups of the second number, your divisor. The number of circled groups is your answer, or quotient.
Here’s an example: \(2.5 ÷ 0.5\)
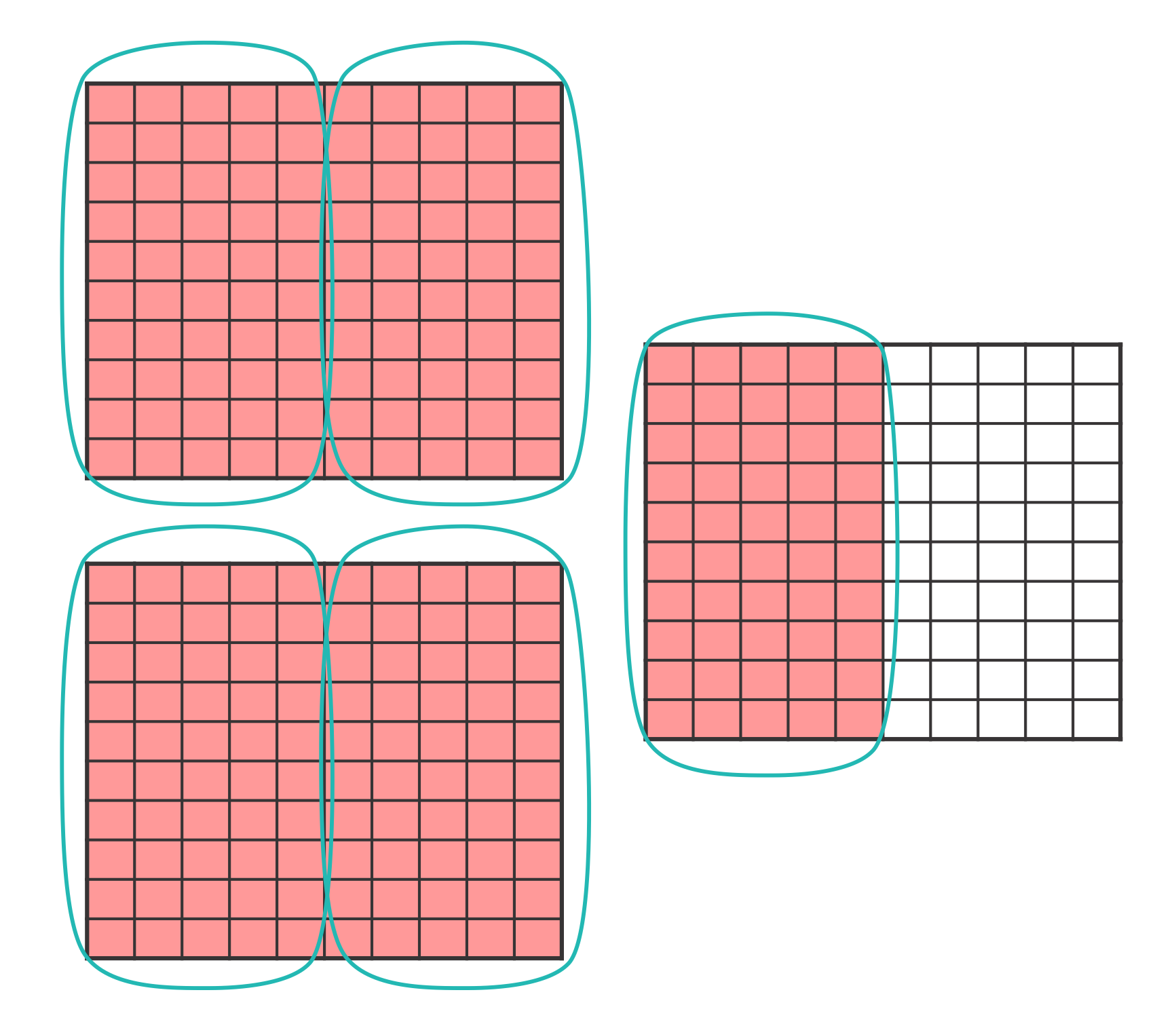
There are 5 groups so \(2.5 ÷ 0.5 = 5\).
Q
What do you do with a remainder when dividing decimals?
A
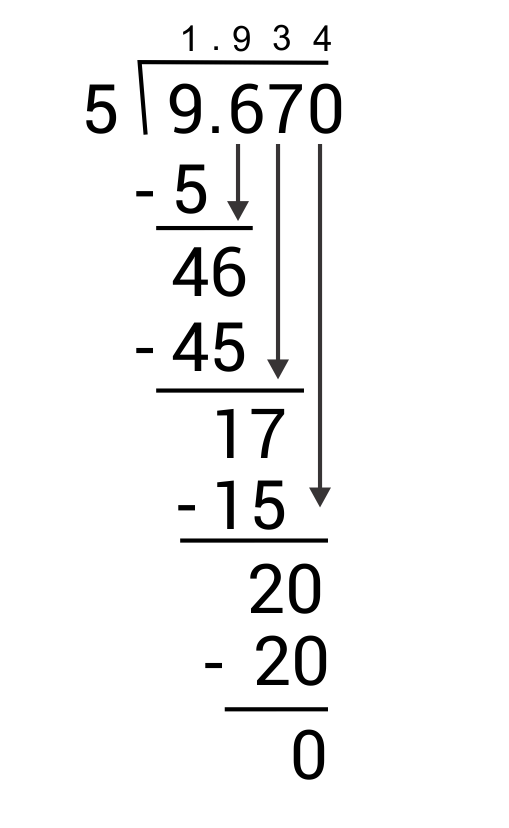
If there is a remainder when dividing decimals, add zeroes to the end of the dividend and keep dividing until there is no remainder.
Here’s an example: \(9.67 ÷ 5\)
Dividing Decimals PDF
Improve your math skills with our comprehensive fact sheet on how to divide decimals.
Dividing Decimals Problems
What is \(23.95÷5\)?
The correct answer is 4.79. To divide a decimal number by a whole number, long divide as you would with two whole numbers, but put the decimal point in the answer at the same place it is at in the dividend.
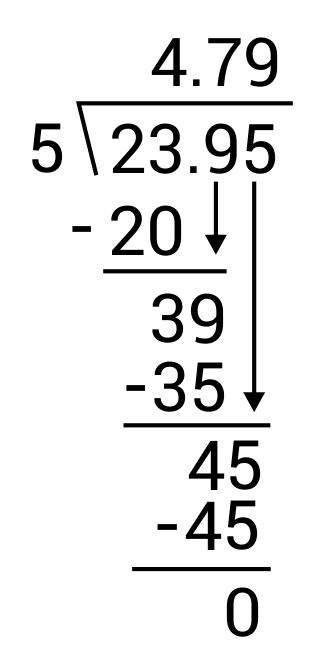
What is \(1.437÷2\)?
The correct answer is 0.7185. To divide a decimal number by a whole number, long divide as you would with two whole numbers, but put the decimal point in the answer at the same place it is at in the dividend. If it does not divide evenly, add a 0 to the end of the dividend and continue dividing until there is no remainder.
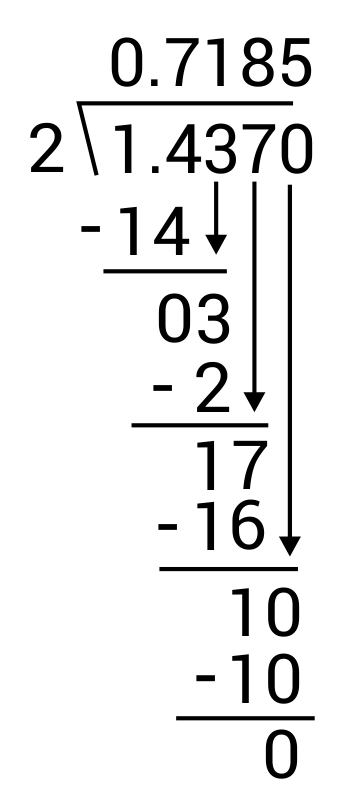
What is \(69.27÷0.3\)?
The correct answer is 230.9. First, multiply both numbers by 10 to get rid of the decimal part in the divisor.
\(692.7÷3\)
Then, use long division to divide.
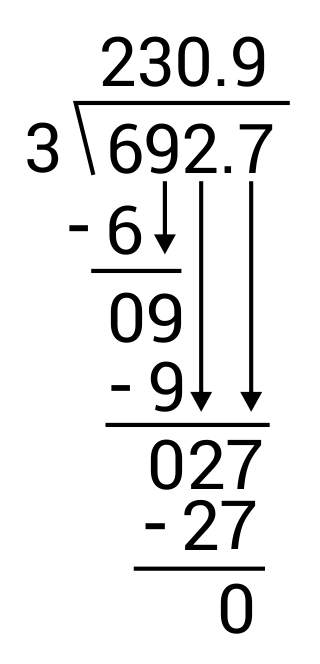
What is \(18.69÷0.005\)?
The correct answer is 3,738. First, multiply both numbers by 1,000 to get rid of the decimal part in the divisor.
\(18,690÷5\)
Then, use long division to divide.
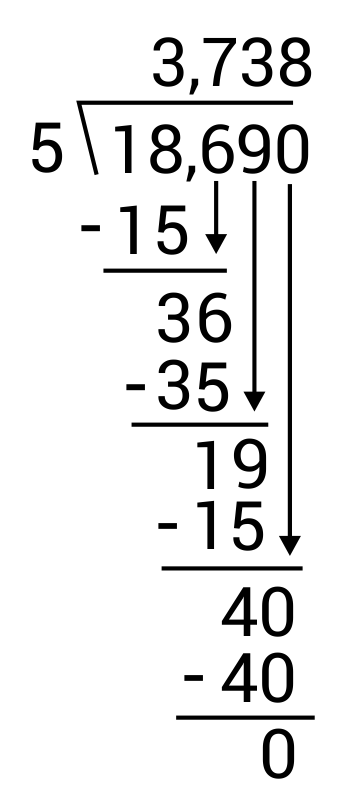
What is \(1.329÷0.06\)?
The correct answer is 22.15. First, multiply both numbers by 100 to get rid of the decimal part in the divisor.
\(132.9÷6\)
Then, use long division to divide.