
Hey guys! Today, we are going to take a look at the mathematical operations: addition, subtraction, multiplication, and division. These four operations serve as the fundamental building blocks for all math, so it is crucial to have a solid understanding to build upon. Let’s dive in.
Addition and Subtraction
We use addition and subtraction to solve many real-world situations. Addition and subtraction are simply the mathematical terms used to describe “combining” and “taking away.” When we add, we are combining, or increasing. When we subtract, we are taking away, or decreasing.
As a reminder:
- The symbol we use for addition is \(+\)
- The answer to an addition problem is called the sum
- The symbol we use for subtraction is \(–\)
- The answer to a subtraction problem is called the difference
Essentially, addition and subtraction are opposite operations. One adds value, and the other deducts value. One strategy for visualizing these two operations is to use a number line. We will use a number line to illustrate the following examples.
Let’s imagine a situation that involves the sale of popcorn. For this scenario, let’s assume that you are trying to raise money by selling bags of popcorn, and you start with 20 bags.
When your first customer arrives, they wish to purchase 4 bags of popcorn. This means that your remaining number of bags will decrease. We can represent this situation with a simple equation that involves subtraction. We started with 20 bags, and we “decreased by 4,” or subtracted 4. Our subtraction equation is written as \(20-4=16\).
On a number line, we can represent this deduction by starting at 20 and then moving backward four units in the negative direction. Each jump backward represents subtraction by 1.
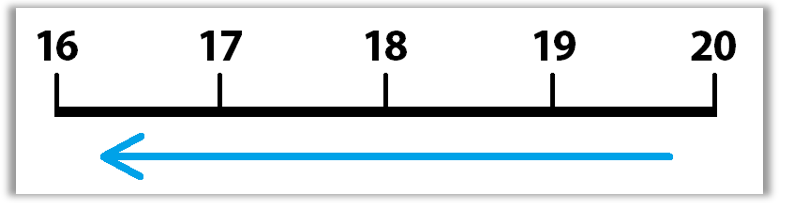
Now, let’s say you started with 20 bags of popcorn and ended up with 6 bags left at the end of the day. You need to replenish your stock in order to keep up your sales, so you make 4 more bags of popcorn. How many bags of popcorn do you now have available to sell? For this scenario, since we are looking at an increase of bags, we will use addition.
This situation can be described using the equation \(6+4=10\). You had 6 bags initially, and then “combined” that amount with 4 more bags. Now you have 10 bags in all. On a number line, addition is represented by jumps to the right, in the positive direction. Each jump to the right represents the addition of one unit. So in this example we would be starting at 6, and jumping 4 units to the right. We can see that we land on 10.
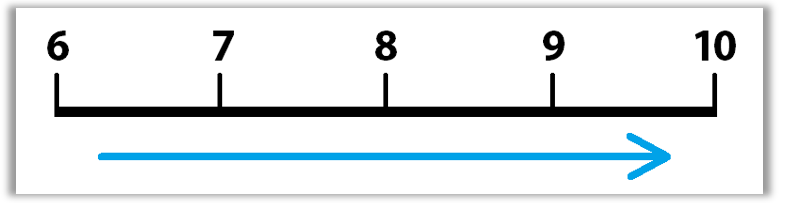
It is important to notice that when using addition, the order of the values does not matter. For example, \(10+30\) is the same as \(30+10\). The placement, or arrangement of the values has no effect on the outcome. Both arrangements would equal 40. However, the same is not true for subtraction. Does \(30-10\) mean the same thing as \(10-30\)? Clearly not. We can see that the order matters when dealing with a situation involving subtraction. The technical term for this quality is known as the commutative property. Essentially, this property is true for operations where the values can move around, “commute”, and the outcome of the expression or equation will not change. The commutative property applies to addition, but not to subtraction.
Multiplication and Division
Another operation that also shares the commutative property is multiplication. Let’s discuss multiplication together with division, as we did for addition and subtraction. Multiplication and division are similar to addition and subtraction in that they perform opposite functions. The function of multiplication is to represent multiple groups of a certain value, whereas division is designed to show the separating or subdividing of a value into smaller groups.
As a reminder:
- The symbol we use for multiplication is \(\times\)
- The answer to a multiplication problem is called the product
- The symbol we use for division is \(\div\)
- The answer to a division problem is called the quotient
Multiplication is essentially a convenient and time-efficient way to show what’s called “repeated addition.” For example, if you need to fill 30 bags of popcorn, and each bag requires 60 kernels, it could take hours to count up how many kernels you need in total by just using addition. A faster and more efficient way to make this calculation would be to use repeated addition. Instead of counting each seed independently, we would group them up, and add the groups together. The calculation would then become 30 groups of 60. This grouping, for the purpose of repeated addition, is the multiplication process at its core. 30 groups of 60 is written as \(30\times 60=1,800\). So 1,800 kernels are required to fill up 30 bags of popcorn.
Both addition and multiplication are commutative, because the order does not affect the answer. 30 groups of 60 gets us the same result as 60 groups of 30.
\((30\times 60)=(60\times 30)\)
Our last operation, division, can be considered multiplication’s opposite. When we use division, we are essentially splitting up a large group into smaller subgroups. For our popcorn example, we can use division to answer the following question:
How many bags of popcorn can I make using 1,800 kernels if each bag requires 60 seeds?
This situation requires us to divide the large value 1,800 into groups of 60. Each smaller subgroup will now represent a bag of popcorn. 1,800 divided into groups of 60 is represented as \(1,800\div 60\). In this case, the answer is 30, so 30 bags of popcorn can be made with our 1,800 kernels. As you can see, division is not commutative because the order of the values plays a crucial role in determining the answer. \(1,800\div 60\) is not the same thing as \(60\div 1,800\).
Okay, that’s all for this review of the mathematical operations! Thanks for watching, and happy studying!
Mathematical Operation Practice Questions
The answer to a subtraction problem is called the …
A is the correct answer. Since subtraction is the difference between a smaller number and a larger number, the answer to a subtraction problem is called the difference.
Which statement is true?
D is the correct answer. Division splits a large group into smaller subgroups and multiplication is repeated addition of smaller subgroups to find the total in the large group. Therefore, these operations perform opposite functions.
Jamie rents a bicycle for $8 per hour. He has the bicycle for 4 hours altogether. Which equation can be used to find out how much money Jamie spends to rent the bicycle?
C is the correct answer. Since Jamie spends $8 for every hour he has the bicycle, he is spending $8 + $8 + $8 + $8, which is equal to $8 ✕ 4, or 32 dollars.
Which statement best illustrates the commutative property?
B is the correct answer. The commutative property states that the numbers in a math problem can be moved or swapped and the outcome of the equation will not change. The commutative property applies to addition and multiplication but does not work for division or subtraction.
At Mike’s Deli, the price for deli turkey is $4 per pound. Kate is buying turkey to make sandwiches for a luncheon. If Kate spends $80, which equation represents how many pounds of turkey she bought?
C is the correct answer. Kate knows that the total amount spent was $80. She also knows that each pound cost her $4. Kate needs to know how many equal groups $80 is split into if there is $4 in each group. To solve this problem, Kate needs to divide. Since 80 is the number that is being split up, it comes first in the division problem. B is incorrect because \(4÷80\) is not the same as \(80÷4\).
