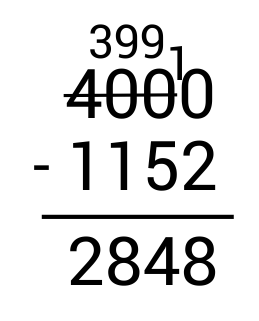Hey guys! Welcome to this video on subtracting large numbers.
I’m assuming you all know how to subtract smaller numbers, like \(9-2\), at this point. Since, now you are venturing on to learn how to subtract large numbers.
Well, good news! It is the exact same method, the numbers just get harder to do in your head. So, learning helpful methods to subtract large numbers will help save you some trouble.
Let’s look at a few different examples.
Example #1
We’ll start smaller.

Now, the first thing you need to make sure of, when subtracting large numbers, is that your number places are lined up correctly.
For instance, in our example here, 7 and 9 are both in the ones place, so they need to be lined up directly across from one another.
When you try to subtract 9 from 7 that will give you a negative number, which we can’t have because we know 27 is bigger than 9. So, we need to borrow from our next place value over here, which is in the tens place.
So to do that, we will subtract 1 from our 2, which is going to leave us with a 1 here, and bring that one down in front of our 7 to give us 17. So now we have 9 being subtracted from 17. Which gives us 8, so we bring our 8 down. Again, we want to keep our number place values aligned.
Now, we can imagine that there is a 0 here to the left of our 9. Which means that we aren’t subtracting anything from the 1 we have left over, so we can just go ahead and bring that 1 down.
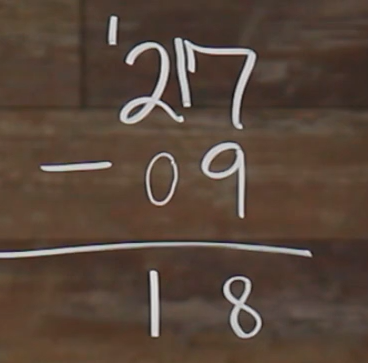
So, that gives us 18 as our answer, a really spaced apart 18.
Example #2
Let’s try something a little harder.
Let’s take 567 and take 98 away from it.
So, don’t forget, we need to line up our number places correctly.
So, we have 567, and now as I write out my 98, I need to make sure to keep my place value. So if it’s 98, that’s going to be in our tens place and our 8’s gonna be in our ones place, and we’re subtracting so we need that.
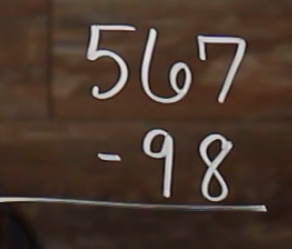
So, like in our last example, we are trying to take something bigger away than what we have here. So we need to borrow from our sweet neighbor 6 here. Which means we’re taking 1 away from it, so we cross out the 6 and that gives us 5 left over. And we’re gonna bring down that 1 in front of our 7.
Now, we have \(17-8\), which is 9. So again, keeping our number places aligned, we bring that down to our ones place. Now at this point, we are only worried about everything going on with our tens place. We only subtract numbers from their corresponding place values.
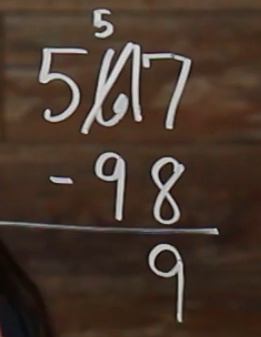
So, now we have \(5-9\). Since 9 is more than 5, we need to borrow from our hundreds place, so from our 5 over here. So we need to take 1 away from 5, so cross that out, that gives us 4. And we’re bringing that 1 in front of our 5 here because remember, we already borrowed 1 from the 6 and had a 5 left over.
Okay, now we have \(15-9\), which, is 6. So we need to carry that 6 down right here in our tens place, or to the left of our 9. So write a 6 right there. So, since we aren’t taking anything away from our 4 in our hundreds place here, we can just carry that 4 down, giving us our answer, which is 469
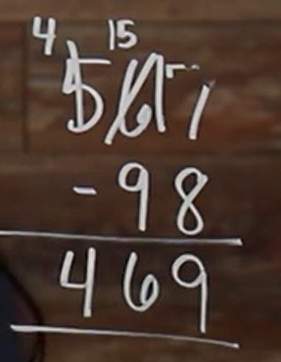
Example #3
Now, for our last example let’s take a look at how to borrow across zeros. I’ll show you what I mean.
Let’s take 3,001 and take away 999 from it.
So that’s, remember aligning all our place values, one’s place, subtract, boom!
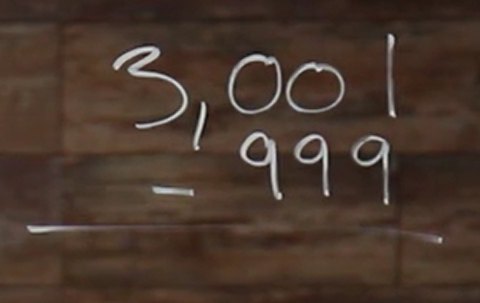
So we know we can’t take 9 away from our 1 here without giving us a negative number, so we need to borrow. But, when we go to borrow in our tens place we have a 0, we have nothing to take from. And that’s the same case with our hundreds place. So, what ends up happening is we’re taking 1 away from this 300 right here; so \(300-1=299\). So we can cross this out and we’ll take the 1 that we borrowed and bring it in front of our 1 here to give us 11.
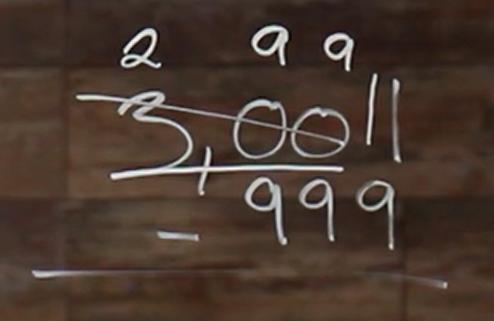
So now we have 9 being subtracted from 11, which is 2. So we carry down that 2.
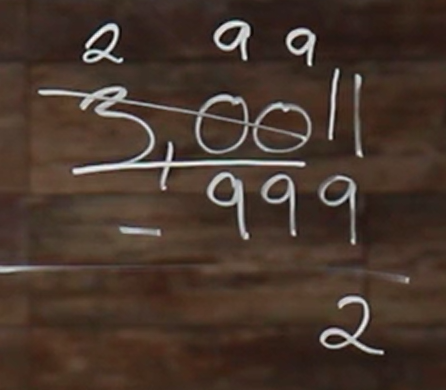
Then, when we go over to our next place, we have \(9-9=0\), and another \(9-9=0\). So we can just carry both of those 0s down. 0 and 0.
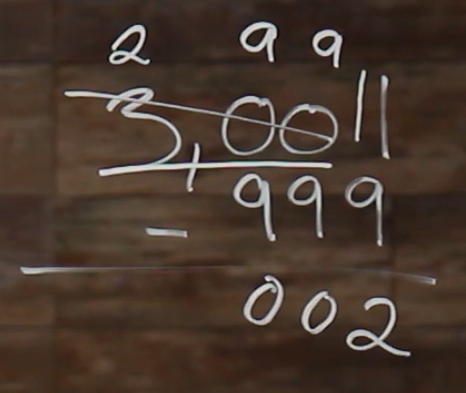
So now we are left with 2 in the thousands place, but we aren’t taking anything away from it, so we can just bring that down, giving us 2,002 as our answer.
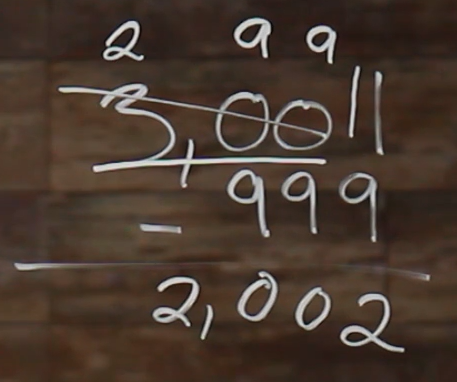
This borrowing works with all subtraction, just remember to only subtract numbers from their corresponding place values, and cross out and write the new number when you borrow. This will help you to follow your own work, and to minimize making mistakes.
I hope this helps! Don’t forget to subscribe to our channel below for further help! See you next time!
Subtracting Large Numbers Practice Questions
Subtract: \(503-67=\)
First, write the subtraction problem vertically, making sure to line up the numbers according to place value.
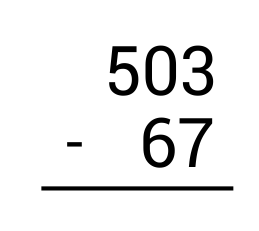
Start by subtracting the ones column on the right. Since \(3-7\) results in a negative number, we need to borrow from the tens place. However, there is a 0 in the tens place so there is nothing to borrow from. In this case, borrow from the tens and hundreds place. Cross out 50 and replace it with 49 since we are taking 1 away.
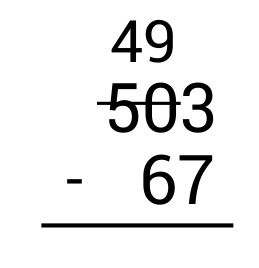
Next, write the borrowed 1 in front of the 3 in the ones place to get 13. Since \(13-7=6\), write 6 in the ones place as part of the answer.
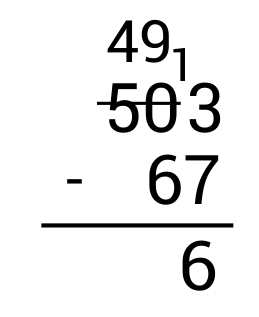
From here, move to the tens column and subtract. Since \(9-6=3\), write 3 in the tens place as part of the answer.
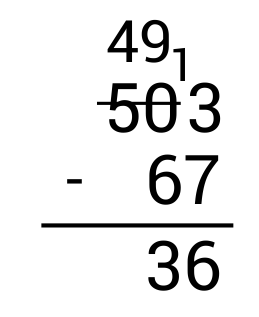
Finally, look at the hundreds column. Since there is a 4 with nothing below it, bring it down to the hundreds place as part of the answer.
\(503-67=436\)
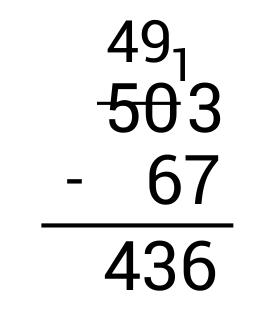
Subtract: \(932-778=\)
First, write the subtraction problem vertically, making sure to line up the numbers according to place value.

Start by subtracting the ones column on the right. Since \(2-8\) results in a negative number, we need to borrow from the tens place. Cross out the 3 in the tens place and make it a 2 since we are taking 1 away.
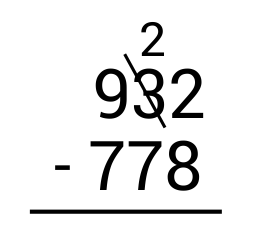
Next, write the borrowed 1 in front of the 2 in the ones place to get 12. Since \(12-8=4\), write 4 in the ones place as part of the answer.
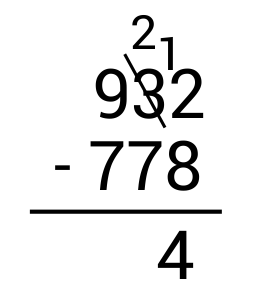
From here, move to the tens column and subtract. Since \(2-7\) results in a negative number, we need to borrow from the hundreds place. Cross out the 9 in the hundreds place and make it an 8 since we are taking 1 away.
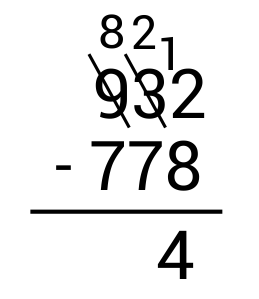
Next, write the borrowed 1 in front of the 2 in the tens place to get 12. Since \(12-7=5\), write 5 in the tens place as part of the answer.
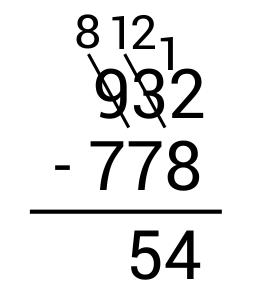
Finally, look at the hundreds column. Since \(8-7=1\), write 1 in the hundreds place as part of the answer.
\(932-778=154\)
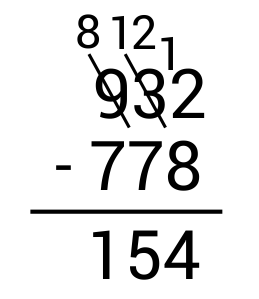
Subtract: \(600-281=\)
First, write the subtraction problem vertically, making sure to line up the numbers according to place value.
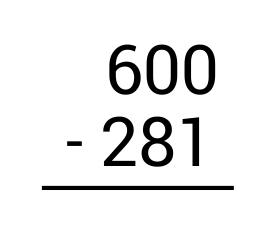
Start by subtracting the ones column on the right. Since \(0-1\) results in a negative number, we need to borrow from the tens place. However, we see there is a 0 in the tens place so there is nothing to borrow from. In this case, we borrow from the tens and hundreds place. Cross out 60 and replace it with 59 since we are taking 1 away.
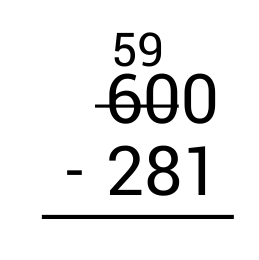
Next, write the borrowed 1 in front of the 0 in the ones place to get 10. Since \(10-1=9\), write 9 in the ones place as part of the answer.
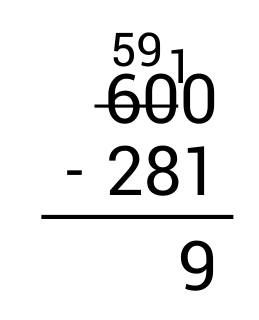
From here, move to the tens column and subtract. Since \(9-8=1\), write 1 in the tens place as part of the answer.
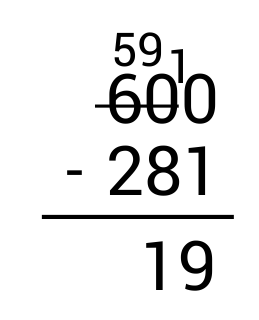
Finally, look at the hundreds column. Since 5 – 2 = 3, write 3 in the hundreds place as part of the answer.
\(600-281=319\)
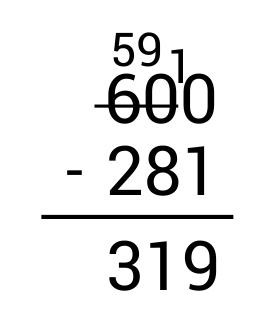
Matthew scored 5,020 points in the first round of a new video game. In the second round, he lost 721 points. How many points did he have left after the second round?
First, write the subtraction problem vertically, making sure to line up the numbers according to place value.
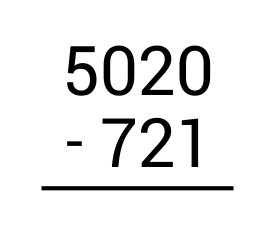
Start by subtracting the ones column on the right. Since \(0-1\) results in a negative number, we need to borrow from the tens place. Cross out 2 and replace it with 1 since we are taking 1 away.
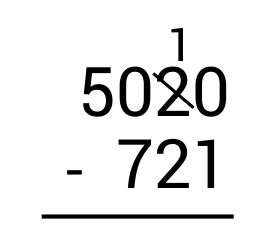
Next, write the borrowed 1 in front of the 0 in the ones place to get 10. Since \(10-1=9\), write 9 in the ones place as part of the answer.
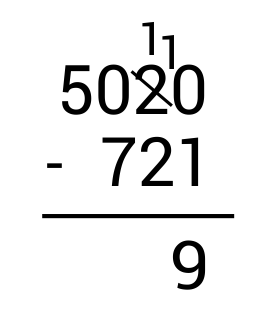
From here, move to the tens column and subtract. Since \(1-2\) results in a negative number, we need to borrow from the hundreds place. However, we see there is a 0 in the hundreds place so there is nothing to borrow from. In this case, we borrow from the hundreds and thousands place. Cross out 50 and replace it with 49 since we are taking 1 away.
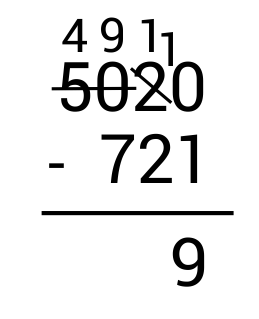
Next, write the borrowed 1 in front of the 1 in the tens place to get 11. Since \(11-2=9\), write 9 in the tens place as part of the answer.

From here, move to the hundreds column and subtract. Since \(9-7=2\), write 2 in the hundreds place as part of the answer.

Finally, look at the thousands column. Since there is a 4 with nothing below it, bring it down to the thousands place as part of the answer.
\(5,020-721=4,299\)

A cargo ship carries shipping containers that are two different sizes. 1,152 containers are 40-foot shipping containers, and the rest are 20-foot containers. If there are 4,000 containers aboard the ship altogether, how many of them are 20-foot containers?
First, write the subtraction problem vertically, making sure to line up the numbers according to place value.
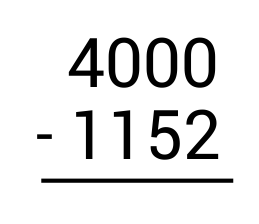
Start by subtracting the ones column on the right. Since \(0-2\) results in a negative number, we need to borrow from the tens place. However, we see there is a 0 in the tens place so there is nothing to borrow from. In this case, we look at the hundreds place. Since there is a 0 here as well, we look at the thousands place. Cross out 400 and replace it with 399 since we are taking 1 away.

Next, write the borrowed 1 in front of the 0 in the ones place to get 10. Since \(10-2=8\), write 8 in the ones place as part of the answer.
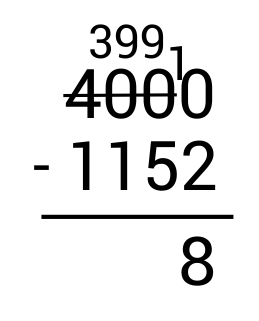
From here, move to the tens column and subtract. Since \(9-5=4\), write 4 in the tens place as part of the answer.
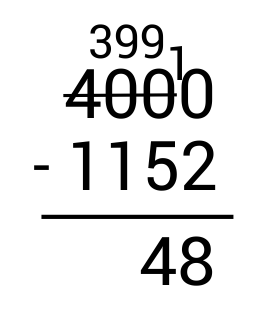
Now move to the hundreds column and subtract. Since \(9-1=8\), write 8 in the hundreds place as part of the answer.
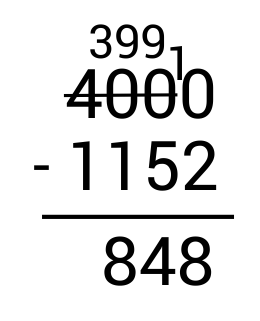
Finally, look at the thousands column. Since \(3-1=2\), write 2 in the thousands place as part of the answer.
\(4,000-1,152=2,848\)