Free Multiplication Charts and Worksheets

12 Times Table

×	1	2	3	4	5	6	7	8	9	10	11	12
1	1	2	3	4	5	6	7	8	9	10	11	12
2	2	4	6	8	10	12	14	16	18	20	22	24
3	3	6	9	12	15	18	21	24	27	30	33	36
4	4	8	12	16	20	24	28	32	36	40	44	48
5	5	10	15	20	25	30	35	40	45	50	55	60
6	6	12	18	24	30	36	42	48	54	60	66	72
7	7	14	21	28	35	42	49	56	63	70	77	84
8	8	16	24	32	40	48	56	64	72	80	88	96
9	9	18	27	36	45	54	63	72	81	90	99	108
10	10	20	30	40	50	60	70	80	90	100	110	120
11	11	22	33	44	55	66	77	88	99	110	121	132
12	12	24	36	48	60	72	84	96	108	120	132	144

Select a number!

Multiplication Chart Printables

For extra practice, we’ve provided several free printable times table charts below! Whether you need a standard multiplication chart, a blank multiplication chart, or a chart filled with color, these times table practice sheets are available (for free!) to be used and shared in classrooms and study groups to allow students to improve their multiplication skills.

Printable 12×12 Times Tables

 

Printable 10×10 Times Tables

 

Printable 8×8 Times Tables

 

Other Printable Times Tables

Multiplication Worksheets

Below, you’ll find some free multiplication worksheets, ranging from 3rd-grade to 5th-grade learning levels. These multipage multiplication worksheets are available to be used and shared freely in classrooms and study groups to allow students to improve their multiplication skills. We’ve also provided answer keys for each worksheet.

3rd Grade Multiplication Worksheets

 

4th Grade Multiplication Worksheets

 

5th Grade Multiplication Worksheets

How to learn multiplication tables

Mastering multiplication tables is part of the foundation for math fluency and understanding. Some of the best strategies for learning the times tables include the following:

What is multiplication?

Before learning the times tables, it’s necessary to understand how multiplication works.

Multiplication is the same thing as repeated addition. For instance, \(5 times 4\) is the same as adding the number 5 four times, or \(5+5+5+5\). Since \(5+5+5+5=20\), \(5 times 4\) is also equal to 20.

 
Knowing that multiplication is repeated addition makes it seem a bit less intimidating.

Use visuals

Another way to learn multiplication tables is to use visual models. These can help you to see and understand what the multiplication problems mean.

Some helpful visuals for multiplication are hands-on manipulatives and dot arrays.

When you comprehend the math, the times tables become easier to learn.

Break it down into smaller chunks

Instead of trying to memorize all the times tables at once, break it down into smaller chunks. Focus on one row or column of the times table chart at a time. Doing so makes the process of learning and memorizing these facts much more manageable.

Look for patterns

As you study each row of the multiplication chart, look to see what patterns you notice. Since multiplication is the same as repeated addition, you’ll see that each row follows a pattern in skip-counting. Becoming aware of these patterns will help you to learn the multiplication tables in no time.

Use easier facts to solve harder facts

It’s no secret that some multiplication facts are easier to figure out than others. The good news is that we can use the facts we know to help us solve the ones that we’re stuck on.

For example, consider \(6 times 7\).

 
Since this problem may be more difficult to commit to memory, we can use an easier fact, such as \(5 times 7\), to help us solve it. Since most of us are already familiar with skip-counting by 5s, we can start here. Five groups of 7 equals 35, and 6 groups of 7 is just one more set of 7.

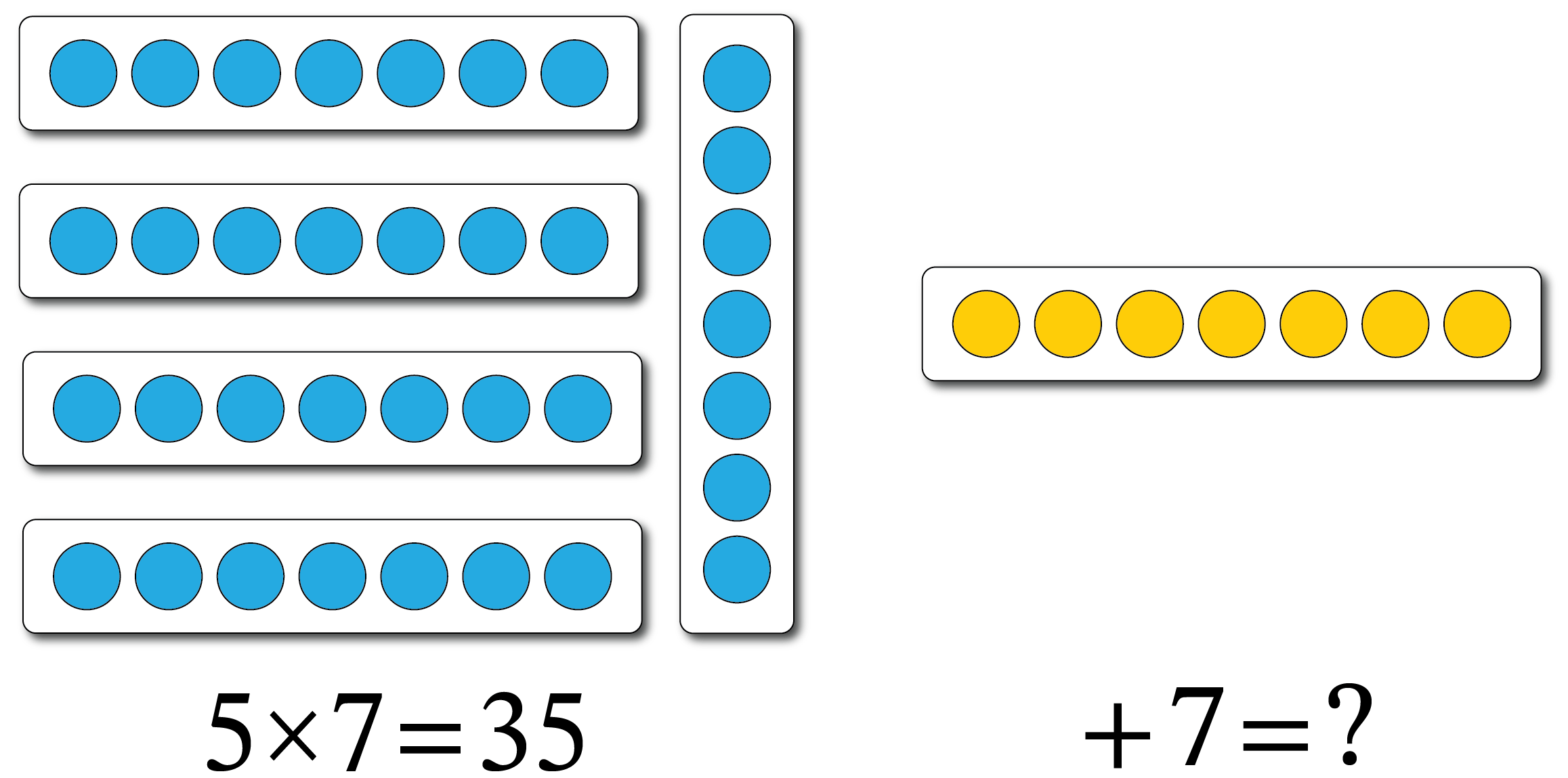
Since \(35+7=42\), \(6 times 7\) is also equal to 42.

In most cases, an easier math fact can be used as a stepping stone to help solve a more challenging problem.

Study, study, study!

Learning all the multiplication tables takes time. It’s helpful to practice with consistency and study using a times table chart. The times table chart, or multiplication chart, is a great tool to help with memorization.

The most important thing to keep in mind is that learning these facts won’t happen overnight. Instead, set aside a few minutes each day to review a portion of the times table chart using some of the strategies mentioned above.

How to memorize multiplication tables

Once you understand how multiplication works, you’re ready to work on memorization. Committing something to memory takes time, repetition, and practice. Let’s go over some of the most effective ways to memorize the times tables.

Practice skip-counting

Each row or column on a multiplication chart follows a pattern that can be learned by skip-counting. Skip-counting means counting forward or backward by any number that is not 1.

For example, skip-counting by 2s is 2, 4, 6, 8, 10, and so on.

Skip-counting by 5s is 5, 10, 15, 20, 25, 30, etc.

Practicing this skill with the numbers 2 through 12 will help you commit the times tables to memory.

Recite forward and backward

For many people, saying the multiplication tables aloud helps with memorization. Reciting the times tables also reinforces how each of the products is related. For instance, reciting “\(4 times 1\) is 4. \(4 times 2\) is 8. \(4 times 3\) is 12…” will help remind you that each subsequent product is found by adding 4 each time.

Likewise, reciting the 4s times table backward (“\(4 times 12\) is 48, \(4 times 11\) is 44,…”) will help show that each subsequent product is found by subtracting 4 each time.

Reciting times tables forward and backward helps with memorization and making connections.

Flashcards

There are lots of ways to use flashcards to help you commit the multiplication tables to memory. Below are some suggestions:

• Without looking at the answers, order a set of flashcards from the lowest to the highest product.
• Select a flashcard and draw a visual, such as a dot array, to represent the math fact.
• Choose a flashcard and write down another multiplication problem that gives the same product. For instance, \(6×2=12\) and \(2×6=12\).
• Review your flashcards and separate them into two groups: those you know and those you don’t know. Spend a few extra minutes going over the flashcards you don’t know yet.

Games

Who said memorizing the times tables had to be boring? There are lots of games and activities that can help make it fun.

For instance, using a deck of cards, you and a friend can play Multiplication War. Here’s how you play:

1. Each player is given exactly half the deck of cards, face-down.
2. Each player draws the top card from their respective piles and places it face-up.
3. The first player to multiply the amounts shown on each player’s card wins that round and takes both cards.
4. The player with the most cards at the end wins the game!

 

Songs

Catchy multiplication songs are a great way to get some of those facts to stick in your brain. Since everyone’s learning style is different, some people may be able to memorize faster with music. If you’re feeling extra creative, you can even write a multiplication song of your own!

Quiz yourself

Once you feel like you’re getting the hang of memorizing the times tables, it’s time to test your knowledge. Quiz yourself regularly, but don’t overdo it. If you want, ask a friend or an adult to help you with this. Remember to be patient with yourself.

Learning the multiplication tables is a process. The best way to commit them to memory is to review, repeat, and reinforce over time. Quizzing yourself (or having someone help you) for a few minutes each day will go a long way.
 
 

---

As we mentioned earlier, multiplication facts are filled with patterns. Recognizing these patterns will help with memorization. Here are the times tables with the easiest patterns to spot:

Multiplying by Zero

Any number multiplied by 0 results in a product of 0. This concept is called the Zero Product Property. Since 0 times any number is always 0, you don’t even have to worry about memorizing this times table.

Multiplying by 1

Any number multiplied by 1 results in that number itself. For instance, \(7 times 1=7\), \(9 times 1=9\), and \(11 times 1=11\). This concept is called the Identity Property.

Multiplying by 2

Multiplying a number by 2 is simply doubling the number given, or adding that number to itself. For example, \(2 times 9\) means 2 sets of 9, or \(9+9\). Since \(9+9=18\), \(2 times 9\) is also 18. Once you recognize this pattern, this row on the times table chart becomes very easy to memorize.

Multiplying by 5

Most people recognize the pattern for the 5s times table, which is 5, 10, 15, 20, 25, etc. Each product ends in either a 0 or a 5.

Multiplying by 9

Even though they look tricky at first, the 9s times table also follows a pattern. For the products of 1 through 10, the number in the ones place goes down, and the number in the tens place goes up: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90.

Multiplying by 10

When multiplying any number by 10, add a 0 after that number to find the product. For instance, \(2×10=20\), since 2 with a 0 after it makes 20. Likewise, \(11×10=110\), because 11 with a 0 after it makes 110.

Multiplying by 11

There’s also a pattern in the 11s times table. When multiplying any number 1 through 9 by 11, repeat the digit two times. For example, \(6×11=66\). The product, 66, shows the number 6 repeated two times. Similarly, \(8×11=88\), and 88 shows the number 8 repeated twice.
 
 

---

A multiplication table, also called a multiplication chart or times table chart, looks like a grid of numbers. This grid can help you learn and memorize multiplication facts. Most times table charts are an 88 grid, which shows the multiplication tables up to 8, or a 12×12 grid, which shows the multiplication tables up to 12.

A times table chart can help you quickly calculate the solution to a multiplication problem. It’s also a great study tool to aid with memorizing multiplication facts.
 
 

---

Using a times table chart is easy. First, choose any number across the top. Next, select any number going down the left side. From here, follow the top number down its column to the point where it is in the same row as the number chosen on the left side of the grid. Follow the number on the left over to where this row intersects the selected column going down. They will meet at the product, which is the answer to the multiplication problem.

Let’s consider an example together. Here’s an 8×8 table to help us out:

×	1	2	3	4	5	6	7	8
1	1	2	3	4	5	6	7	8
2	2	4	6	8	10	12	14	16
3	3	6	9	12	15	18	21	24
4	4	8	12	16	20	24	28	32
5	5	10	15	20	25	30	35	40
6	6	12	18	24	30	36	42	48
7	7	14	21	28	35	42	49	56
8	8	16	24	32	40	48	56	64

Select a number!

Say you need to multiply \(8 times 7\). Start by finding the first factor, 8, in the top row going across. Next, find the second factor, 7, in the column on the left side of the times table chart. Follow the 8s column down to where it is in line with the 7s row going across. Trace these areas of the times table chart with your fingers if that helps. Since the column for 8 and the row for 7 meet at 56, the product of \(8 times 7\) is 56.

Another way to use a multiplication chart is as a study tool to help you memorize all the times tables. When studying, focus on one row or column of the chart at a time. Once you’ve mastered one times table, move on to another one. Before you know it, you’ll have the entire chart committed to memory.

Learning about and memorizing all the multiplication tables can be challenging, but there are many strategies to help you out. Remember that this process takes practice and time. Give yourself a few minutes each day to work on it, and you’ll be a multiplication whiz before you know it.
 

---