
Hey, guys! Welcome to this Mometrix video on multiplying decimals.
Multiplying decimals may seem like a daunting challenge, but in this video, we’ll show you the techniques you need to decimate this decimal dilemma.
Place Value
In order to understand decimals, you first have to understand place value. Every number has a value based on its place relative to the other numbers.
Let’s look at the number 1,762. Based on place value, the number to the far left has the largest value. In this case, the number farthest to the left is in the thousands place.
The second number farthest to the left, our 7, is in the hundreds place.
The third number, 6, is in the tens place.
And then our last number here, which is farthest to the right, is in the ones place.
Here’s another way to think of this:
Hundreds place: \(7\times 100=700\)
Tens place: \(6\times 10=60\)
Ones place: \(2\times 1=2\)
Total: \(1,762\)
So what we see when we do that, is we should be able to multiply whatever number is in a specific place value, we should be able to take that number and multiply it times its place value. So, in this case, it’s in the thousands place, so we should be able to multiply it by a thousand, multiply 7 by 100, 6 by 10, and then 2 by 1. And so again, we’re multiplying every number by its place value. And then when we add it all up, we should get the total, which is equal to our number.
So now, any number behind our last number, so in this case 2, is called the “tenths” place. And this is where decimals come into play.
Let’s look at 1,762.8. The .8 behind the number 2 equals \(\frac{8}{10}\) of one whole.
So that was a review of numbers and their place value. Let’s take a look at how to actually multiply decimals.
Multiplying Decimals
You multiply decimals just like you would normal whole numbers. The trick is understanding how and when to move the decimal point so you get the right answer.
We’ll use this equation to show how it’s done:
Remember place value. That means 45 and 18 hundredths multiplied by 0.5, or five-tenths. So let’s figure this out.
In solving the problem, pretend (for just a moment) that the decimal point isn’t there. That would give you this equation:
You don’t need the 0 since it doesn’t add anything to the equation. If we solve this equation, we get:
| \(4,518\) | |
| \(\times\)\(5\) | |
| \(22,590\) |
But we’re not done. We have to figure out where to place the decimal. Here’s how you do that.
Go back to the original equation and count how many numbers are behind each decimal point. In this case, there are three. Two here (45.18) and one here (0.5).
We’re almost done. Now that we know there are three numbers behind the decimals, we go back to our answer and place the decimal three places from the last number. So the first answer we got was 22,590. But remember, we have to move our decimal point three places to the left because we had 3 places behind our decimal points here. So when we do that, our decimal point ends up right after our 22.
So our final answer is 22.59.
So that’s our look at multiplying decimals. As you can see, the concept seems much harder than it actually is. If you understand place value and how to move the decimals in the right place, you’ll do just fine.
I hope this video was helpful! See you guys next time!
Frequently Asked Questions
Q
How do you multiply decimals?
A
Multiply decimals the same way you would multiply other numbers. Then, count how many digits are after the decimal points in the multiplier and multiplicand and put the decimal point in the product that many places from the end.
Ex. 1.4 × 0.23 =
Multiply as normal
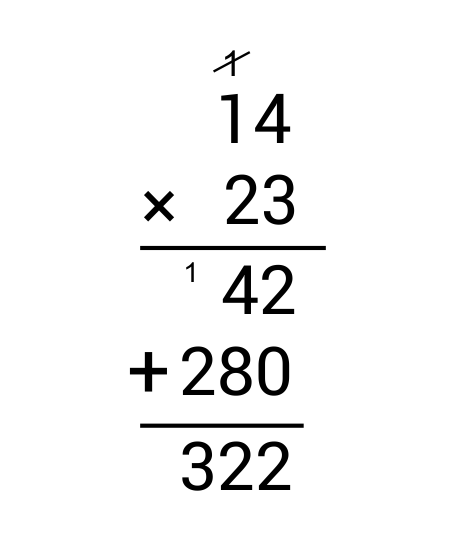
There is 1 digit after the decimal point in the multiplicand (1.4) and 2 digits after the decimal point in the multiplier (0.23). Move the decimal point in the product 3 (1 + 2) places from the end of the number: 0.322.
1.4 × 0.23 = 0.322
Q
How do you multiply decimals by whole numbers?
A
Multiply decimals by whole numbers the same way as with non-decimal numbers and then place the decimal point in the same place as in the original decimal number.
Ex. 1.74 × 13 =
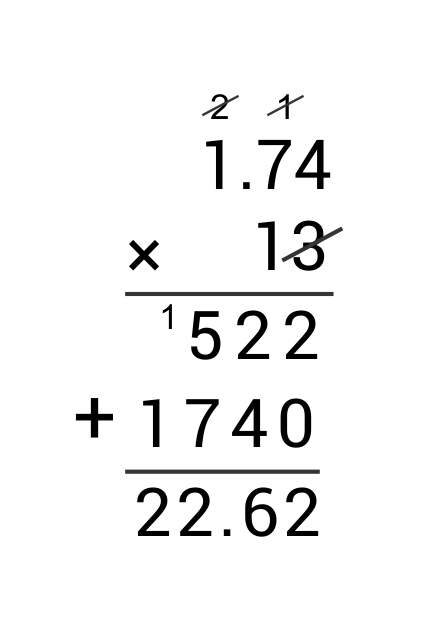
Q
How do you multiply repeating decimals?
A
Multiply repeating decimals by rounding the decimal number and then multiplying or turning it into a fraction and then multiplying fractions.
Ex. \(1.25×3.\overline{3}\)

Or
\(1.25=1 \frac{1}{4}=\frac{5}{4}\)
\(3.\overline{3}=3 \frac{1}{3}=\frac{7}{3}\)
\(\frac{5}{4}×\frac{7}{3}=\frac{35}{12}=2 \frac{11}{12}\)
Q
How do you multiply decimals without a calculator?
A
Multiply decimals without a calculator by first multiplying the numbers as regular whole numbers, then put the decimal in a place so that there are as many digits after the decimal point as there are in the original numbers combined.
Ex. 0.45 × 7.9
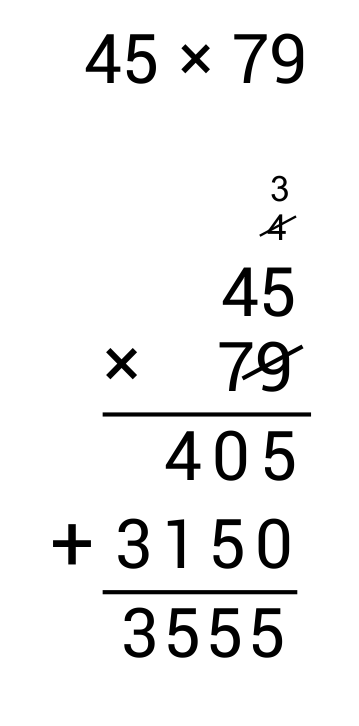
Since there are 3 (2 + 1 = 3) places after the decimals in the original numbers, have 3 places after the decimal in this number. The final answer is 3.555.
Multiplying Decimals Practice Questions
Represent the appropriate place value of each digit in the number 126.34.
The correct answer is \(1×100+2×10+6×1\)\(+3×0.1+4×0.01=126.34\).
1 represents 1 group of one hundred.
2 represents 2 groups of ten.
6 represents 6 groups of one.
3 represents 3 tenths.
4 represents 4 hundredths.
The last answer choice shows the correct place value for each digit of 126.34.
Calculate the product of \(62.5×1.3\).
The correct answer is 81.25. When multiplying decimal values, apply the standard algorithm for multiplication as though there are no decimals. In other words, calculate \(625×13\), which is equal to 8,125. Now, determine where to place the decimal point. In the original problem, 62.5 shows one decimal movement to the left, and 1.3 shows the same thing. This means that a total of two decimal movements to the left are needed to reach the final answer of 81.25.
Calculate the product of \(3.8×1.96\).
The correct answer is 7.448. When multiplying decimal values, apply the standard algorithm for multiplication as though there are no decimals. In other words, simply calculate \(38×196\), which is equal to 7,448. Now, determine where to place the decimal point. In the original problem, 3.8 shows one decimal movement to the left, and 1.96 shows two decimal movements to the left. This means that a total of three decimal movements to the left are needed to reach the final answer of 7.448.
Calculate the product of \(0.5×1.03\).
The correct answer is 0.515. When multiplying decimal values, apply the standard algorithm for multiplication as though there are no decimals. In other words, simply calculate \(5×103\), which is equal to 515. Now, determine where to place the decimal point. In the original problem, 0.5 shows one decimal movement to the left, and 1.03 shows two decimal movements to the left. This means that a total of three decimal movements to the left are needed to reach the final answer of 0.515.
Calculate the product of \(22×5.6\).
The correct answer is 123.2. When multiplying decimal values, apply the standard algorithm for multiplication as though there are no decimals. In other words, simply calculate \(22×56\), which is equal to 1,232. Now, determine where to place the decimal point. In the original problem, 22 shows no decimal movement to the left, and 5.6 shows one decimal movement to the left. This means that only one decimal movement to the left is needed to reach the final answer of 123.2.