Converting Decimals to Fractions and Percentages

Hello, and welcome to this video about converting decimals to fractions and percentages!

Today we’ll explore the connection between decimals, fractions, and percents. We’ll also talk about how to use these numbers in the real world.

Before we get started, let’s review a few things. First, a decimal is a number that has a whole number part and a fractional part. Separating these parts is a dot called a decimal point. The digits that come after the decimal point show a value that is less than 1.

For instance, in the number 25.16, 25 is the whole number part, and the fractional part is .16, which comes after the decimal point. In the number 0.75, the whole number part is 0, and the fractional part is .75. 0.75 is a decimal that is less than 1.

Decimals are based on powers of 10. As we move from left to right, each place value is divided by 10:

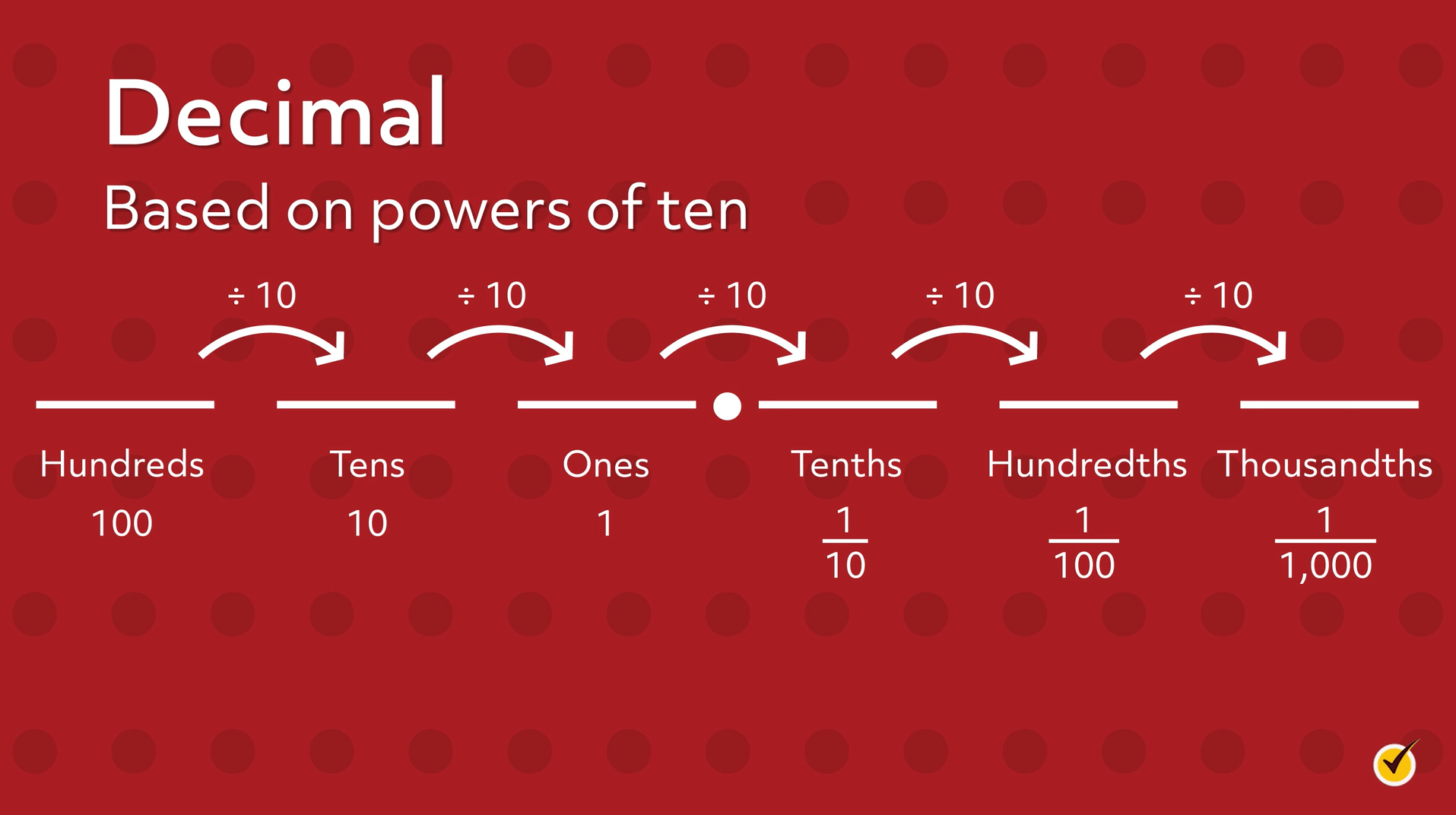
The decimal 5.25 is read as “five and twenty-five hundredths”. Since 25 comes after the decimal point, this is the fractional part of the number. We say “twenty-five hundredths” because the last digit, 5, is in the hundredths place.

The decimal 0.875 is read as “eight hundred seventy-five thousandths” because the last digit, 5, is in the thousandths place.

Since decimals contain fractional parts, they can also be written as fractions. Changing a decimal into a fraction is just a different way of expressing the same number. To convert a decimal into a fraction, write the numbers after the decimal point as the numerator and the place value as the denominator.

For example, in the number 0.7, there is a 7 in the tenths place. First, write the number after the decimal point as the numerator of the fraction: \(\frac{7}{}\). Next, look at the place value of the last digit in the decimal. Since 7 is the only decimal digit and it is in the tenths place, write 10 as the denominator of the fraction: \(\frac{7}{10}\).

In the number 0.6, the six is in the tenths place. The numerator is six, and the denominator is ten, so the fraction is \(\frac{6}{10}\). We can simplify \(\frac{6}{10}\) by dividing the numerator and denominator by 2 to get \(\frac{3}{5}\). The original fraction, \(\frac{6}{10}\), is referred to as the decimal fraction, and the simplified fraction, \(\frac{3}{5}\), is called the common fraction.

Let’s consider another example. Let’s convert 0.25 into a fraction. First, write the numbers after the decimal point, 25, as the numerator in the fraction: \(\frac{25}{}\)

Next, look at the place value of the digit 5. Since 5 is in the hundredths place, write 100 as the denominator of the fraction: \(\frac{25}{100}\).

The final step is to simplify the fraction if needed. Since 25 and 100 share a common factor of 25, we can simplify the fraction by dividing the numerator and denominator by 25: \(\frac{25\div 25}{100\div 25}=\frac{1}{4}\).

0.625 as a Fraction

Now it’s your turn. Convert 0.625 into a fraction. Pause this video, convert the decimal into a fraction, and don’t forget to simplify if needed. When you’re ready, resume the video, and we’ll go over everything together.

Now that you’ve tried this one yourself, let’s go over it together.

First, write the numbers after the decimal point, 625, as the numerator: \(\frac{625}{}\)

Next, look at the place value of the last digit, 5. Since 5 is in the thousandths place, write 1,000 as the denominator of the fraction: \(\frac{625}{1,000}\)

The final step is to simplify. Since 625 and 1,000 share a common factor of 25, we can simplify the fraction by dividing both numerator and denominator by 25: \(\frac{625\div 25}{1,000\div 25}=\frac{25}{40}\). Since 25 and 40 share a common factor of 5, divide again by 5: \( \frac{25\div 5}{40\div 5}=\frac{5}{8}\). Great job!

A percentage is a ratio that is expressed as a part out of 100. When written as a fraction, its denominator is always 100. Numbers with decimals can be expressed as percents. To convert a decimal to a percentage, multiply the decimal by 100 and write the percent sign (%) after the number.

Let’s look at an example together. Convert the decimal 0.25 into a percent. First, multiply 0.25 times 100. To multiply a decimal by 100, move the decimal point 2 spaces to the right. That gives us a product of 25. Therefore, 0.25 equals 25%.

Let’s try another one. Convert 0.5 into a percent. Remember, the first step is to multiply 0.5 by 100. When we do so, we move the decimal two spaces to the right. Notice that there are no digits in the hundredths or thousandths place in 0.5. In this case, we can rewrite 0.5 as 0.500, using the 0s as placeholders. When we move the decimal 2 spaces to the right, we get a product of 50.0, or 50. So 0.5 equals 50%.

Let’s look at one more example together. Convert 0.125 into a percent. Recall that the first step is to multiply the decimal by 100, which moves the decimal point 2 spaces to the right. This gives us a product of 12.5, so the percent is 12.5%.

Now it’s your turn. Convert 1.08 into a percent. Pause this video, convert the decimal, and don’t forget to write the percent sign next to it. When you’re ready, resume the video and we’ll go over the answer together.

Now that you’ve tried this one, let’s take a look at it. To convert 1.08 into a percent, multiply the decimal by 100. Since multiplying by 100 moves the decimal point 2 spaces to the right, 1.08 times 100 equals 108. Therefore, the equivalent percentage is 108%. Nice work!

Knowing how to convert fractions to decimals and percents is an important skill in the real world. Here are a few ways you may see fractions, decimals, and percents in your daily life:

• Shopping: When shopping, sales tax and coupons often use fractions, and other sale signs are often written in percents. Knowing how to calculate these will help determine the total cost of the items being purchased.
• Sports: In many sports like baseball and basketball, fractions are used to determine statistics such as shooting percentages.
• Restaurants: When going out to eat with a group of friends, you sometimes need to split the cost of the bill. To divide the total cost, you need to use fractions.
• Tests and exams: Scores of tests and exams are often expressed as fractions or percents.

Let’s look at some scenarios where we need to convert decimals to fractions or percentages. Consider the following word problems:

1 Canadian dollar is equivalent to 0.96 of a US dollar. What fraction of a US dollar is the Canadian dollar?

In 1947, Jackie Robinson’s batting average was .297. How can this be expressed as a percent?

Pause this video here and see if you can answer these questions yourself. When you’re ready, resume the video and we’ll go over the answers together.

Now that you’ve tried these problems, let’s go over them together.

1 Canadian dollar is equivalent to 0.96 of a US dollar. What fraction of a US dollar is the Canadian dollar?

To convert the decimal 0.96 into a fraction, start by writing the numbers after the decimal point, 96, as the numerator: \(\frac{96}{}\)

Next, look at the place value of the last digit, which is 6. Since 6 is in the hundredths place, the denominator is 100. Therefore, the decimal fraction is \(\frac{96}{100}\). 96 and 100 share a common factor of 4, so we can simplify the fraction by dividing both numerator and denominator by 4: \(\frac{96\div 4}{100\div 4}=\frac{24}{25}\). Therefore, 1 Canadian dollar is equal to \(\frac{24}{25}\) of a US dollar.

In 1947, Jackie Robinson’s batting average was .297. How can this be expressed as a percent?

First, multiply 0.297 by 100. Since multiplying by 100 moves the decimal point 2 spaces to the right, 0.297 times 100 equals 29.7. Jackie Robinson’s batting average can be expressed as 29.7%. As a batter, Jackie Robinson was successful almost 30% of the time.

Knowing how to convert decimals to fractions and percentages helps us understand mathematical aspects of everyday life. I hope this video on converting decimals to fractions and percentages was helpful. Thanks for watching, and happy studying!

Fact Sheet

Download Fact Sheet

Converting Decimals to Fractions and Percentages Practice Questions