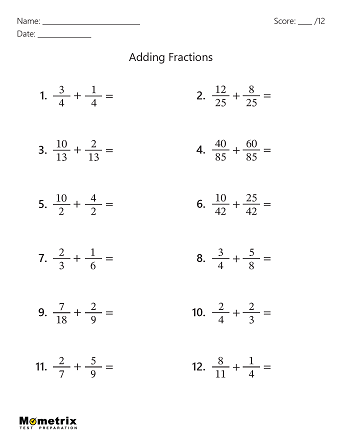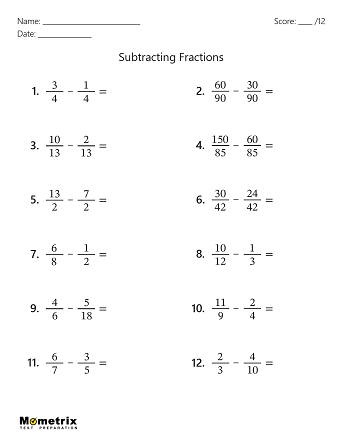Adding and Subtracting Fractions
Hi, and welcome to this video on adding and subtracting fractions!
Before we get into it, let’s review some terminology needed to understand the concepts.
A fraction is a ratio of values that reflect a “part” to a “whole.” The “part” is called the numerator and is written above the division line. The “whole” is referred to as the denominator and is written below the division line:
| numerator | ||
| denominator |
When combining fractions by addition or subtraction, the work is done only with the numerators. The denominator does not change. For example, suppose there were seven rolls in a basket on the dinner table. You ate one and your brother ate two. What is the fraction that represents the number of rolls that were eaten by you and your brother?
You can probably conceptualize this example of adding fractions pretty quickly. You simply add up the number of rolls eaten by you and your brother and divide by the total number of rolls that were on the table at the start of dinner. Remember, the denominator remains the same. \(\frac{1}{7}+ \frac{2}{7}\), which can be seen as \(\frac{1+2}{7}\), equals \(\frac{3}{7}\). The fraction \(\frac{3}{7}\) represents the number of rolls eaten by you and your brother.
\(\frac{1}{7}+\frac{2}{7}=\frac{1+2}{7}=\frac{3}{7}\)
Subtracting fractions can be thought of in the same way.
Let’s say you and your friends are playing a game of cards. You are holding three of the four kings that are in a deck of cards. You throw down the King of Hearts on the next play. What fraction represents the number of kings in your hand now?
Because there are a total of four kings in a deck of cards, the fraction, 34, represents the three kings that you had in your hand to start with. If you give away the King of Hearts, then the numerator of this fraction decreases by one. The fraction of the kings that you have in your hand changes as follows: \(\frac{3}{4}- \frac{1}{4}\), which can be seen as \(\frac{3-1}{4}\), equals \(\frac{2}{4}\), which simplifies to one half.
\(\frac{3}{4}-\frac{1}{4}=\frac{3-1}{4}=\frac{2}{4} \text{ or } \frac{1}{2}\)
These examples are pretty straightforward because the denominators of the fractions being added or subtracted are the same.
How to add Fractions with Different Denominators
If denominators are not the same, there is a bit more work involved. Specifically, one or both of the fractions must be algebraically adjusted to create common denominators.
Example:
\(\frac{2}{5}+\frac{3}{10}\)
Like I said before, these fractions cannot be added until they share a common denominator. In fact, the denominator must be the smallest value that both denominators can divide into evenly. This value is known as the least common denominator (LCD).
When considering the denominators 5 and 10, it becomes clear that 10 is the smallest number that both 5 and 10 can divide into evenly. This means that we will have to algebraically adjust the first fraction so that the denominator becomes 10. We do this by multiplying both the numerator and denominator. The rules for multiplying fractions require multiplying the numerator times the numerator and the denominator times the denominator: \(2 \times 2=4\) and \(2 \times 5=10\).
\(\frac{2}{2}\times \frac{2}{5}=\frac{4}{10}\)
This work creates the fraction \(\frac{4}{10}\), which is equivalent to the original fraction, \(\frac{2}{5}\). At this point, the fractions with common denominators can be added: \(\frac{4}{10}+ \frac{3}{10}\), which can be seen as \(\frac{4+3}{10}\), equals \(\frac{7}{10}\).
\(\frac{4}{10}+\frac{3}{10}=\frac{4+3}{10}=\frac{7}{10}\)
This last example requires you to adjust both fractions to achieve a common denominator. Let’s work through this one together, then I’ll give you one to try on your own.
How to subtract Fractions with Different Denominators
\(\frac{5}{8}-\frac{1}{6}\)
So, first things first: What is the least common multiple of 6 and 8? 24. Because 24 divided by 8 is 3, we will have to adjust the first fraction by multiplying both the numerator and denominator by 3. \(24 \div 6=4\), so we will have to multiply the numerator and denominator of the second fraction by four.
\(\frac{3}{3} \times \frac{5}{8}-\frac{4}{4} \times \frac{1}{6}\)
These adjustments create equivalent fractions that have a common denominator of 24. Once that is taken care of, the numerators can be subtracted as follows:
\(\frac{15}{24}-\frac{4}{24}=\frac{11}{24}\)
Alright, now here’s one for you to try. Pause the video and see if you can solve it.
\(\frac{3}{5}+\frac{3}{7}\)
How did you do? Let’s walk through it. The least common multiple of 5 and 7 is 35. Adjust the first fraction by multiplying the numerator and denominator by 7, and adjust the second fraction by multiplying the numerator and denominator by 5. Once the denominators match, add the numerators. This gives us \(\frac{36}{35}\)!
\(\frac{7}{7} \times \frac{3}{5}+\frac{5}{5} \times \frac{3}{7}\) \(\frac{21}{35}+\frac{15}{35}=\frac{36}{35}\)
Let’s recap before we go. Whether you are adding or subtracting fractions, remember that the denominator will always stay the same, and sometimes, you will have to create a common denominator and find the least common multiple before you can proceed with the problem.
I hope this review was helpful! Thanks for watching and happy studying!
Frequently Asked Questions
Q
When adding fractions, do you add the denominator?
A
No, when adding fractions, you must first find a common denominator and convert both fractions to that denominator. Then add the numerators and keep the denominator.
Ex. \(\frac{1}{3}+\frac{1}{2}=\frac{1}{3}×\frac{2}{2}+\frac{1}{2}×\frac{3}{3}=\frac{2}{6}+\frac{3}{6}=\frac{5}{6}\)
Q
How do you add fractions with different denominators?
A
To add fractions with different denominators, first convert both fractions to a common denominator. Then, add the numerators and leave the denominator the same.
Ex. \(\frac{1}{3}+\frac{3}{4}=\frac{1}{3} (\frac{4}{4})+\frac{3}{4} (\frac{3}{3})=\frac{4}{12}+\frac{9}{12}=\frac{13}{12}=1 \frac{1}{12}\)
Q
What does adding similar fractions mean?
A
Adding similar fractions means adding fractions with the same denominator.
Ex. \(\frac{1}{4}+\frac{2}{4}=\frac{3}{4}\)
Q
Can you cross cancel when adding fractions?
A
No, you cannot cross cancel when adding fractions. Cross canceling only works with multiplying fractions.
Q
How do you subtract fractions?
A
To subtract fractions, convert both fractions to a common denominator. Then, subtract the numerators and leave the denominator the same.
Ex. \(\frac{4}{5}-\frac{1}{3}=\frac{4}{5} (\frac{3}{5})-\frac{1}{3} (\frac{5}{5})=\frac{12}{15}-\frac{5}{15}=\frac{7}{15}\)
Q
How do you subtract fractions with whole numbers?
A
Subtract fractions with whole numbers by turning the whole number into a fraction, converting to common denominators, subtracting, and simplifying if necessary.
Ex. \(4-\frac{5}{7}=\frac{4}{1}-\frac{5}{7}=\frac{4}{1} (\frac{7}{7})-\frac{5}{7}=\frac{28}{7}-\frac{5}{7}=\frac{23}{7}=3 \frac{2}{7}\)
Q
How do you subtract fractions with different denominators?
A
To subtract fractions with different denominators, first convert the fractions to ones with common denominators and then subtract the numerators, keeping the denominator the same.
Ex. \(\frac{4}{7}-\frac{1}{3}=\frac{4}{7} (\frac{3}{3})-\frac{1}{3} (\frac{7}{7})=\frac{12}{21}-\frac{7}{21}=\frac{5}{21}\)
Adding and Subtracting Fractions Practice Questions
Add the following fractions: \(\frac{1}{5}+\frac{3}{5}=\)
The correct answer is \(\frac{4}{5}\). When adding fractions that have the same denominator, simply add the numerators and keep the denominator the same. In this case, adding the numerators yields a sum of 4, and the denominator remains as 5. The result is \(\frac{4}{5}\).
Add the following fractions: \(\frac{12}{15}+\frac{2}{15}=\)
The correct answer is \(\frac{14}{15}\) . When adding fractions that have the same denominator, simply add the numerators and keep the denominator the same. In this case, adding the numerators yields a sum of 14, and the denominator remains as 15. The result is \(\frac{14}{15}\) .
Add the following fractions: \(\frac{2}{3}+\frac{1}{4}=\)
The correct answer is \(\frac{11}{12}\). There must be a common denominator in order to add these fractions. The common denominator will be the least common multiple of 3 and 4. The least common multiple of 3 and 4 is 12, so the fractions should be rewritten with 12 as the new denominator. Now, adjust the numerators. For the fraction \(\frac{2}{3}\), the denominator was multiplied by 4, so the numerator should also be multiplied by 4, which equals \(\frac{8}{12}\). For the fraction \(\frac{1}{4}\), the denominator was multiplied by 3, so the numerator should also be multiplied by 3, which equals \(\frac{3}{12}\). Finally, add \(\frac{8}{12}+\frac{3}{12}\) to get \(\frac{11}{12}\).
Add the following fractions: \(\frac{3}{7}+\frac{2}{5}=\)
The correct answer is \(\frac{29}{35}\). There must be a common denominator in order to add these fractions. The common denominator will be the least common multiple of 7 and 5. The least common multiple of 7 and 5 is 35, so the fractions should be rewritten with 35 as the new denominator. Now, adjust the numerators. For the fraction \(\frac{3}{7}\), the denominator was multiplied by 5, so the numerator should also be multiplied by 5, which equals \(\frac{15}{35}\). For the fraction \(\frac{2}{5}\), the denominator was multiplied by 7, so the numerator should also be multiplied by 7, which equals \(\frac{14}{35}\). Finally, add \(\frac{15}{35}+\frac{14}{35}\) to get \(\frac{29}{35}\).
Add the following fractions: \(\frac{5}{6}+\frac{1}{4}=\)
The correct answer is \(\frac{13}{12}\). There must be a common denominator in order to add these fractions. The common denominator will be the least common multiple of 6 and 4. The least common multiple of 6 and 4 is 12, so the fractions should be rewritten with 12 as the new denominator. Now, adjust the numerators. For the fraction \(\frac{5}{6}\), the denominator was multiplied by 2, so the numerator should also be multiplied by 2, which equals \(\frac{10}{12}\). For the fraction \(\frac{1}{4}\), the denominator was multiplied by 3, so the numerator should also be multiplied by 3, which equals \(\frac{3}{12}\). Finally, add \(\frac{10}{12}+\frac{3}{12}\) to get \(\frac{13}{12}\).
Subtract the following fractions: \(\frac{3}{4}-\frac{1}{4}\)
The correct answer is \(\frac{2}{4}\). When subtracting fractions that have the same denominator, simply subtract the numerators and keep the denominator the same. In this case, subtract 1 from 3 and then keep the denominator as 4. The result is \(\frac{2}{4}\).
Subtract the following fractions: \(\frac{5}{6}-\frac{2}{6}=\)
The correct answer is \(\frac{3}{6}\). When subtracting fractions that have the same denominator, simply subtract the numerators and keep the denominator the same. In this case, subtract 2 from 5 and then keep the denominator as 6. The result is \(\frac{3}{6}\).
Subtract the following fractions: \(\frac{5}{9}-\frac{1}{4}=\)
The correct answer is \(\frac{11}{36}\). Before these fractions can be subtracted, the denominators need to be the same. The least common multiple for 9 and 4 is 36, so change both denominators to 36. For the fraction \(\frac{5}{9}\), the denominator was multiplied by 4 to get 36, so the numerator needs to be multiplied by 4 as well. This gives us \(\frac{20}{36}\). For the fraction \(\frac{1}{4}\), the denominator was multiplied by 9 to get 36, so the numerator needs to be multiplied by 9. This gives us \(\frac{9}{36}\). Now, simply calculate \(20-9\) to get \(\frac{11}{36}\).
Subtract the following fractions: \(\frac{1}{2}-\frac{2}{5}=\)
The correct answer is \(\frac{1}{10}\). To begin, a common denominator must be found before these fractions can be subtracted. The least common multiple for 2 and 5 is 10, so change both denominators to 10. For the fraction \(\frac{1}{2}\), the denominator was multiplied by 5 to get 10, so the numerator needs to be multiplied by 5 as well. This gives us \(\frac{5}{10}\). For the fraction \(\frac{2}{5}\), the denominator was multiplied by 2 to get 10, so the numerator needs to be multiplied by 2. This gives us \(\frac{4}{10}\). Now, simply calculate 5-4 to get \(\frac{1}{10}\).
Subtract the following fractions: \(\frac{10}{12}-\frac{1}{6}=\)
The correct answer is \(\frac{8}{12}\). Like before, a common denominator must be found before these fractions can be subtracted. The least common multiple for 12 and 6 is 12, so change both denominators to 12. In this case, the fraction \(\frac{10}{12}\) will remain the same. For the fraction \(\frac{1}{6}\), the denominator was multiplied by 2 to get 12, so the numerator needs to be multiplied by 2. This gives us \(\frac{2}{12}\). Now, simply calculate \(10-2\) to get \(\frac{8}{12}\).
Worksheets
Use our free printable adding and subtracting fractions worksheets for additional practice!
