Proportional Change of Dimensions
Hi, and welcome to this video about proportional change of dimension! In this video, we will explore what it means to proportionally change dimension, how proportionally changing dimension affects measures of area in 2-D figures, and how proportionally changing dimension affects measures of volume in 3-D solids.
First, let’s recall what it means for two figures that are different sizes to be similar: They have the same shape, but their dimensions are proportional, which means they are different by a scale factor.
Consider these squares.
Their side lengths differ by a scale factor of 2 since each side of Square B is twice as long as each side of square A. So we can say that these figures are similar.
By contrast, these rectangles are not similar. The one on the right is twice as long as the one on the left, but their heights are the same. All lengths must differ by the same scale factor for the two figures to be proportional.
The question we are exploring is: “What happens to area and volume of similar figures when their dimensions change proportionally?” Well, let’s answer this by jumping back to our squares.
The area of Square A is 1 and the area of Square B is 4. Visually, this is what happens:
As you can see, four Square A’s can fit inside one Square B. In other words, even though Square B has 2 times the length and height of Square A, it has four times the area of Square A, not two times. Let’s look at Square C, with side length 3:
In this relationship, Square C contains nine Square A’s:
Now, there is actually a pattern to be found here. As we saw with Square A and Square B, the side lengths differed by a factor of 2 and the area differed by a factor of 4. With Square A and Square C, the lengths differed by a factor of 3 and the area differed by a factor of 9.
| When the side lengths differ by a factor of… | The area differs by a factor of… |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
How are 4 and 2 related? 2 x 2 = 4, but 4 is also equal to 22. Squaring makes sense, right, since area is measured in square units? On that note, 9 = 32. So it’s looking like we can just square the scale factor of the length to determine the scale factor of the area. So if our side lengths differ by a factor of 4, 42 = 16, so the area will differ by a factor of 16.
Let’s look at what’s going on here algebraically:
We know the area of a square is A = s2. Doubling the side lengths, we have A = (2s)2, which simplifies to 4s2. So, doubling the side lengths results in 4 times the area. When we triple the side lengths, the area is (3s)2, or 9s2 – nine times the original, as we saw earlier. Or, to put it another way, the area of a proportional figure equals (scale factor)2 times the area of the original figure.
Now, suppose one rectangle has area 6m2 and a similar rectangle has area 54m2. How much longer is each side of the large rectangle than the small one?
54 = (scale factor)2 x 6
9 = (scale factor)2
3 = scale factor
The sides of the large rectangle are 3 times the length of those of the small rectangle.
When we move from 2 to 3 dimensions, the effects are, well, similar! Let’s look at a quick example:
The large cube has edge lengths twice as long as the small cube.
But 8 small cubes fit inside the large cube. Since we’re talking about volume, we’re going to cube instead of square, so the volume of the large cube is 23 times the volume of the small cube. Otherwise, the big idea is the same as with area: the volume of a proportional figure equals (scale factor)3 x the volume of the original figure.
And that’s all there is to it! I hope this review was helpful. Thanks for watching, and happy studying!
Change of Dimension Practice Questions
Determine the scale factor that takes us from Rectangle X to Rectangle Y.
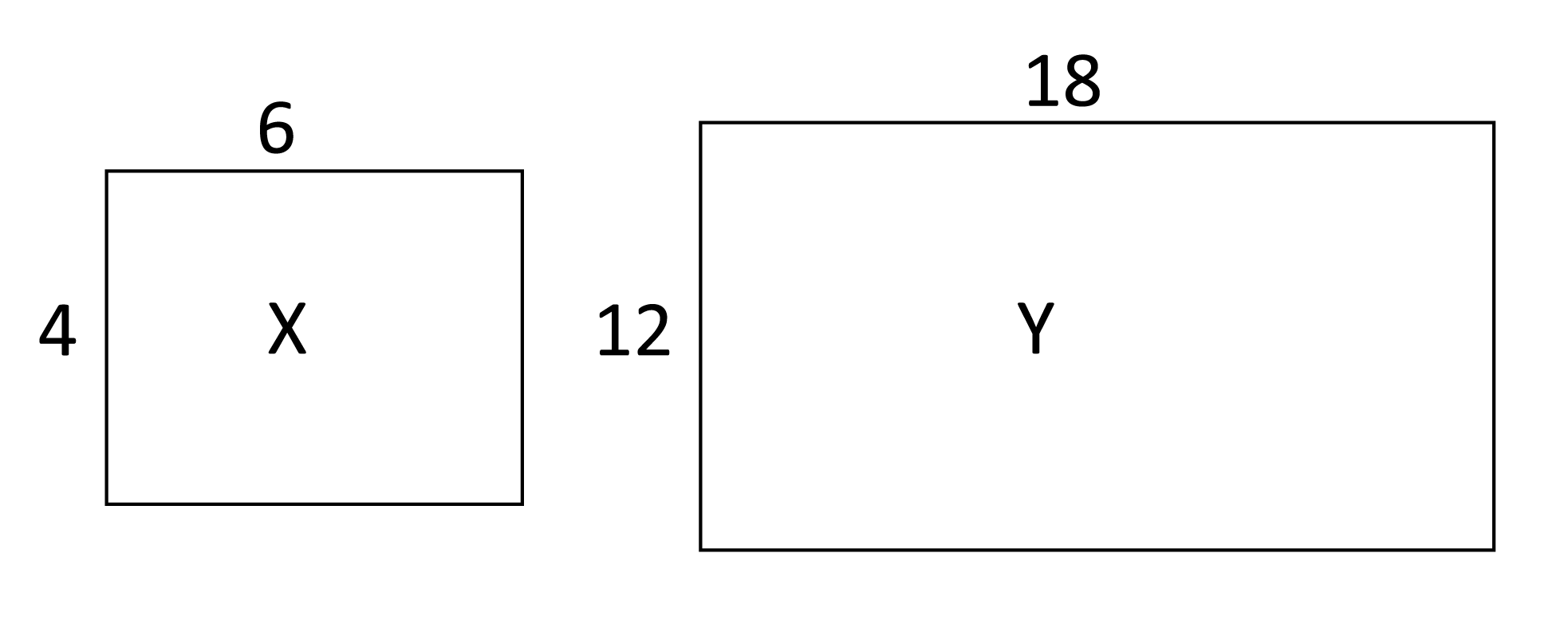
The scale factor is the ratio between corresponding measurements of an object. If the scale factor is a whole number, the copy will be larger. If the scale factor is a fraction, the copy will be smaller. The ratio of the heights is 4:12, which means that the height of Rectangle Y is three times taller than Rectangle X. The ratio of the lengths is 6:18, which means that the length of Rectangle Y is three times longer than Rectangle X. The scale factor is three because each side of Rectangle Y is three times that of Rectangle X.
What will happen to the surface area of the figure when the side lengths are increased by a scale factor of 4?
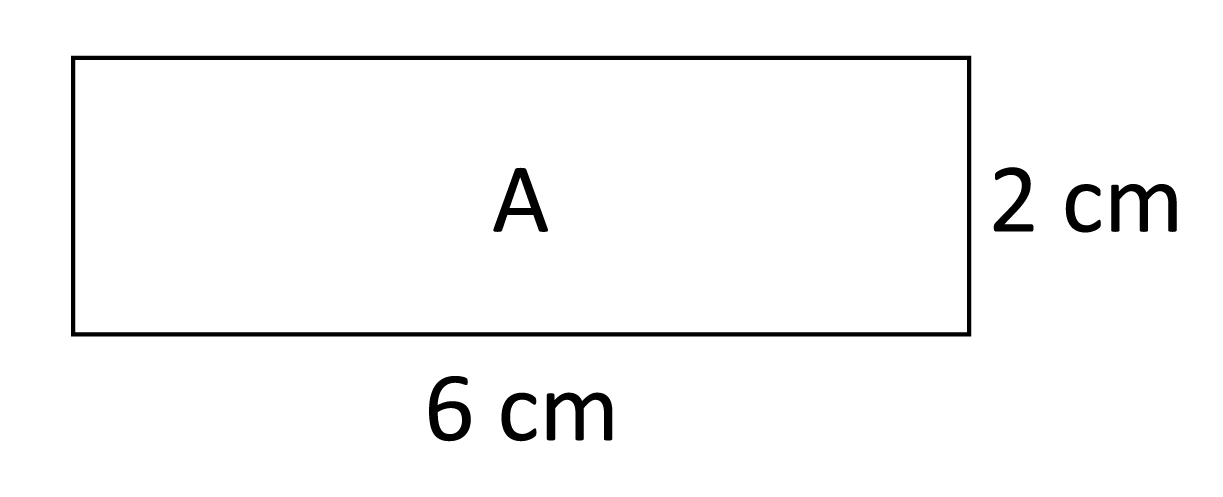
Squaring the scale factor of the side lengths will determine the scale factor of the areas. The side lengths of this shape are increased by a scale factor of 4; therefore, the area will be increased by a scale factor of \(4^2\), or 16. The new figure will have an area that is 16 times larger than the original figure.
What set of dimensions would create a rectangle that is “similar” to the rectangle below?
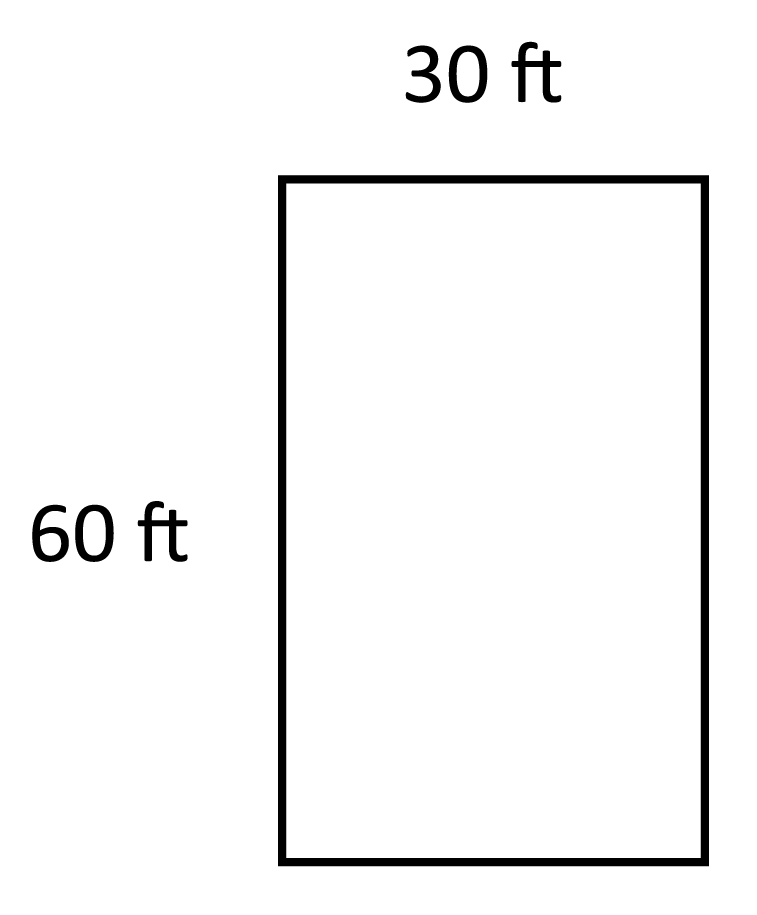
Shapes that are “similar” have congruent corresponding angles, and proportional side lengths. In order to create side lengths that are proportional, we need to multiply both the height and the width by the same number. In this example, multiplying the height and the width by \(\frac{1}{2}\) produces side lengths that are
proportional. 60 ft by 30 ft becomes 30 ft by 15 ft.
Mrs. Carson runs a concession stand at a movie theater. She has had many requests to create an extra large option for popcorn bags. Mrs. Carson agrees to start selling the jumbo size, and decides to double the dimensions of the current bag. The current bags are 7 inches tall, 4 inches wide, and 5 inches long. How will the volume of the new jumbo bags of popcorn compare to the smaller original bags?
The new jumbo size bag dimensions increase by a scale factor of 2. Each side length is now twice as large as the original size. We can cube this scale factor in order to see what the scale factor in volume will be. A scale factor of 2 cubed gives us 8, because \(2\times2\times2=8\). This means that the new volume of popcorn will be 8 times as large as the original volume!
Casey has a carton of juice that is 4 inches tall, 3 inches long, and 2 inches wide. If the dimensions were increased by a scale factor of 3, what would the new volume of juice be?
The original dimensions of the carton of juice were multiplied by a scale factor of 3. If we cube this scale factor, we will know the scale factor for the volume. 3 × 3 × 3 = 27, so the carton of juice will be increased by a scale factor of 27.
The original volume was 2 in × 3 in × 4 in which is 24 in3 . When this volume is multiplied by a scale factor of 27 we have 24 in3 × 27 = 648 in3 as the new volume.
