Converting Fractions into Decimals and Percentages
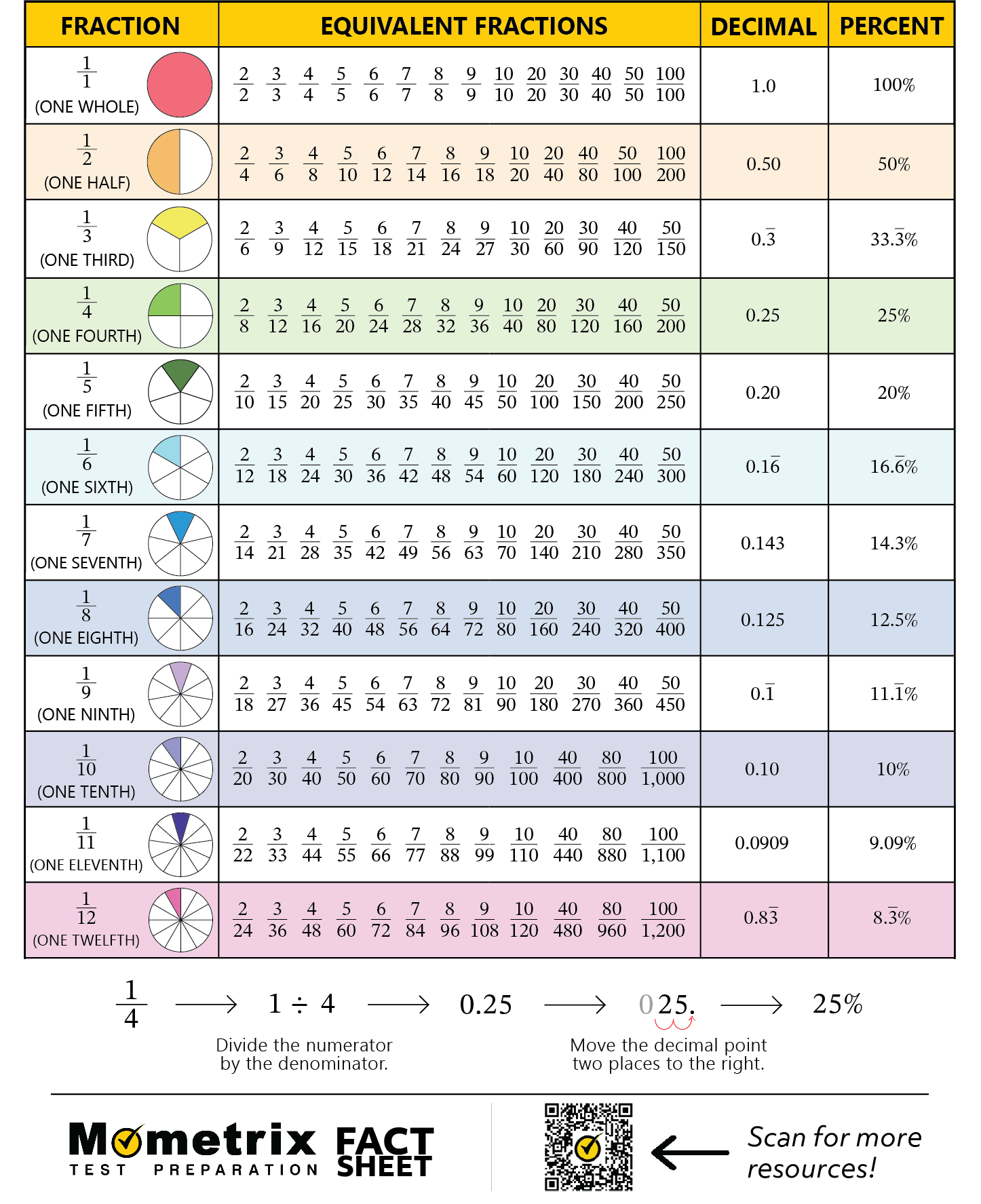
Hello and welcome to this video about converting fractions to decimals and percents! In this video, we will explore:
- How to visually convert fractions to decimals and percents and
- How to numerically convert fractions to decimals and percents
Before we get started, let’s review a couple of key concepts that we will use to help the math make sense.
Consider the fraction \(\frac{10}{10}\). One way to think about fractions is to think of them as division.
\(\frac{10}{10}=1\)
In other words, ten-tenths is one whole.
\(\frac{10}{10}\) can be written equivalently as \(\frac{100}{100}\). The fraction bar can be said as “per,” so this expression can be said as “100 per 100.” The word “percent” literally means “per 100,” so “100 per 100” means 100 percent.
Therefore, when the same number is divided by itself, the result as a decimal is 1 and as a percent is 100%.
But what happens when our fraction is less than 1? Let’s take a look.
Consider the fraction \(\frac{1}{4}\). Visually, this is what’s happening:
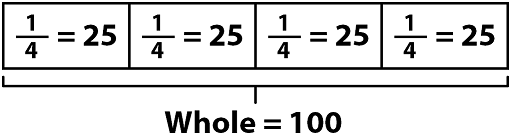
We can see in the diagram that \(\frac{1}{4}\) of the whole is \(\frac{25}{100}\). \(\frac{25}{100}\) means “25 per 100,” so it equals 25%.
Now let’s figure out how to convert this into a decimal.
We’re going to take our fraction \(\frac{1}{4}\), which is the same as saying 1 divided by 4.
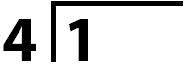
Dividing this way doesn’t look like it will work. But using our knowledge of place value, we can make it work:
First, rewrite the 1 as 1.0. Instead of 1, the dividend is now ten tenths.
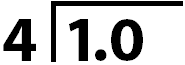
Second, 4 ones will go into ten-tenths two-tenths times.
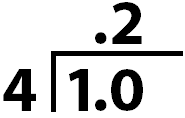
Third, \(4\times 0.2=0.8\).
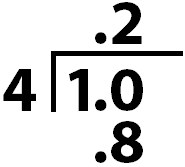
Fourth, \(1.0 -0.8 = 0.2\).
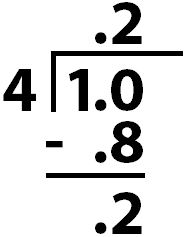
Fifth, we’re gonna rewrite the original dividend as 100-hundredths and bring the new 0 down.
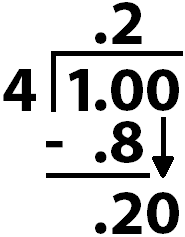
Sixth, 4 ones goes into 20-hundredths 5-hundredths times.
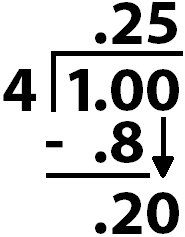
Seventh, we’re gonna multiply \(4\times 0.05=0.20\). Then we’ll subtract to get 0.
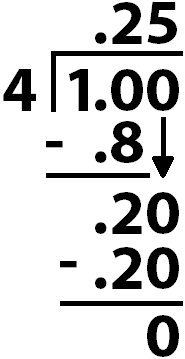
This means \(\frac{1}{4}=0.25\).
How to Convert Fraction to Percent
Let’s see this work with a non-unit fraction, like \(\frac{3}{16}\).
Here’s what the division looks like. The sequence of adding a decimal and dividing repeats as often as necessary until either the remainder is 0 or the decimal begins to repeat.
So, \(\frac{3}{16}=0.1875\) and \(0.1875=\frac{1,875}{10,000}=\frac{18.75}{100}\). Therefore, 0.1875 is the same as 18.75% because it’s 18.75 per, 100.
How about a repeating decimal? Everything is the same and the process can be stopped when it is clear that the decimal repeats. Here’s a quick example: \(\frac{1}{3}\).
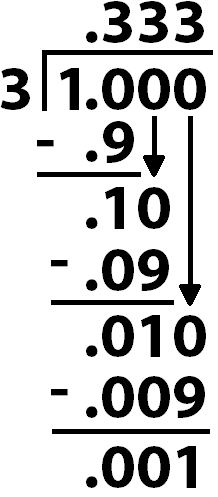
The process of subtracting 9 units from 10 units repeats, causing the decimal to repeat.
Lastly, consider a fraction that is greater than 1, such as \(\frac{5}{2}\).
Visually, here’s what we have:
We can see that the shaded quantity is \(\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{5}{2}\). Each \(\frac{1}{2}=50\), so we can say equivalently \(\frac{250}{100}\), which, as a decimal, is 2.5 (meaning \(2\frac{1}{2}\) wholes, which the diagram shows). We can also equivalently say 250 per 100, or 250%.
And the same works for the division as well:
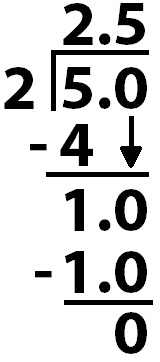
Thanks for watching and happy studying!
Frequently Asked Questions
Q
How do you change a fraction into a percent?
A
Converting a fraction to a percent can be accomplished in \(2\) quick steps.
Step 1: Divide the numerator by the denominator.
Step 2: Multiply this decimal by \(100\).
For example, \(\frac{2}{5}\) shows a numerator of \(2\), and a denominator of \(5\).
Step 1:
| \(5\phantom{.}\) | \(\phantom{.}2\) |
is the same as
| \(5\phantom{.}\) | \(\phantom{.}2\) | . | \(0\) | \(0\) |
, which equals \(0.4\) when using the process of long division.
Step 2: \(0.4\times100=40\). This means that the fraction \(\frac{2}{5}\) represents \(40\%\).
Q
How do I turn fractions into decimals?
A
Fractions can be converted into decimals by using long division. For example, the fraction \(\frac{4}{25}\) is expressing “\(4\) divided by \(25\)”. This can be set up as 25⟌4. Place a decimal and zeros after the \(4\) so that it becomes \(4.00\). Now we have 25⟌4.00. \(25\) does not go into \(4\), but it does go into \(40\), one time. From here, the standard rules of long division apply. The result will be \(0.16\). The important thing to remember is that the fraction bar represents division, so fractions can be calculated as decimals by dividing the numerator by the denominator.
Q
What is the meaning of a fraction bar?
A
A fraction represents “part” out of “whole”. The fraction bar separating the “part” and the “whole” represents division. For example, the fraction \(\frac{5}{9}\) represents \(5\) parts out of \(9\) parts, or “\(5\text{ divided by }9\)”. Another way to think about this, is that the fraction bar represents “per”. For example, \(\frac{40}{100}\) represents “\(40\text{ per }100\)”.
Q
What does percent mean?
A
Percent means “\(\text{per }100\)”. For example, \(96\%\) represents \(96\) per \(100\). This also represents the fraction \(\frac{96}{100}\). All percents can be expressed as a fraction because percents are always out of \(100\). Percents will sometimes be smaller than \(1\), and larger than \(100\). For example, the percent \(125\%\) represents \(\frac{125}{100}\), and the percent \(0.5\%\) represents \(\frac{0.5}{100}\).
Q
Why do you divide a fraction to turn it into a decimal?
A
Fractions represent a “part” out of a “whole”. The fraction bar separating the “part” and the “whole” represents division. This means that all fractions can be converted into decimals by dividing the numerator by the denominator.
For example, the fraction \(\frac{4}{5}\) represents \(4\) out of \(5\), or \(4\) divided by \(5\). This fraction can be converted into a decimal by dividing \(4\) by \(5\). 5⟌4 can be solved if a decimal point and zeros are added to the right of the \(4\). 5⟌4 becomes 5⟌4.00. \(5\) goes into \(40\) \(8\) times, and the rest of the process follows the standard rules of long division. The result is \(0.8\).
Fact Sheet
Practice Questions
What is \(\frac{42}{100}\) as a percent?
42%
4.2%
0.42%
420%
The correct answer is 42%. Percent means “per 100,” so to turn a fraction into a percent, convert the denominator to 100 and the numerator is your percentage.
What is \(\frac{16}{100}\) as a decimal?
16.00
0.016
0.16
1.6
The correct answer is 0.16. Since 16 is over 100, write the decimal so that 6 is in the hundredths place, which means 1 will be in the tenths place.
Which of the following is not a proper way to rewrite \(\frac{96}{1,000}\)?
0.096
96%
9.6%
0.09600
The correct answer is 96%. \(\frac{96}{1,000}\) as a decimal is 0.096 and adding zeroes to the end of a decimal number doesn’t change its value, so 0.09600 is equivalent to 0.096. \(\frac{96}{1,000}\) as a percentage is 9.6%. 96% as a fraction is \(\frac{96}{100}\).
What is \(\frac{7}{20}\) as a percent?
7%
20%
28%
35%
The correct answer is 35%. Percent means “per 100,” so to turn a fraction into a percent, convert the denominator to 100 and the numerator is your percentage. To convert \(\frac{7}{20}\) to have a denominator of 100, multiply both the numerator and the denominator by 5, which gives you \(\frac{35}{100}\). 35 is the numerator, so \(\frac{7}{20}=35%\).
What is \(\frac{23}{125}\) as a decimal?
0.23
1.25
1.86
0.184
The correct answer is 0.184. To convert a fraction to a decimal, first convert the fraction so it has a denominator of a multiple of 10. This can be done by multiplying \(\frac{23}{125}\) by \(\frac{8}{8}\). \(\frac{23}{125}\times\frac{8}{8}=\frac{184}{1,000}\), and since 184 is over 1,000, place the 4 in the thousandths place of the decimal, which puts 8 in the hundredths place, and 1 in the tenths place, 0.184.
Write the fraction \(\frac{4}{5}\) as a decimal.
0.8
0.6
0.5
0.4
The correct answer is 0.8. To convert a fraction to decimal, divide the numerator by the denominator. In this case, divide 4 by 5. Long division can be used for this:
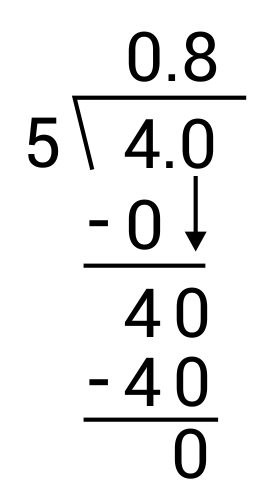
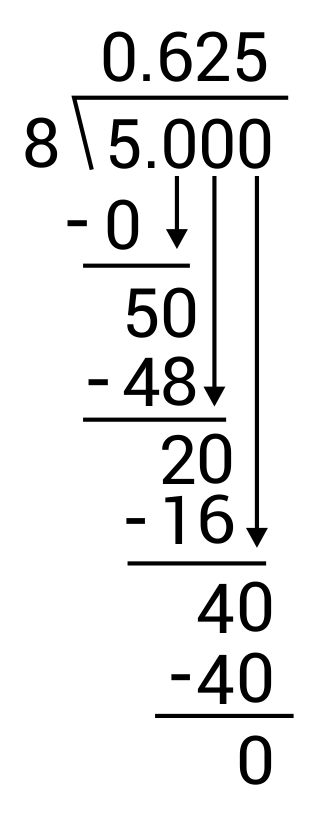
Write the fraction \(\frac{5}{8}\) as a decimal.
5.8
0.58
0.625
0.562
The correct answer is 0.625. To convert a fraction to decimal, divide the numerator by the denominator. In this case, divide 5 by 8. Long division can be used for this:
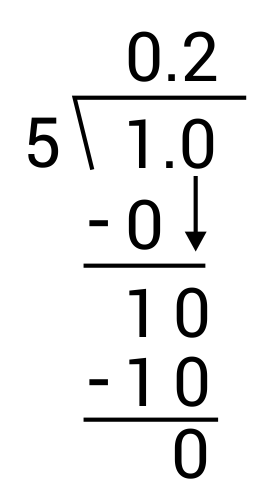
Write the fraction \(\frac{1}{5}\) as a decimal.
0.5
0.2
0.1
2.0
The correct answer is 0.2. To convert a fraction to decimal, divide the numerator by the denominator. In this case, divide 1 by 5. Long division can be used for this:
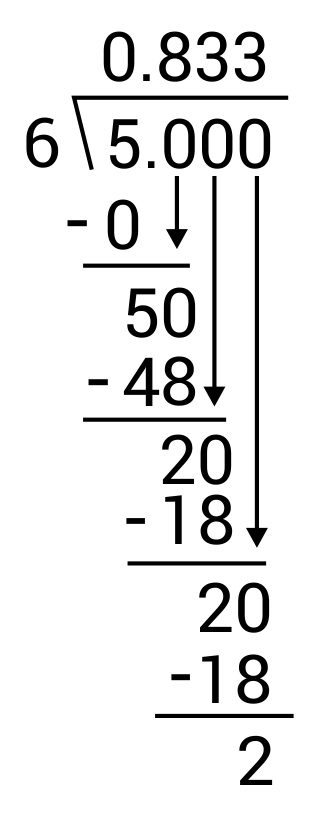
Write the fraction \(\frac{5}{6}\) as a decimal.
0.3222
0.8333…
0.8314
0.2333…
The correct answer is 0.8333. To convert a fraction to decimal, divide the numerator by the denominator. In this case, divide 5 by 6. Long division can be used for this:
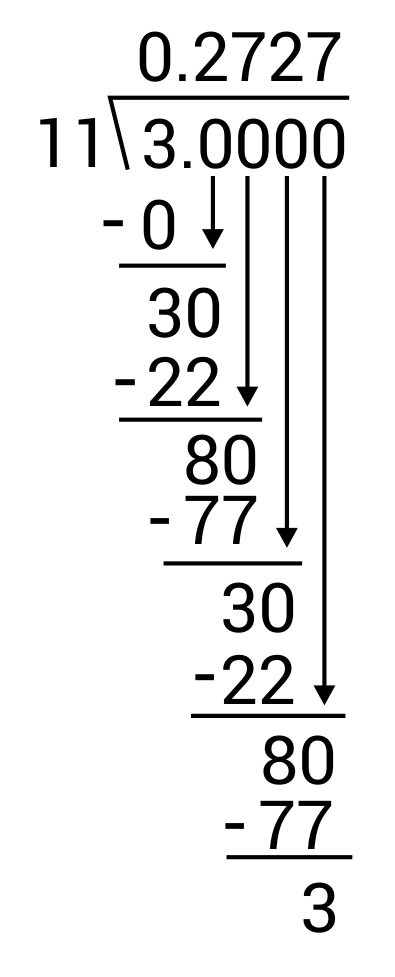
Write the fraction \(\frac{3}{11}\) as a decimal.
0.3111…
0.3131…
0.3535…
0.2727…
The correct answer is 0.2727…To convert a fraction to decimal, divide the numerator by the denominator. In this case, divide 3 by 11. Long division can be used for this:
