
Hey guys! Welcome to this video on adding and subtracting with exponents.
To start off, just so that we are all on the same page, I’m going to define exponents as well as a few other things so that moving forward, hopefully, there won’t be as much confusion.
So, I’ll start with the base (or variable base in this case). The base is the number that is being raised to the power of something, and that number it is being raised by is called the exponent. Now, what an exponent represents is how many times that base is being multiplied by itself. So, in this case, \(x\), our base, is being multiplied by itself twice (\(x \cdot x\)). The number out in front of the base or variable is called the coefficient. Hopefully, now, moving forward you will be able to better follow what I’m talking about as I reference these terms.
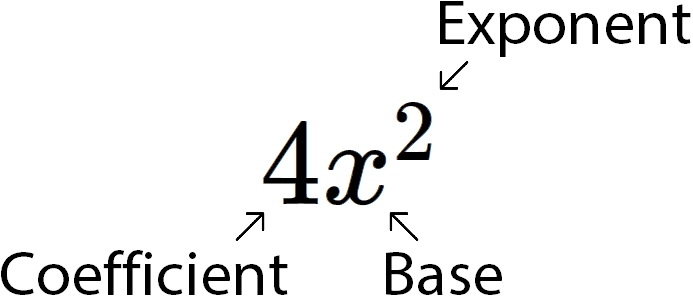
Now, let’s take a look at a problem.
Adding Exponents
Alright so in order for us to simplify this we have to look for two things. One, are our bases (or variables) the same; and two, are our exponents the same? Both things have to be true in order for us to add these two terms together. This same process of adding and subtracting with exponents is also called combining like terms, which may sound more familiar to you. Well, they are the same thing.
Okay, so looking back at our problem we can see that our bases are the same, and our exponents are the same. This means we have two like terms that can be combined together. So, to actually combine them here is what you do:
Add the coefficients together, and leave your base and exponent the same.
In this problem our coefficients are 5 and 9. 5 + 9 is equal to 14. So, leaving our base and exponent alone we get \(14x^3\).
Subtracting Exponents
Remember, to add or subtract numbers that have exponents you must first make sure that the base and exponent of the two terms you are trying to add or subtract are the same. If they are the same, then all you have to do is add together their coefficients and keep the base and exponent the same.
Let’s look at another example.
Alright, so in this example, some of the terms have different exponents. So, we need to identify all of our terms that can be combined together in order to simplify this expression. Starting with \(2x^2\), are there any other terms with an identical base and exponent? Yes, \(-x^2\). 5 is on it’s own, and \(-4x^3+7x^3\) share identical base and exponents.
Combining Like Terms
We know that to combine our like terms together, all we need to do is add together the coefficients of the corresponding like terms.
So, here is how we can do that.
Since, we are adding the coefficients of \(2x^2\) and \(-x^2\) together, and all other like terms, we can rewrite this expression to help us follow our work.
Now, the reason I brought my term with a 3 in the exponent to the front is because in the standard form of a polynomial equation, you always bring your term with the highest number in the exponent to the front (or to the left).
Now, when we add our coefficients together we get:
At this point, all of our like terms have been combined, and there is no further simplification that we can do. So, we are done.
I hope this video was helpful.
See you next time!
Adding and Subtracting Exponents Practice Questions
Identify the coefficient, base, and exponent in the following term: \(9x^3\)
In the term \(9x^3\), the 9 is a coefficient because it is the number in front of the variable, the x is the base because it is the variable that is raised to a power, and the 3 is an exponent, or the power that x is raised to. When terms have the same base and exponent they can be added or subtracted.
Simplify the following: \(3x^3-4+2x^2+5x^3+17\)
Terms that have the same base and exponent can be added or subtracted. These are often referred to as “like terms”. In the expression \(3x^3-4+2x^2+5x^3+17\), the “like terms” \(3x^3\) and \(5x^3\) can be combined in order to simplify. \(3x^3-4+2x^2+5x^3+17\) becomes \(8x^3+2x^2+13\).
Simplify the following: \(40x^2-3x^3+20-30x^3-2x^2\)
The terms with the same base and exponent can be combined. In this example, \(40x^2\) and \(-2x^2\) have the same base and exponent, and so do \(-3x^3\) and \(-30x^3\). When the “like terms” are combined, based on the sign that is in front of them (+ or -), the result is \(-33x^3+38x^2+20\).
A circular grassy courtyard has an area of \(8+5x^2\). There are two rectangular flower beds in the courtyard that have areas of
\(x^2\) and \(3x^2\). Write the expression for the area of the grassy courtyard not covered by flower beds.
The area of the rectangular flower beds can be subtracted from the area of the courtyard in order to determine the exposed grassy area. The area of the courtyard is \(8+5x^2\), so let’s subtract \(x^2\) and \(3x^2\) from this area. \((8+5x^2)-x^2-3x^2\) simplifies to \(x^2+8\) when the “like terms” \(5x^2\), \(-x^2\), and \(-3x^2\) are combined.
The side lengths of a triangle are \(x^3+10\), \(2x^2+5\), and \(2x^3+3x^2\). Express the perimeter of the triangle in simplest form.
The perimeter of the triangle is calculated by adding all three
side lengths. \((x^3+10)+(2x^2+5)+(2x^3+3x^2)\) can be calculated by combining “like terms” that have the same base and the same exponent. The “like terms” in this expression are \(x^3\) and \(2x^3\), \(2x^2\) and \(3x^2\), and 10 and 5. \((x^3+10)+(2x^2+5)+(2x^3+3x^2)\) becomes \(3x^3+5x^2+15\), which is the perimeter of the triangle.
