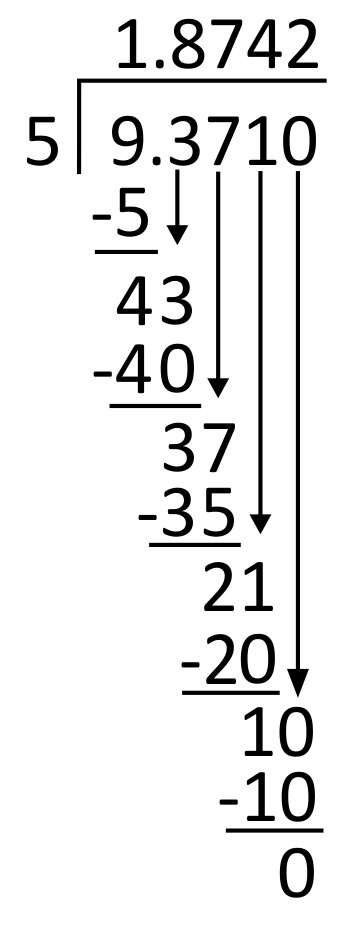Hi, and welcome to this video on dividing decimals by whole numbers.
Decimals represent part of a whole, so it may seem a little unusual to divide a part of something into different groups.
Dividing Decimals Examples
Example #1
If you had part of a slice of pizza because you had eaten the other part already, it would be a little weird to split the rest of that part with a couple of friends. But, if you had part of a whole pizza left, say four slices out of whole pizza made of 8, that’s not as weird to split with some friends.
Example #2
Another common way you will see division with decimals is involving money.
Consider this example: your grandma has $4.25 in coins and she wants to split the money evenly among her 5 grandkids.
Let’s go over the process of how to divide with decimals using this example.
When dividing a decimal by a whole number, you want to set up your division just like you would for regular long division, like this:
Then we will work the problem exactly like we would any other long division problem. The only difference being that we put a decimal point in our answer right above where it is placed in our problem, like this:
Now proceed with regular long division. You no longer need to think about that decimal.
So, 5 cannot go into four anytime so we’re gonna put a zero here and move on. Forty-two. Five goes into forty-two eight times. Eight times five is forty. So, we write a forty underneath and subtract. This gives us two then we bring the five down to get twenty-five. Five goes into twenty-five five times so we right a five up here. Subtract twenty-five and we’re left with zero.
This tells us that your grandma should give 85 cents to each of her grandchildren.
Let’s try a few more examples.
Example #3
\(8.275\div5 \)
First, set it up like a long division problem.
Then, place your decimal point in the appropriate place in your quotient.
And now, divide as you would typically with long division.
Five goes into eight one time so we’re gonna put a one up here. Five times one is five. Right down the five and subtract. This gives us three and we bring down our two. Five goes into thirty-two six times so we’re gonna write a six up here. Five times six is thirty. Write down the thirty and subtract. This gives us two and we’re gonna bring down the seven.
Five goes into twenty-seven five times so we’re gonna write a five up here. Five times five is twenty-five. Subtract twenty-five. Now, we have two we’re gonna bring down this five down. Five goes into twenty-five five times so we write a five up here. Five times five is twenty-five. Write twenty-five and subtract which gives us zero.
The final answer is 1.655.
Example #4
Here’s another one for us to try.
\(0.432\div 8\)
First, set up your long division problem.
Then, add your decimal point in the appropriate place.
And from there, divide as you would typically with a long division problem.
\(0.432\div 8\) is equal to 0.054.
Example #5
Let’s try one more together. This example will require a couple of extra steps that the last few didn’t.
\(1.973 \div 4 \)
First, set it up for long division.
Then, place the decimal point in the correct spot.
And divide out as you would normally.
In this problem, we encounter something we haven’t before, a remainder. If you recall when you first learned how to long divide, you were most likely taught to add a decimal and a zero and then keep dividing and adding zeroes until you no longer have a remainder. You can do this because 1.0 is the same as 1, which is also the same as 1.00. Adding a decimal point and zeroes after it doesn’t change the value of the original number because it just means adding zero parts to the whole.
With our example, you are going to do almost the same thing. However, instead of adding a decimal and a zero, you will just add a zero and continue dividing. This is because we already have a decimal point and you can’t have two.
After adding two zeroes, we finally get an answer without a remainder, 0.49325.
Example #6
I want to do one more example, but this time try it on your own first. I’ll give you the problem and then I want you to pause the video and find the answer yourself. Then, once you’ve got it, press play and see if it matches up with mine.
\(3.872 \div 5\)
Ready?
I’m going to start by setting up my long division problem.
Then I’ll add my decimal.
And finally, I’ll complete the long division process.
After adding an extra zero so I wasn’t left with a remainder, I got 0.7744.
I hope this review of dividing a decimal by a whole number was helpful. Thanks for watching and happy studying!
Dividing Decimals by Whole Number Practice Questions
Which of the following correctly sets up \(13.6\div4\) for long division?
| \(13.6\) | \(4\) |
| \(4\) | \(13.6\) |
| \(136\) | \(4\) |
| \(4\) | \(136\) |
The divisor, 4, is to the left of the long division symbol. The dividend, 13.6, is to its right. The decimal point remains in the division problem.
Divide 5.58 by 9.
| First, set up the problem for long division by writing the divisor, 9, to the left of the long division symbol and the dividend, 5.58, to its right. Then, write the decimal in the appropriate place in the quotient (above the long division symbol), aligned with the decimal in the dividend. |
| Since 9 can’t go into 5, place a zero in the quotient in the ones place. 0 times 9 equals 0, so write 0 below 5 to subtract. | ||||||||||||||||||||
| Subtract 5 minus 0 which is 5, and then bring down the next digit in the dividend, which is also 5. | ||||||||||||||||||||||||||||||
Subtract 55 minus 54, which equals 1, and then bring down the next digit in the dividend, which is 8.
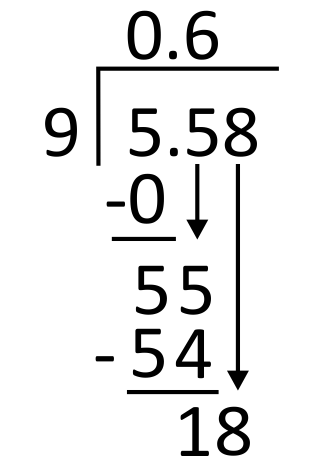
From here, divide 9 into 18. Since 9 goes into 18 two times, write 2 in the quotient in the hundredths place. 2 times 9 equals 18, so write 18 below 18 to subtract.
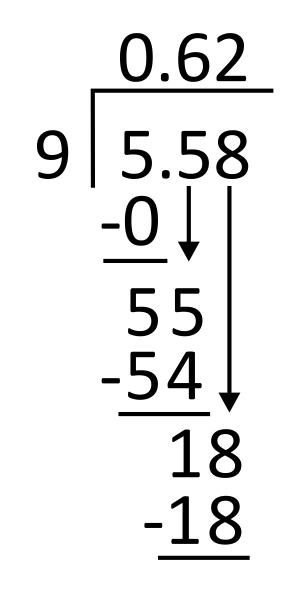
18 minus 18 is 0, so there is no remainder. The quotient is 0.62, so the correct answer is B.
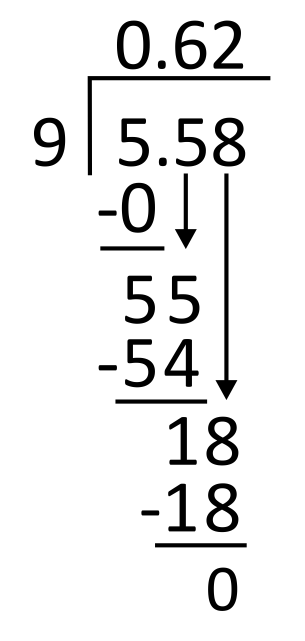
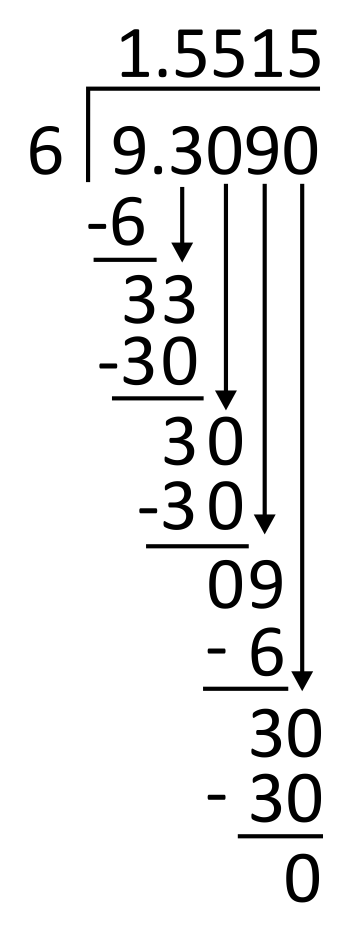
\(9.309\div6=\)
First, set up the problem for long division by writing the divisor, 6, to the left of the long division symbol and the dividend, 9.309, to its right. Then, write the decimal in the appropriate place in the quotient (above the long division symbol), aligned with the decimal in the dividend.

6 goes into 9 one time, so write 1 in the quotient in the ones place. 1 times 6 equals 6, so write 6 below 9 to subtract.
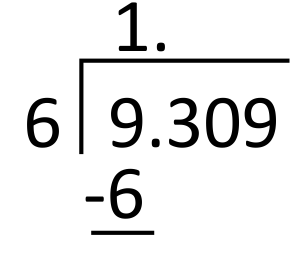
Subtract 9 minus 6 which is 3, and then bring down the next digit in the dividend, which is also 3.
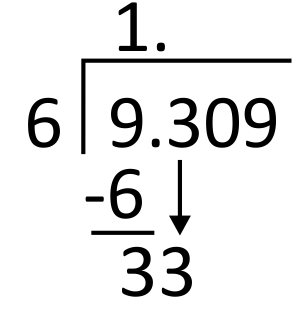
Next, divide 6 into 33. Since 6 goes into 33 five times, write 5 in the quotient in the tenths place. 6 times 5 equals 30, so write 30 below 33 to subtract.
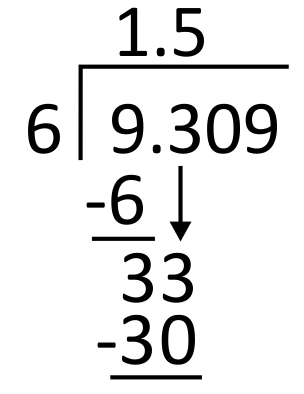
Subtract 33 minus 30, which equals 3, and then bring down the next digit in the dividend, which is 0.
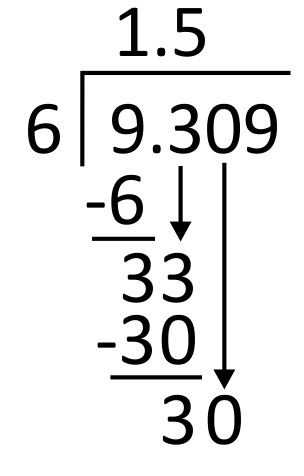
From here, divide 6 into 30. Since 6 goes into 30 five times, write 5 in the quotient in the hundredths place. 6 times 5 equals 30, so write 30 below 30 to subtract.
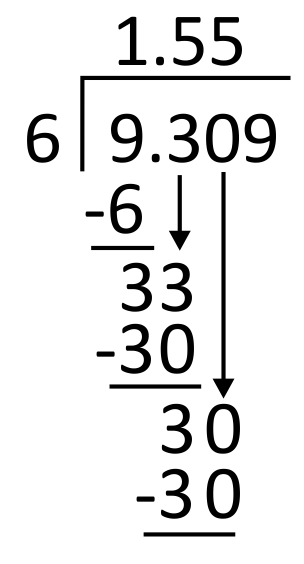
Subtract 30 minus 30, which equals 0. Then bring down the next digit in the dividend, which is 9.
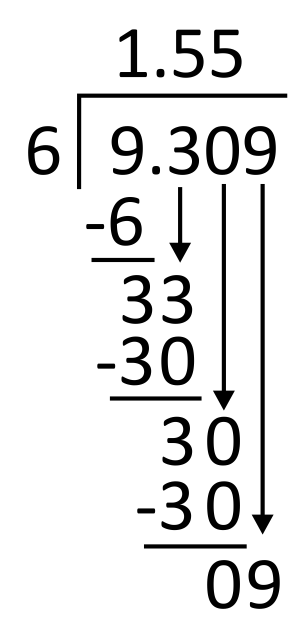
6 goes into 9 one time, so write 1 in the quotient in the thousandths place. 1 times 6 equals 6, so write 6 below the 9 to subtract.
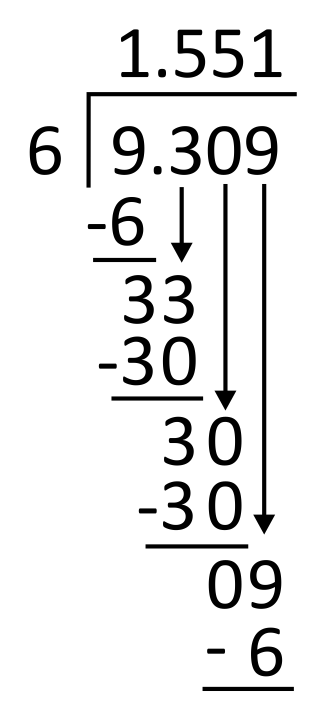
9 minus 6 equals 3, so there is a remainder. Since there are no remaining digits in the dividend to bring down, write a zero in the dividend’s ten-thousandths place. Bring down the zero.
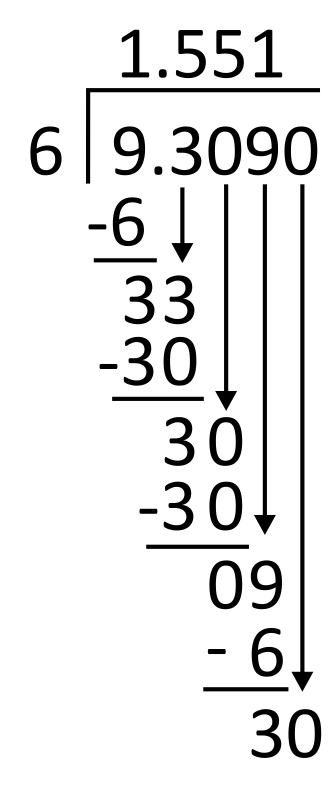
6 goes into 30 five times, so write 5 in the quotient in the ten-thousandths place. 6 times 5 equals 30, so write 30 below 30 to subtract.
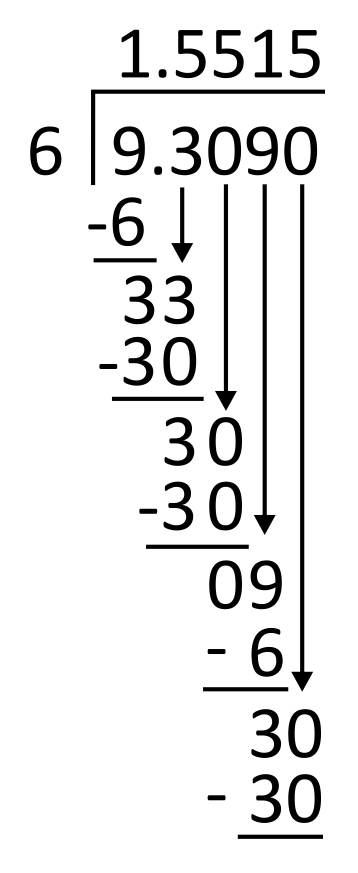
30 minus 30 is 0. The quotient is 1.5515, so the correct answer is D.
Kyle’s grandma left $49.12 on the kitchen table. She asked Kyle to split the money into four equal groups for Kyle and his three cousins. How much money should each grandchild receive?
First, set up the problem for long division by writing the divisor, 4, to the left of the long division symbol and the dividend, 49.12, to its right. Then, write the decimal in the appropriate place in the quotient (above the long division symbol), aligned with the decimal in the dividend.

4 goes into 4 one time, so write 1 in the quotient in the tens place. 1 times 4 equals 4, so write 4 below 4 to subtract.
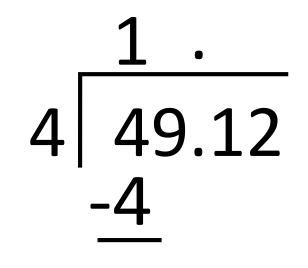
Subtract 4 minus 4 which is 0, and then bring down the next digit in the dividend, which is 9.
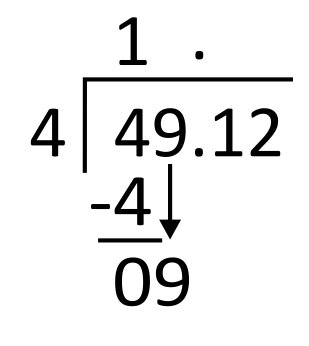
Next, divide 4 into 9. Since 4 goes into 9 two times, write 2 in the quotient in the ones place. 2 times 4 equals 8, so write 8 below 9 to subtract.
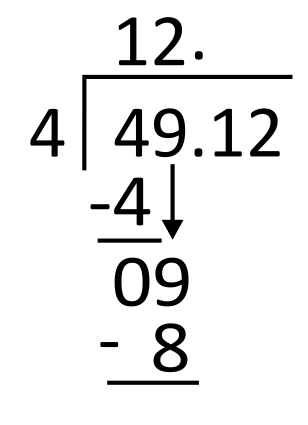
Subtract 9 minus 8, which equals 1, and then bring down the next digit in the dividend, which is also 1.
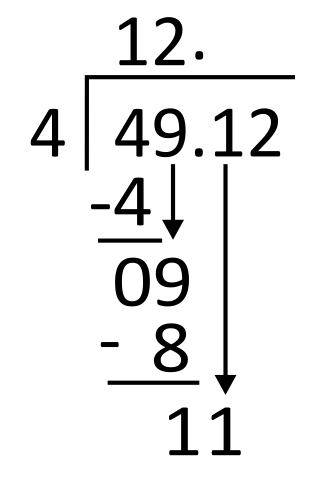
From here, divide 4 into 11. Since 4 goes into 11 two times, write 2 in the quotient in the tenths place. 2 times 4 equals 8, so write 8 below 11 to subtract.
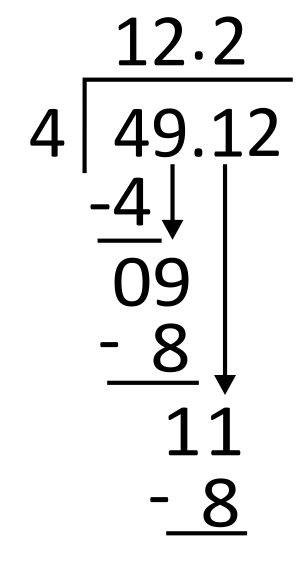
Subtract 11 minus 8, which equals 3. Then bring down the next digit in the dividend, which is 2.
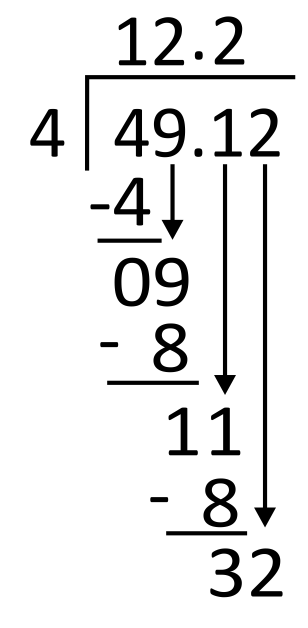
Next, divide 4 into 32. Since 4 goes into 32 eight times, write 8 in the quotient in the hundredths place. 8 times 4 equals 32, so write 32 below 32 to subtract.
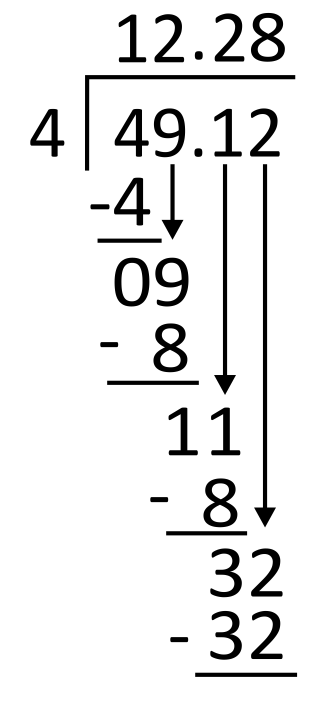
32 minus 32 is 0, so there is no remainder. The quotient is 12.28, so each grandchild should receive $12.28. The correct answer is A.
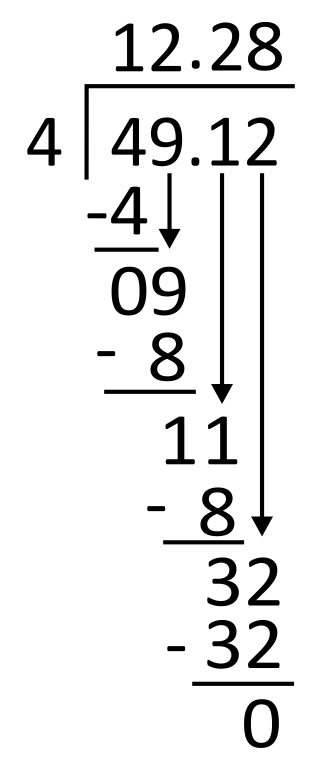
James is working on a carpentry project and needs to split a 9.371-inch plank into 5 equal parts. How long should each part be?
First, set up the problem for long division by writing the divisor, 5, to the left of the long division symbol and the dividend, 9.371, to its right. Then, write the decimal in the appropriate place in the quotient (above the long division symbol), aligned with the decimal in the dividend.

5 goes into 9 one time, so write 1 in the quotient in the ones place. 1 times 5 equals 5, so write 5 below 9 to subtract.
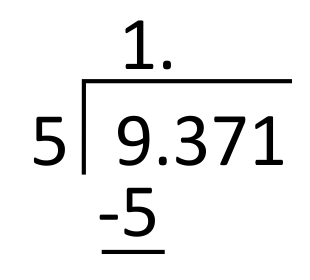
Subtract 9 minus 5 which is 4, and then bring down the next digit in the dividend, which is 3.
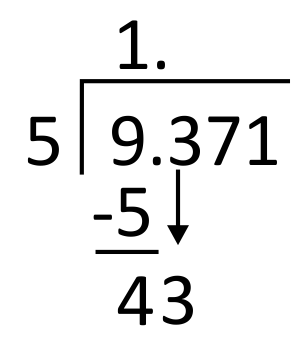
Next, divide 5 into 43. Since 5 goes into 43 eight times, write 8 in the quotient in the tenths place. 8 times 5 equals 40, so write 40 below 43 to subtract.
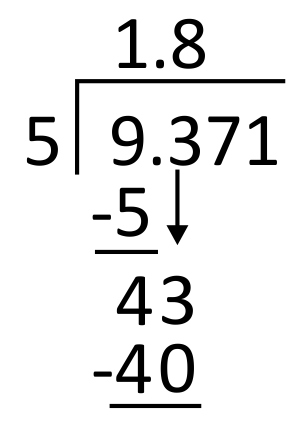
Subtract 43 minus 40, which equals 3, and then bring down the next digit in the dividend, which is 7.
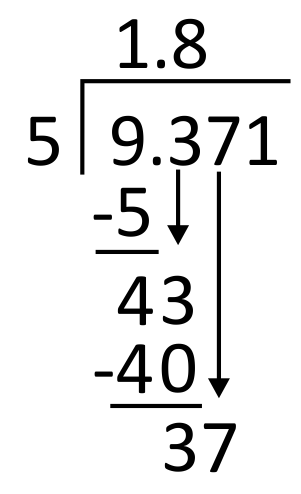
From here, divide 5 into 37. Since 5 goes into 37 seven times, write 7 in the quotient in the hundredths place. 7 times 5 equals 35, so write 35 below 37 to subtract.
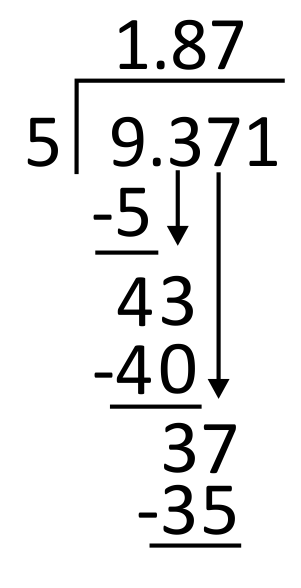
Subtract 37 minus 35, which equals 2. Then bring down the next digit in the dividend, which is 1.
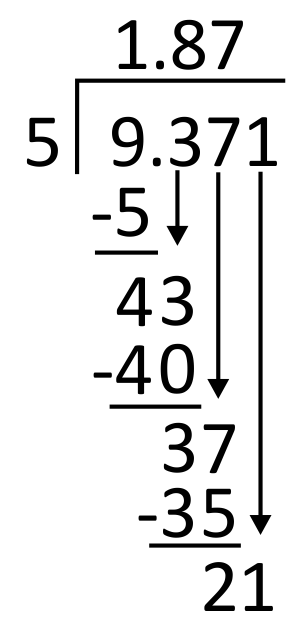
Next, divide 5 into 21. Since 5 goes into 21 four times, write 4 in the quotient in the thousandths place. 4 times 5 equals 20, so write 20 below 21 to subtract.
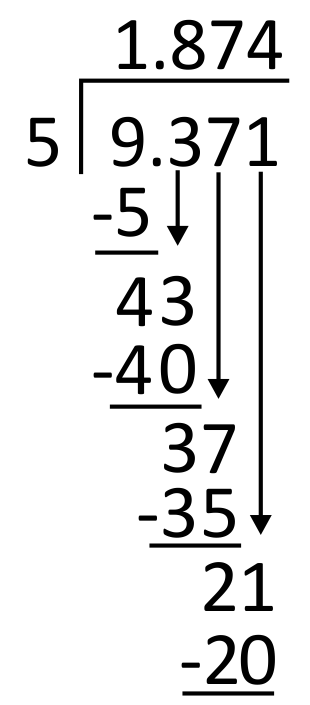
21 minus 20 equals 1, so there is a remainder. Since there are no remaining digits in the dividend to bring down, write a zero in the dividend’s ten-thousandths place. Bring down the zero.
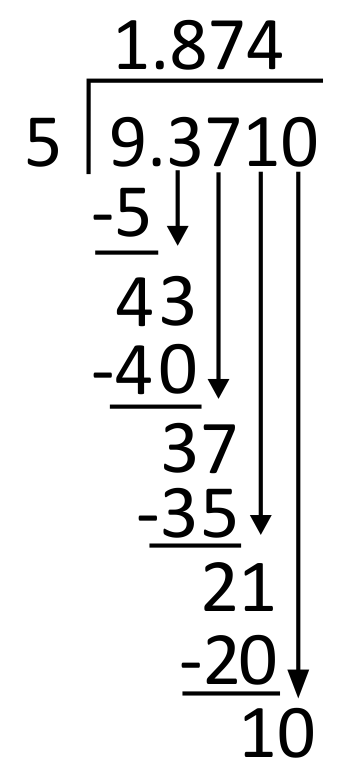
5 goes into 10 two times, so write 2 in the quotient in the ten-thousandths place. 2 times 5 equals 10, so write 10 below 10 to subtract.
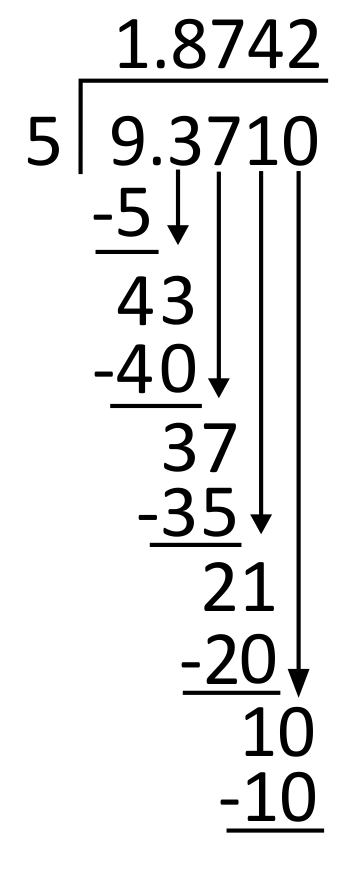
10 minus 10 is 0. The quotient is 1.8742, so each piece should be 1.8742 inches long. The correct answer is C.