Multiples
Hello and welcome to this video about multiples! In this video, we’ll take a look at
- What is a multiple in math?
- Common multiples
- Least common multiples
Multiple Examples
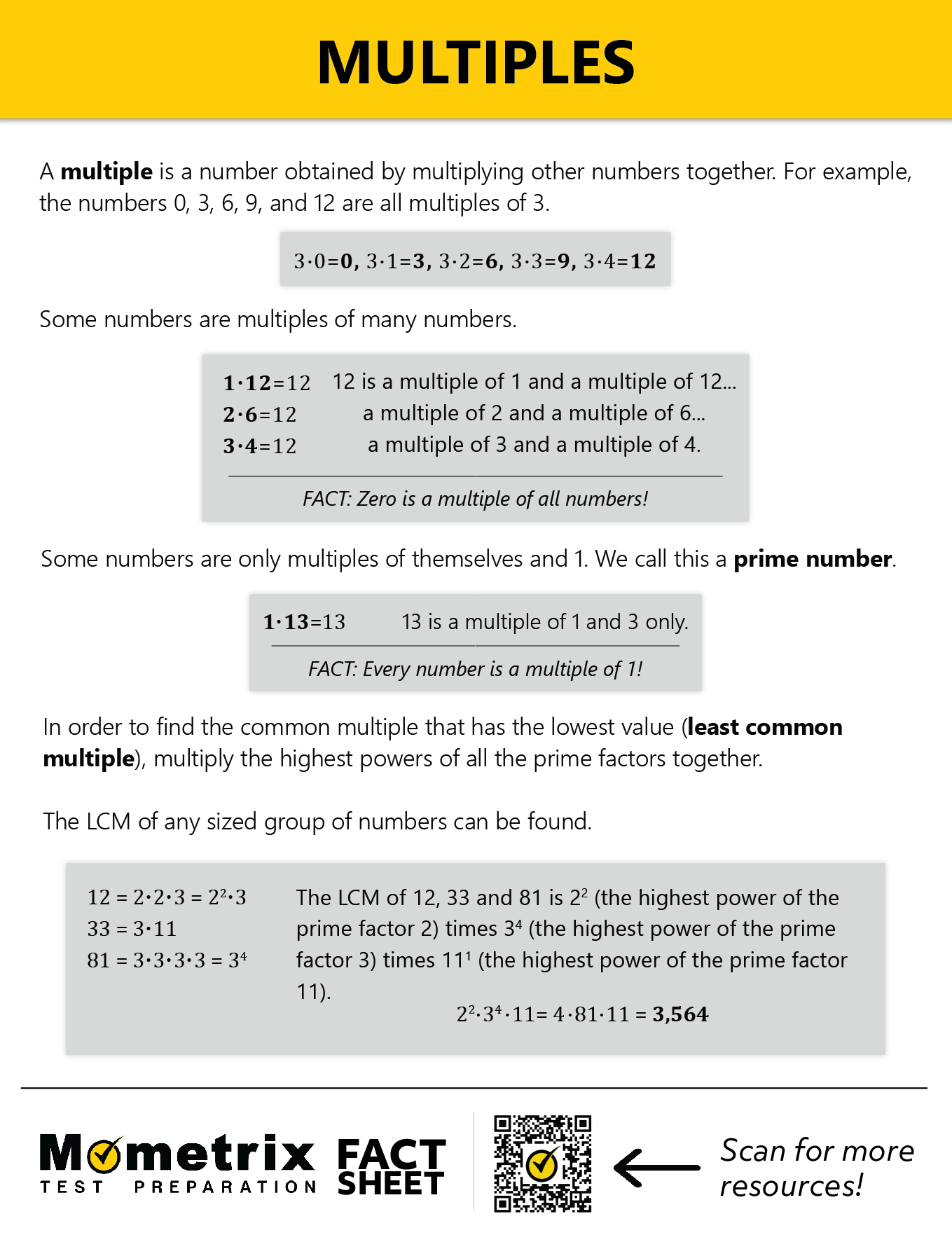
So first thing’s first—what is a multiple? Well, a multiple is any number obtained by multiplying other numbers together. Multiples are most commonly discussed in the context of integers. Let’s begin with a simple multiplication table:
| \(3 \times 0=0\) | |
| \(3 \times 1=3\) | |
| \(3 \times 2=6\) | |
| \(3 \times 3=9\) | |
| \(3 \times 4=12\) |
The numbers 0, 3, 6, 9, and 12 are all multiples of 3. In order to obtain them, 3 is being multiplied by another number. Any number has an infinite amount of multiples.
Some numbers are multiples of many different numbers. Take 12 for example:
| \(1 \times 12=12\) | |
| \(2 \times 6=12\) | |
| \(3 \times 4=12\) |
12 is a multiple of 1, 2, 3, 4, 6, and 12. These numbers can be multiplied by other numbers to obtain 12. As a reminder, 1, 2, 3, 4, 6, and 12 would be called factors of 12.
Other numbers are only multiples of 2 numbers, for example, 7:
| \(1 \times 7=7\) |
7 is a multiple of 1, and 7 only (1 and 7 are the only factors of 7). Because of this, 7 is an example of a prime number.
Now that we know what multiples are, here are a couple of truths to remember about them:
- First, 0 is a multiple of all numbers. For any number \(a\): \(a\times 0=0\)
- and secondly, every number is a multiple of 1 and itself. For any number \(a\), \(a \times 1=a\)
When comparing numbers, sometimes they are compared by their common multiples, or multiples that the numbers have in common.
Here are some common multiples of 4 and 10:
| \(4 \times 5=20\) | \(10 \times 2=20\) | |
| \(4 \times 10=40\) | \(10 \times 4=40\) | |
| \(4 \times 15=60\) | \(10 \times 6=60\) | |
| \(4 \times 20=80\) | \(10 \times 8=90\) | |
| \(4 \times 25=100\) | \(10 \times 10=100\) |
20, 40, 60, 80, and 100 are all multiples of both 4 and 10.
We can find common multiples of more than two numbers as well. Let’s look at 3, 5, and 9:
| \(3 \times 15=45\) | \(5 \times 9=45\) | \(9 \times 5=45\) | |
| \(3 \times 30=90\) | \(5 \times 18=90\) | \(9 \times 10=90\) | |
| \(3 \times 45=135\) | \(5 \times 27=135\) | \(9 \times 15=135\) |
45, 90, and 135 are all common multiples of 3, 5, and 9.
Sometimes, we need to determine the least common multiple (LCM) of a set of numbers, in other words, the common multiple that has the lowest value.
This can be done in one of two ways: listing the common multiples and factoring. Before, we listed the common multiples of two different sets of numbers. The LCM of 4 and 10 is 20, while the LCM of 3, 5, and 9 is 45.
Now let’s find the LCM of 4 and 10 by factoring. Remember, factors are numbers that are multiplied together to form a multiple. The LCM of two numbers is the product of the highest power of all prime factor of both numbers. Let’s break that down a bit:
| \(4=2 \times 2\) | \(10=5 \times 2\) |
| The prime factor of 4 is 2. | The prime factors of 10 are 5 and 2. |
|
Now let’s find the LCM of 24, 144, and 48 by factoring:
| \(24=2^3 \times 3\) |
| The prime factors of 24 are 2 and 3. |
| \(144=12 \times 12=2^4 \times 3^2\) |
| The prime factors of 144 are 2 and 3. |
| \(48=16 \times 3=2^4 \times 3\) |
| The prime factors of 48 are 2 and 3. |
The unique factors here are 2 and 3. The highest power of 2 is 4 and the highest power of 3 is 2. The LCM equals \(24 \times 32=144\). Since 144 is a multiple of both 24 and 48, it is also automatically the LCM of all three numbers.
I hope that this video has increased your understanding of multiples and how they work with numbers!
See you next time!
Frequently Asked Questions
Q
What are multiples and factors?
A
Factors and multiples are very closely related. Factors are the numbers we can multiply together in order to get another number. The number that is created by multiplying these factors is called a multiple. Multiples can be found by multiplying factors, or simply by skip counting. For example, the multiples of \(5\) can be found by skip counting by \(5\)s: \(5,10,15\)…
Q
What is the difference between a factor and a multiple?
A
Factors are the numbers that are multiplied in order to create a multiple. Multiples are the numbers created by multiplying two factors. Multiples are unlimited, and can be found by simply skip counting. For example, the multiples of \(30\) are \(30,60,90\)… and so on. However, the factors of \(30\) are limited. The factors of \(30\) are the numbers that multiply to \(30\), such as \(1\times30\), \(2\times15\), and \(5\times6\).
Q
What is a multiple in math?
A
A multiple can be found by skip counting, but it is also the result of multiplying a number by an integer. This integer can be positive or negative. For example, \(-6\) is a multiple of \(3\) because \(3\times-2=-6\).
Q
How do you calculate multiples?
A
Multiples can be found simply by skip counting. For example, the multiples of \(7\) can be found by skip counting by \(7\)s: \(7,14,21,28,35\)… Multiples can also be calculated by multiplying two factors. For example, \(4\) and \(5\) can be multiplied to create the product \(20\), which makes \(20\) a multiple of both \(4\) and \(5\).
Q
Why are factors and multiples important?
A
Factors and multiples are important in the field of math in many ways. For example, factors and multiples are used when looking for patterns in numbers, simplifying fractions, or when determining the greatest common factor. For example, when simplifying the fraction \(\frac{8}{10}\), we see that both \(8\) and \(10\) share a common factor of \(2\), so both numbers can be divided by \(2\) in order to simplify the fraction. \(\frac{8}{10}\) becomes \(\frac{4}{5}\).
Q
What is the definition of a factor in math?
A
Factors are the numbers we can multiply together in order to get another number. For example, the factors of \(20\) are \(1,2,4,5\) and \(20\) because these numbers can be multiplied together to get \(20\). \(1\times20=20\), \(2\times10=20\), and \(4\times5=20\). Technically, factors can be negative as well, but in general, when you are listing the factors of a number, you only need to list the positive factors.
Q
What does it mean to be a multiple?
A
In order for a number to be considered a multiple, it needs to be the result of multiplying a number and an integer. An integer is simply a whole number that is not a fraction. For example, \(36\) is a multiple of \(9\) because we can multiply \(9\) by \(4\) and the product is \(36\). It can be helpful to think about multiples as the result of skip counting. For example, \(36\) is a multiple of \(9\) because we can skip count by \(9\)s and reach \(36\): \(9,18,27,36\).
What is a Multiple? PDF
Multiple Practice Questions
Which list shows values that are all multiples of 4?
The correct answer is 0, 4, 8, 12, 16.
Multiples of 4 can be found by multiplying 4 by another number. For example, \(4×3=12\), so 12 is a multiple of 4. \(4×2=8\), so 8 is a multiple of 4. A number like 18 is not a multiple of 4 because we cannot multiply 4 by another number and get 18 as the product.
Determine the LCM of 42 and 126.
The correct answer is 126.
\(42=2×3×7\)
\(126=2×3×3×7\)
The highest power of 2 is one.
The highest power of 3 is two.
The highest power of 7 is one.
When we multiply these factors using the highest power, we have \(2×3^2×7\), which simplifies to 126. This means that 126 is the LCM of 42 and 126.
What is the LCM of 3, 5 and 8?
The correct answer is 120.
Let’s write the prime factorization for 3, 5 and 8.
\(3=3\)
\(5=5\)
\(8=2^3\)
Now multiply the unique factors using the highest power.
\(2^3×3×5=120\)
This means that 120 is the LCM of 3, 5 and 8.
Zoe has a watering schedule for her two plants. She waters her cacti every 10 days and her lilies every 3 days. If she waters both plants today, the first day of the month, what day will it be when she waters both plants again on the same day?
The correct answer is 30th day.
The cacti are watered every 10th day and the lilies are watered every 3rd day. We can list the multiples of 10 and 3, and then look for the next day they both have in common.
10: 10, 20, 30, 40, 50
3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36
The next day that both plants will be watered is on the 30th day of the month. In other words, the LCM of 10 and 3 is 30.
Marcus swims every 3rd day and hikes every other day. If today is January 5 and he swam and hiked, when will he swim and hike on the same day again?
The correct answer is January 11.
Marcus swims every 3 days and hikes every 2 days so we can solve this problem by determining the LCM of 3 and 2. The LCM of 3 and 2 is 6, and 6 days from January 5 is January 11.
