Prime Factorization

Hey, guys! Welcome to this video on prime numbers and prime factorization.

A prime number is any number that can only be divided by either one or by itself.

This means that a prime number will always be odd, except for the number 2. The only reason that is the case is because two is only the second numerical whole number. So, the only options for it to be divided by (without getting a fraction) are 1 and 2. Numerically, the first several prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29. There are an infinite amount of prime numbers.

Let’s practice identifying prime numbers.

Is 9 a prime number? Well, it can be divided by 1 and by itself, but are there any other numbers it can be divided by? Yes. 3 goes into 9 three times.

What about 31? Is it a prime number? Yes. There is not another number other than 1 and itself that it can be divided by without getting a fraction!

Now, let’s take a look at prime factorization.

If you recall, factors are any numbers that you multiply together to get another number.

Well, prime factorization uses this same concept, except you are only looking for the prime numbers that you are multiplying together to get the original number.

What are the prime factors of 24?

The easiest way to start is by starting with the smallest prime numbers, which will always be 2, so let’s see if that works.

So, 2 divides evenly into 24 to get 12, but 12 is not a prime number, so we must go even further.

Let’s try 3.

3 worked as well, but our result still isn’t a prime number. When we divide 3 into 12 we get 4, so we must go even further.

Let’s try 2 again.

Great, so it worked! We’ve gone the furthest we can go.

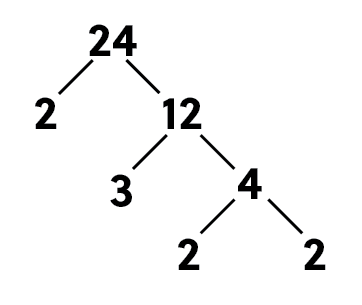
So, once we’ve factored everything out, to write this out to show our prime factorization, we’re only concerned with our prime numbers here.

So what we have is \(24=2\times 3\times 2\times 2\). We can even write this as \(24=2^{3}\times 3\).

Let’s take a look at another one.

What is the prime factorization of 72?

Let’s start with 2.

2 goes into 72, 36 times; but 36 is not a prime number. So, we must go further.

Let’s try 3 now. 3 goes into 36, 12 times; but 12 is not a prime number.

Let’s try 3 again. 3 goes into 12, 4 times; but, yet again, 4 is not a prime number. So, We need to go further.

2 goes into 4, 2 times.

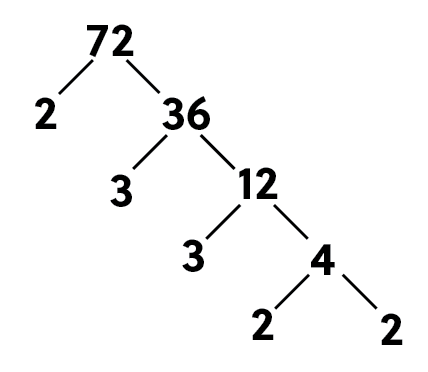
So now, we have our answer!

\(72=2^{3}\times 3^{2}\)

Spend some time practicing prime factorization on your own. Remember, when you write out your answer, you are only concerned about the prime numbers that multiply together to get the original number.

I hope this video has been helpful. For further help be sure to check out more of our videos by subscribing to our channel below.

See you next time!

Prime Factorization Practice Questions