Hello and welcome to this video about proportions! In this video, we will explore what proportions are, what it means for quantities to be proportional, and mathematical and authentic applications of proportions.
Before we get into proportions, we need to quickly review ratios. Recall that a ratio shows the relative sizes of two or more quantities. For example, in the alphabet, the ratio of vowels to consonants is \(\frac{5}{21}\). In a standard deck of cards, the ratio of face cards to non-face cards is \(\frac{12}{52}\). In all circles, the ratio of the circumference to the diameter is pi.
There are many ways to represent ratios. Here, we’ll mainly be working with the fractional representation. Ratios are not exactly fractions, but they can behave just like them.
Now onto proportions. A proportion states that two ratios are equal. If I want to cook 1 cup of white rice, I would combine it with 2 cups of water. In other words, for every cup of rice, I need 2 cups of water. So the ratio of rice to water is \(\frac{1}{2}\). If I wanted to double the recipe, I would need 2 cups of rice and 4 cups of water. So 1 over 2 is equal to 2 over 4.
These recipes are proportional because this is a true statement. In other words, their fractional forms are equivalent. On the other hand, the recipe for brown rice calls for every one cup of rice, three cups of water. The recipes for white rice and brown rice are not proportional, because \(\frac{1}{2} \neq \frac{1}{3}\).
Let’s look at using proportions to find quantities. In a standard deck of cards, the ratio of face cards to non-face cards is \(\frac{12}{52}\). Dealers in casinos often use 8 decks for blackjack. How many face cards would they use?
In 8 decks, the ratio of face cards to non-face cards is still \(\frac{12}{52}\), so these quantities of cards are proportional. There would be 96 face cards.
Let’s look at another example. The length of a rectangle is 4 units and its width is 3 units. The length of a second rectangle is 8 units and its width is 3 units. Are the rectangles proportional? Let’s write this out:
Since the ratios of length to the width are not equivalent, the rectangles are not proportional.
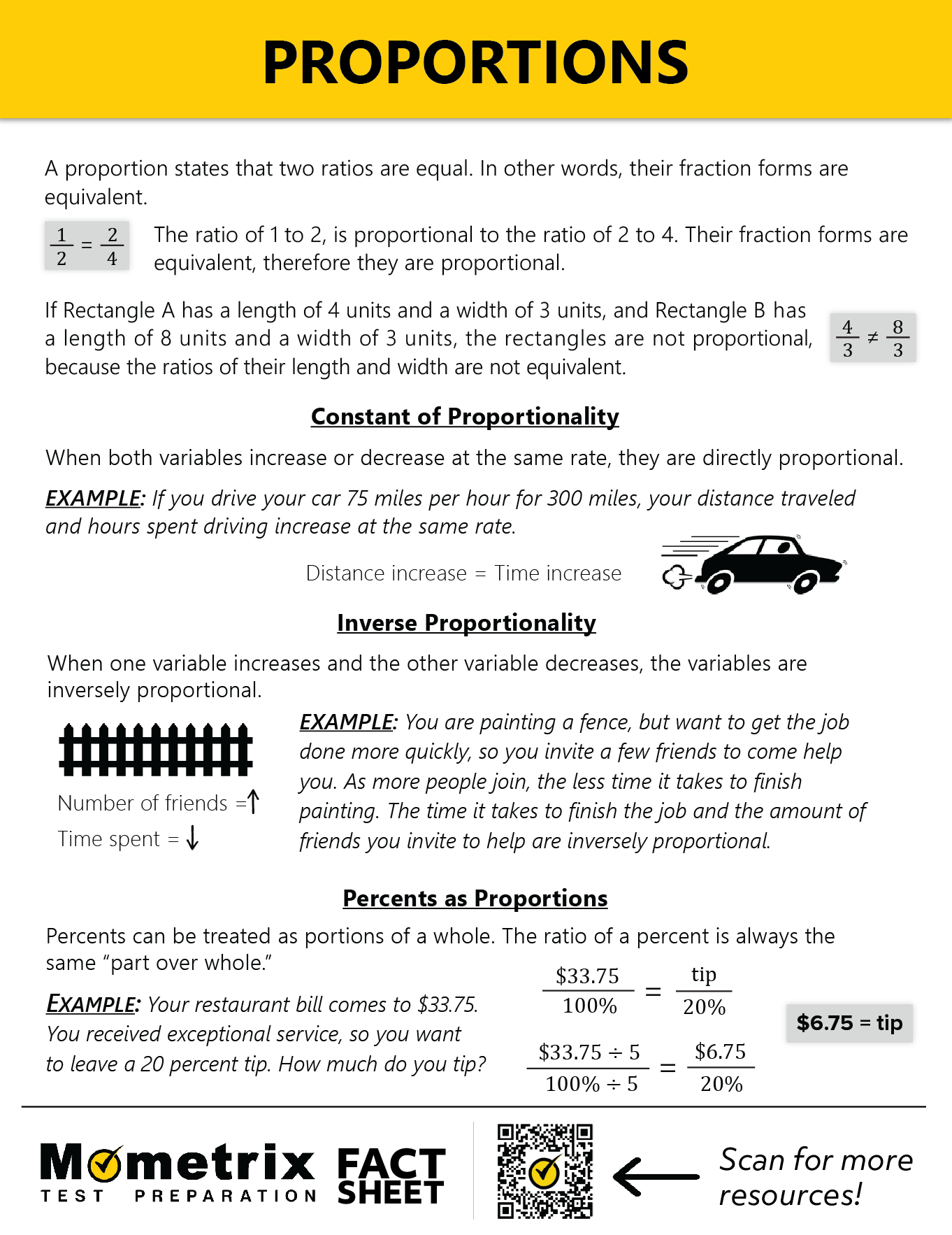
Now, suppose you’re driving a car at 75 miles per hour heading to a destination that’s 300 miles away. That is, for every hour that passes, you drive 75 miles. In this case, distance is directly proportional to hours because as hours increase, distance also increases and the rate of increase does not change.
This table shows an increase of 75 miles for every 1 hour, and the graph shows a straight line intersecting the origin:
| Hour \(h\) | Distance \(d\) from start |
|---|---|
| 0 | 0 |
| 1 | 75 |
| 2 | 150 |
| 3 | 225 |
| 4 | 300 |
The equation is of the form \(y=kx\), where \(k\) is the constant of proportionality. Here, the constant of proportionality is 75. Every hour amount is multiplied by 75 to calculate distance.
Now, let’s consider the same journey, but with a different relationship. You travel the same 300 miles, but instead of traveling at 75 miles per hour, you travel at 60 miles per hour. How much longer does the trip take at the slower speed? From the previous example, we know that \(y = 75 \times 4 = 300\) Now you are driving slower, so you have y equals \(60 \times x\) (which represents the number of hours traveled) \(=300\). So to solve for \(x\), you divide by \(60\) on both sides and get \(x=5\).
\(x=\)\(\frac{300}{60}\)
\(x = 5\)
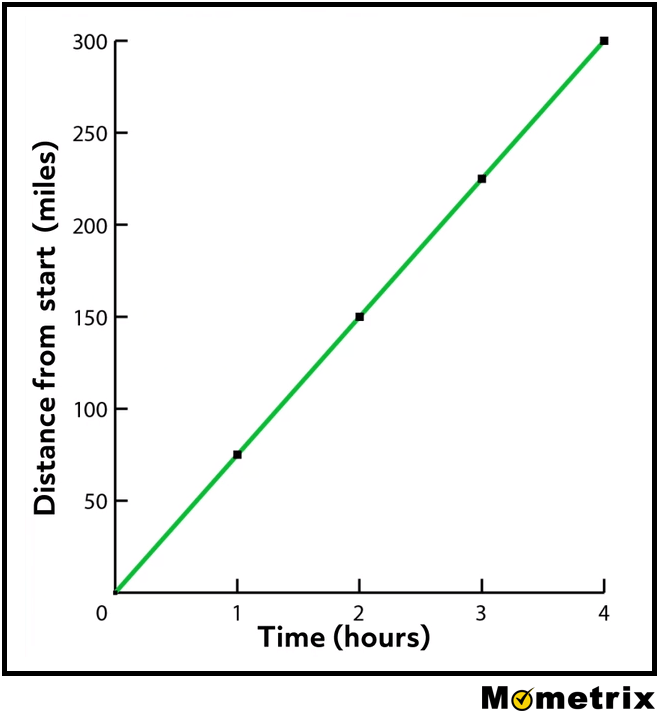
Here, distance is inversely proportional to time because, as time increases, distance to the destination decreases. You get closer every hour. The distance doesn’t change, so the constant of proportionality is 300. What does change is the speed.
| Hour \(h\) | Distance \(d\) from start |
|---|---|
| 0 | 300 |
| 1 | 240 |
| 2 | 180 |
| 3 | 120 |
| 4 | 60 |
| 5 | 0 |
The graph above shows all possible speed/time combinations to drive the 300-mile distance. If you drive 300 mph, it would take you 1 hour, whereas if you drive 1 mph, it would take you 300 hours!
Equations showing inverse proportionality have the form \(y=\frac{k}{x}\), where \(k\) is, again, the constant of proportionality. Here, the distance 300 could be divided by the number of hours to calculate the speed or it could be divided by the speed to calculate the number of hours.
Suppose you drove to the same place again and it took you 3.5 hours. How fast did you drive? Well, you’ve got \(y\), which is your speed, is equal to \(k\) (your constant of proportionality), which is 300. Divide this by the total number of hours, 3.5, and that gives you that your speed is roughly 86 miles per hour.
\(y=\frac{300}{k}\)
\(y=\frac{300}{3.5}\)
\(y \approx 86\) mph
Percentages as Proportions
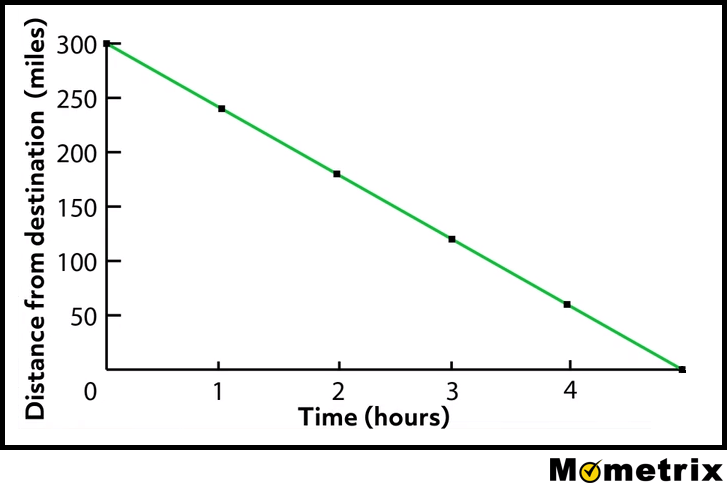
Now that we’ve covered proportions, let’s talk about percentages. When we deal with percents, they can be treated like proportions. The word percent literally means “per 100,” so knowing that, we can figure out any relationship we need to. The key to percents is figuring out “the whole” and “the part.” Simply put, the whole is the quantity represented by 100% and the part is the piece of the whole represented by some other percent.
Generally, proportions with percents show the whole amount over 100 is equal to the partial amount over the partial percent:
Your restaurant bill comes to $33.75. You received exceptional service, so you want to leave a 20% tip. How much do you tip? Using a bar model can come in handy when visualizing these problems. For instance, 33.75 over 100 is equal to whatever your tip is going to be over 20. So if you look we can do 33.75 over 100, divided by 5 over 5, and that gives you 6.75 over 20.
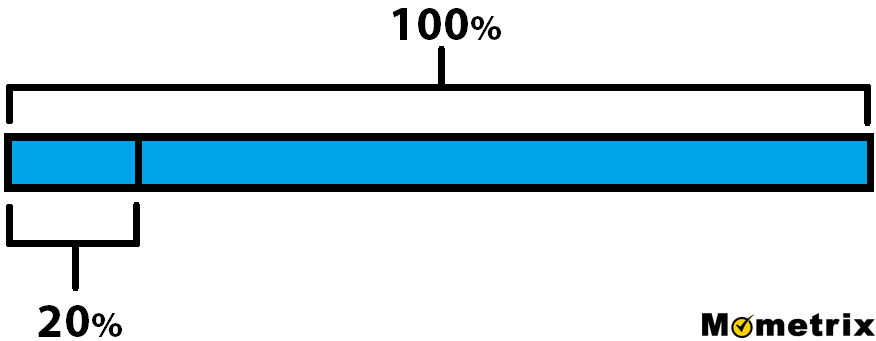
\(\frac{33.75}{100}=\frac{ \text{tip}}{20}\)
\(\frac{33.75\div 5}{100\div 5}=\frac{6.75}{20}\)
Since the total amount is proportional to the tip amount, we can simply divide the total amount by 5 to arrive at the tip amount. Division by 5 also makes sense because 20 is one-fifth of 100.
Suppose you went back to the restaurant, had a bill of $26.34, but decided to leave the typical 15% tip. How much did you leave? The bar model still helps us visualize:
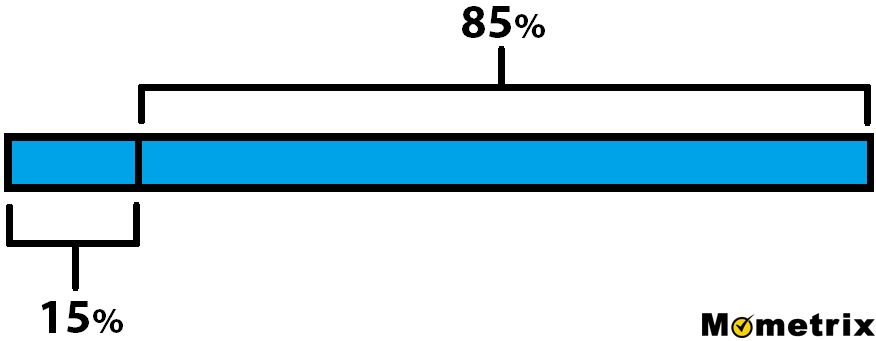
\(\frac{26.34}{100}=\frac{\text{tip}}{15}\)
So we have 26.34 over 100 is equal to our tip amount over 15. This time it’s not as easy as dividing by 5, since 15 doesn’t go evenly into 100.
Here’s a different way of using equations to think about it: If 26.34 is equal to 100 percent, then 0.2634 is equal to 1 percent. From there we’re going to multiply both sides by 15 and you get 3.951 is equal to 15 percent. If 26.34 = 100%, then .2634 = 1% by dividing both sides by 100. And 3.951 = 15% by multiplying both sides by 15. Now we know you left about $3.95.
You visit a store that’s having a 25%-off sale. You pick out some clothes and your total comes to $140.67. How much would full price have been, and how much did you save?
With a 25 percent discount, that means you paid 75 percent of the full price. So you have your original price over 100, which is equal to 140.67 over 75. 140.67 is equal to 75 percent, so if you divided both sides by 3, you get 46.89 is equal to 25 percent. And then if you multiply both sides by 4, you get 187.56 equals 100 percent.
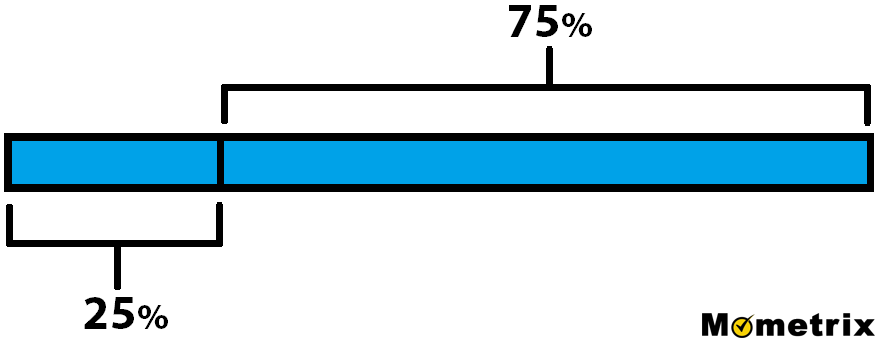
\(\frac{\text{original price}}{100}=\frac{140.67}{75}\)
If \(140.67 = 75\%\), then \(46.89 = 25\%\), by dividing both sides by 3. \(187.56 = 100\%\) by multiplying both sides by 4. The original price was $187.56, so you saved $46.89.
Suppose your friend went shopping with you and used a coupon for an extra 10% off. This coupon was calculated after the total was calculated, so it came off the sale price. What was the total discount percentage from the original price if your friend spent $211.89? Start with \($211.89=90\%\), then if you divide both sides by 9 you get \(23.54=10\%\).
From here, you would multiply both sides by 10 and get \(235.4=100%\). So 100 percent of the sale price equals 75 percent of the original price. So, we have 235.40 is equal to 75 percent of the original price.
From here, if you divide each side by 3, you’ll get \($78.47=25\%\). Then we’ll multiply both sides by 4 to get \($313.87=100\%\). If \(211.89 = 90\%\) of the sale price, then \(23.54 = 10\%\) of the sale price by dividing both sides by 9. This give us \(235.40 = 100\%\).
From here, you would multiply both sides by 10. This give us \(100% of the sale price = 75% of the original price\).
Therefore, if \(235.40 = 75%\) of the original price, then \(78.47 = 25\%\) of the original price by dividing both sides by 3, and \(313.87 = 100\%\) of the original price by multiplying both sides by 4.
We can figure out a percentage by simply dividing the part by the whole, and then multiplying by 100.
In this case, the percentage paid is the amount paid over the original price times 100.
So from the previous example, we have \(\frac{211.89}{313.87}\times 100=67.5\%\). This is the percentage your friend paid. \(100-67.5=32.5\%\), which is the total discount percentage your friend saved. \(100-67.5=32.5\%\), which is the total discount percentage your friend saved.
Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What are proportions?
A
A proportion is a math statement showing that two ratios are equal. This can be written as two equivalent fractions, such as \(\frac{1}{2}=\frac{2}{4}\), or with a colon, such as 1:2 = 2:4. The proportion 1:2 = 2:4 would be read as “one is to two, as two is to four”. Proportions have a wide range of real-world applications, where one missing term is solved for by using cross-multiplication.
For example, suppose you ride your bike 8 miles per hour, and you want to know how long it will take you to bike 40 miles. This can be solved by setting up the proportion \(\frac{8\text{ mi}}{1\text{ hr}}=\frac{40\text{ mi}}{x}\), where we use cross-multiplication to solve for x. \(8(x)=40(1)\), which simplifies to \(x=5\text{ hours}\).
Q
What are the 3 types of proportions?
A
Three common types of proportions are measurements, percents, and rates. Proportions with measurements are often seen in cooking, when a recipe needs to be increased or decreased while maintaining the correct proportions for each ingredient. Proportions with percents are often seen when tipping on a meal. In general, a tip will be proportional to the total meal cost. The more expensive the meal, the higher the tip. Proportions dealing with rates are also very common. For example, if a person drives at 50 miles per hour, we can use proportions to determine how long it will take them to drive 300 miles by setting up a proportion. All of these types of proportion scenarios can be solved by setting two ratios equal to each other, then using cross-multiplication to solve for an unknown value.
Q
How do you solve proportions?
A
In general, proportions are solved using
cross-multiplication
. This means that two ratios are set equal to each other, where one variable is missing. For example, \(\frac{3}{4}=\frac{x}{16}\) shows two fractions that are equivalent, where one piece “x” is unknown. Cross-multiplication refers to the process of multiplying the numerator of the first fraction by the denominator of the second fraction, and multiplying the numerator of the second fraction by the denominator of the first fraction, then setting these numbers equal to each other. This “cross” multiplication process allows us to look at a proportion as a solvable equation. \(\frac{3}{4}=\frac{x}{16}\) becomes \(3(16)=4x\), which simplifies to \(x=12\).
Q
What are examples of proportions?
A
When two ratios are set equal to each other, they are said to be proportional. Proportions are seen in many real-world scenarios where one ration (or fraction) is equivalent to another.
For example:
2:3 = 6:9
\(\frac{15}{30}=\frac{2}{4}\)
20 miles: 1hour = 40 miles: 2 hours
\(\frac{1\text{ cup water}}{4\text{ cups flour}}=\frac{5\text{ cups water}}{20\text{ cups flour}}\)
$24 : 9 pounds = $8 : 3 pounds
Q
Is a proportion a percentage?
A
Percents can be considered proportions because the definition of a percent is “per one-hundred” which itself is a ratio. Percents consist of a “part” and a “whole” that can be set up as a fraction over 100. For example, the percent 45% represents 45 per 100, or \(\frac{45}{100}\) which is a ratio.
Q
What are examples of proportions in real life?
A
Proportions have many real-world applications. For example, say you want to calculate how long it will take you to travel a distance of 450 miles, traveling at a constant speed of 60 miles per hour. This problem can be solved by setting up a proportion, which means setting up two ratios that are equivalent, with one piece missing. 60 miles per hour can be set up as \(\frac{60\text{ mi}}{1\text{ hr}}\). Since we do not know how many hours it will take to travel 450 miles, we will put an x. This becomes \(\frac{450\text{ mi}}{x}\). Now we can set the two ratios equal to each other in order to solve for x \((\frac{60\text{ mi}}{1\text{ hr}}=\frac{450\text{ mi}}{x})\). This can be solved using cross-multiplication. \(x=7.5\), or \(7\frac{1}{2}\) hours.
Q
What are proportions used for?
A
Proportions are used in our daily lives in many ways. For example, doubling a recipe requires the new recipe to have measurements of ingredients that are proportional to the original recipe. Proportions are also used frequently when dealing with cost analysis. For example, if you know that 2 pounds of soil costs $35, you can easily calculate the cost of 400 pounds of soil by setting up a proportion and solving for the unknown value. \(\frac{2\text{ lb}}{$35}=\frac{400\text{ lb}}{$x}\), where x can be solved for using cross-multiplication. \(2x=$14{,}000\), so \(x=$7{,}000\).
What is a Proportion? PDF
Proportion Problems
Which set of ratios are proportional?
The correct answer is \(\frac{3}{4}\) and \(\frac{9}{12}\).
Two ratios are proportional if they are equal in value. The fractions \(\frac{3}{4}\) and \(\frac{9}{12}\) express the same amount, even though they are written in a different form. If we simplify \(\frac{9}{12}\) by dividing the numerator and denominator by 3, we have \(\frac{3}{4}\).
Are the two rectangles below proportional?
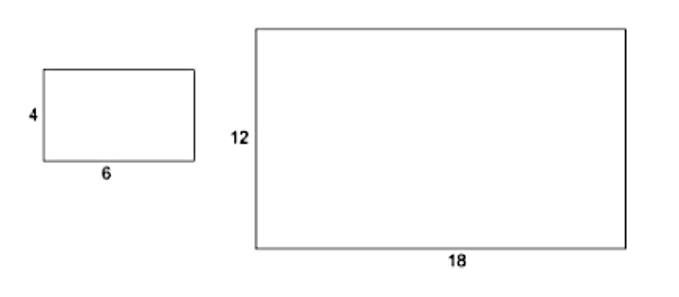
The correct answer is Yes, they are proportional.
We can express the dimensions of each rectangle as a ratio. Let’s represent the smaller rectangle as \(\frac{4}{6}\) and the larger rectangle as \(\frac{12}{18}\). These two ratios are equivalent, so they are considered proportional. \(\frac{12}{18}\) can be simplified to \(\frac{4}{6}\) if we divide the numerator and denominator by 3.
Matt drives his car 62 miles per hour on a 250-mile road trip from Arizona to California. He travels at a consistent speed the entire way. What is the constant of proportionality in this scenario?
The correct answer is 62.
The constant of proportionality is what determines the relationship between y and x in the equation \(y=kx\). In this equation the x-value is directly proportional to the y-value. In this scenario, distance is directly proportional to hours: an increase of 62 miles for every hour. Every hour is multiplied by 62 to calculate distance; therefore, 62 is the constant of proportionality.
Jessica’s dinner bill is $35.80, and she wants to leave a 20% tip. How much should she leave for the tip?
The correct answer is $7.16.
We can set up a proportion in order to calculate a 20% tip on a $35.80 restaurant bill. Our proportion will take the following form: \(\frac{\text{whole amount}}{100}=\frac{\text{partial amount}}{\text{partial percent}}\). Now let’s plug in the values that we know to be true: \(\frac{$35.80}{100}=\frac{x}{20}\) In order to get from 100 to 20 we divided by 5, so let’s also divide $35.80 by 5 in order to determine the unknown tip (x). \(\frac{$35.80}{5}=$7.16\) tip.
James uses a 10% off coupon for a pair of shoes he purchases. With his 10% off coupon the cost of the purchase is only $36. What would the original price of the shoes have been without the coupon?
The correct answer is $40.
If 10% off results in a $36 purchase, we know that 90% of the total cost is $36. If 90% of the total cost is $36, then 10% of the total cost is $4 (divide both by 9). If 10% of the total cost is $4 then 100% of the total cost is $40 (multiply both by 10).