
Hi, and welcome to this video on conditional and absolute inequalities.
Until now, much of the algebra you have learned involved equations, that is, statements showing two mathematical expressions that are equal to one another. For example, when looking at \(3x + 5 = 17\), what is on the left side of the equation, \(3x + 5\), is equal to what is on the right side of the equation, 17.
Comparing Expressions
Sometimes, however, instead of showing that expressions are equal, we want to compare two expressions to show that one is larger or smaller than the other. These types of statements are referred to as inequalities, because we are not aiming to generate two expressions that are equal to one another, as we do with equations. Inequalities portray expressions that are generally not equal.
There are four symbols that allow us to indicate that expressions are larger or smaller than each other.
Less Than (<)
This symbol (<) means “less than.” For example, this means three is less than seven: 3<7. A trick to remembering which side is larger or smaller is that the side of the symbol with the point is “smaller” than the open side, which appears to be “larger”.
Greater Than (>)
The next symbol is >, which means “greater than.” An example would be 8 is greater than 2: 8>2.
The last two symbols are very similar to the first two:
Less Than or Equal To (≤)
This symbol ≤ means “less than or equal to.” It is almost the same as the < sign, but also includes values equal to the number on the right of the sign. For example, if we said [latex]x[/latex]≤3 , [latex]x[/latex] would include values such as 1 and 2, and could also include 3, since 3 is equal to 3.
Greater Than or Equal To (≥)
Similarly, this sign ≥ means “greater than or equal to.” So if we said \(y\)≥6, then \(y\) could include values such as 7, 10, or 22, but it could also include 6, since \(y\) can be equal to 6.
Double Inequalities
Sometimes, you will see inequalities containing more than one of these symbols. These are referred to as double inequalities.
An example would be this 7>\(x\)>2. This suggests that \(x\) is less than 7, but greater than 2. This means that 3, 4, 5, and 6 would all be acceptable values of \(x\).
As you can see, inequalities may contain variables, just like equations. And just as certain values of a variable render an equation correct, so too, certain values of variables render inequalities to be true.
Oftentimes, only certain values of the variable satisfy the inequality, while other values would make it false. These types of inequalities are called conditional inequalities, because they are only true under certain conditions.
Solving Conditional Inequalities
To solve a conditional inequality, treat it as you would a standard equation and solve for the variable.
Example #1
Let’s look at a simple example:
Say you were given \(x + 2 \gt 9\).
The way to figure out the value of \(x\) is to solve this inequality just as you would any other equation. As you may recall, to determine the value of a variable you isolate the variable on one side of the equation, and we do the same thing for an inequality.
So you’re going to subtract 2 from both sides, and you are left with \(x\gt 7\).
This means that any value of \(x\) above 7, not including 7, will make this inequality true.
To quickly check your answer, lets use a value of 4 for \(x\). Plug in 4 plus 2 is greater than 9, you get 6 > 9, which is not true. However, using a value of 8 for \(x\), you can plug in 8 plus 2, is greater than 9, that gives you 10 > 9, which is true. It’s above 7 so that means it’s correct.
Example #2
Let’s try a more complicated example: \(3x – 7 \leq 8 + 2x\).
The first step is to solve for \(x\) as you would with any other equation.
So we’re going to start by adding 7 to both sides, that gives us: \(3x \leq 15 + 2x\). Now we’re going to subtract 2\(x\) from both sides, this leaves us with \(x \leq 15\). That means that any values of \(x\) that are 15 or lower will work for this inequality.
There is one additional rule that you should keep in mind when solving inequalities: whenever an inequality is multiplied or divided by a negative number, the inequality sign needs to be reversed.
Example #3
Here’s a quick example to see this rule in action:
Let’s solve this inequality: \(-2x + 10 \gt 8\).
So we’re going to start by subtracting 10 from both sides, which gives you \(-2x \gt -2\).
In order to isolate \(x\), we divide both sides by -2. This is where our rule comes into play. After dividing by negative two, we would normally be left with \(x \gt 1\), but we reverse the inequality sign, giving us \(x \lt 1\). This means that any value less than 1 will make our inequality correct. To test out our answer, if we use the value 0 for \(x\), we’ll plug it in get 2 times 0, plus 10 is greater than 8. 0 plus 10 is greater than 8, 10 is greater than 8 which is correct.
Example #4
Just as equations can also include absolute values, inequalities may include them as well. In case you need a refresher, an absolute value expresses how far away a number is from zero. It doesn’t matter if the given number is positive or negative.
Say you had \(|x| – 5 \lt 3\)
The first step would be to isolate the absolute value of \(x\). We’d do this by adding 5 to both sides of the inequality.
That gives us \(|x| \lt 8\).
This answer suggests that \(x\) is less than 8 spaces from zero in either direction.
Therefore, we would write the answer as this: \(-8 \lt x \lt 8\)
I hope this review of inequalities has helped! Thanks for watching, and happy studying!
Conditional and Absolute Inequalities Practice
How would we write the following in mathematical terms: “eighty-nine times y is less than or equal to x plus thirty-four” ?
The correct answer is C. “Eighty-nine times y” is written as \(89y\). In this case, the “less than or equal to” sign faces the right* (like this: \(\leq\)). And “x plus thirty-four” is written x+34. Note that we could also write \(x+34≥89y\).
*A helpful hint to remember which way inequality signs face is to think of a <, >, ≤, or ≥ as a mouth. The pointy end will point to the smaller value, while the ‘mouth’ of the symbol opens up towards the greater (larger) value; because it wants to eat the bigger meal!
Which of the following is true:
The correct answer is A because, while 26 may not be less than (nor greater than) 26, it is equal to 26. Notice that we could rewrite this inequality to ‘go in the opposite direction;’ \(26\geq26\) is the same as \(26\leq26\).
Solve for x in the following inequality:
\(\frac{3x+8}{4}-1\) < \(7\)
The correct answer is C: \(x\) < \(8\). We follow the order of operations (remember P.E.M.D.A.S.):
\(\frac{3x+8}{4} –1\) < \(7\)
\((\frac{3x+8}{4} –1)+1\) < \(7+1\)
\(\frac{3x+8}{4}\) < \(8\)
\((\frac{3x+8}{4})×4\) < \(8×4\)
\(3x+8\) < \(32\)
\((3x+8)-8\) < \(32-8\)
\(3x\) < \(24\)
\((3x)÷3\) < \(24÷3\)
\(x\) < \(8\)
Rewrite \(-4\)< \(y\) < \(4\) using only one inequality sign and \(|y|\).
The correct answer is B: \(|y|\) < \(4\). We know that any value which is less than 4 but greater than -4 is a correct solution for y. Consider the number line we make by using \(-4\) < \(y\) < \(4\):
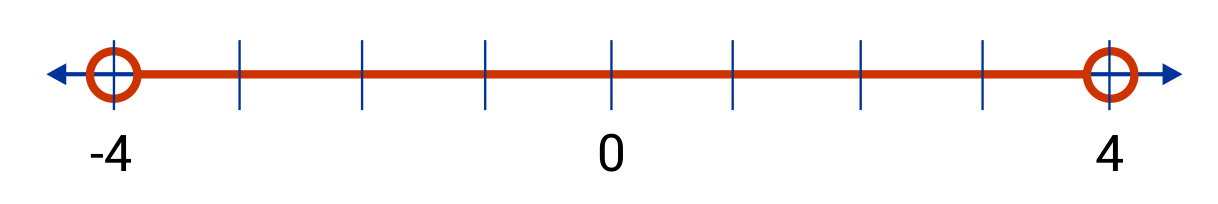
Notice that -4 sits four spaces to the left of the 0 and 4 sits four spaces to the right of the 0. So, no matter which direction we go from 0, we can only choose a y-value that is within 4 spaces from the 0. In terms of integers, this would mean that y could equal -3, -2, -1, 0, 1, 2, or 3.
Solve for x in the following inequality:
\(-4x+3\leq-17\)
The correct answer is A: \(x\geq5\), and we get this from using the order of operations and our inequality sign reversal rule (REMEMBER: any time that we solve an inequality by multiplying/dividing by a negative number on both sides, we must reverse the direction of the inequality sign!). Here’s how we solved it:
\(-4x+3\leq-17\)
\((-4x+3)-3\leq(-17)-3\)
*(note that “\((-17)-3\)” is really \((-17)+(-3)=-20\).)
\(-4x\leq-20\)
\((-4x)\div(-4)\leq-20\div(-4)\)
*(note that (-#)÷(-#)=positive number.)
**(note that we are dividing by -4, so we flip the sign!)
\(x\geq5\)
