Solving Systems by Graphing

In this video, we are going to talk about graphing lines as a method of solving systems of equations.

Whenever we are given a system of two equations, we solve it by finding out which values of \(x\) and \(y\) make both equations simultaneously true. There is more than one way of tackling this type of problem, but the method we are discussing in this video, graphing, is great for visualizing how each equation behaves and then quickly pinpointing the solution.

Let’s start with an example. Determine which values of \(x\) and \(y\) satisfy this system of equations:

To find the solution, let’s draw each of these equations as lines on the Cartesian plane. First, since the equation \(y=2x-5\) is already in the form \(y=mx+b\), we know that it has a slope equal to 2, and a \(y\)-intercept at \(–5\), so it looks like this:

The second equation, \(y=x+3\), is also already slope-intercept form, and we can see that it forms a line with a slope equal to 1, and a \(y\)-intercept at positive 3, so it looks like this:

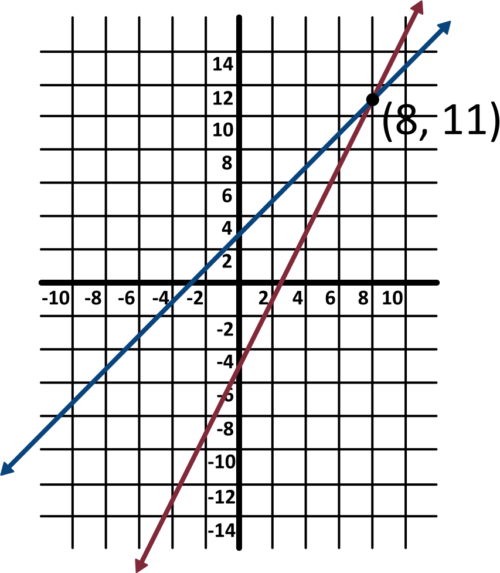
Believe it or not, drawing the lines is the hardest step in this process! All that’s left to do now is see where the lines intersect. Remember, the solution to a system of equations is the values of x and y that make both equations simultaneously true, and the coordinates of the point of intersection will give us exactly that!

Just by looking at this graph, we can easily spot the point of intersection right here at the point 8,11. This tells us that both equations are simultaneously satisfied when \(x=8\) and \(y=11\).

We can check this solution by plugging \(x=8\) and \(y=11\) into both equations given.

As we can see, both of these equations are true for these values, so we know for sure that our solution is correct.

In some cases, the equations given in a system may not be in the form \(y=mx+b\). However, if this is the case, we can easily rearrange them to be in that form so we can graph them as lines. Let’s try an example.

Find the solution \((x,y)\) that satisfies both equations in the following system:

To draw the first equation as a line, we need to convert it into the form \(y=mx+b\), by getting \(y\) on the left side by itself. Subtract \(x\) from both sides to get:

Now that we have the equation written this way, we see that it represents a line with slope of \(–1\) and a \(y\)-intercept at positive 5, which we draw like this:

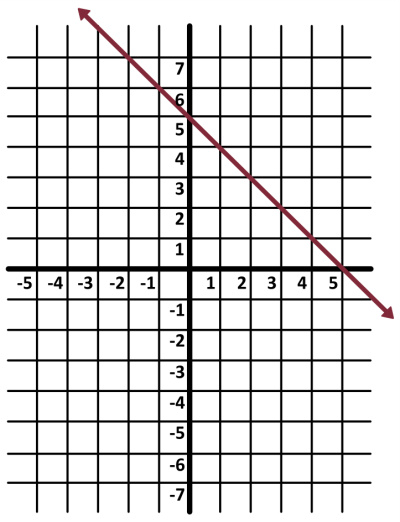
To put the second equation in proper form, first subtract \(4x\) from both sides.

Then, divide both sides by \(–2\) to get y by itself.

So the second line has a slope of 2 and a \(y\)-intercept at \(-\frac{5}{2}\), and we draw it like this:

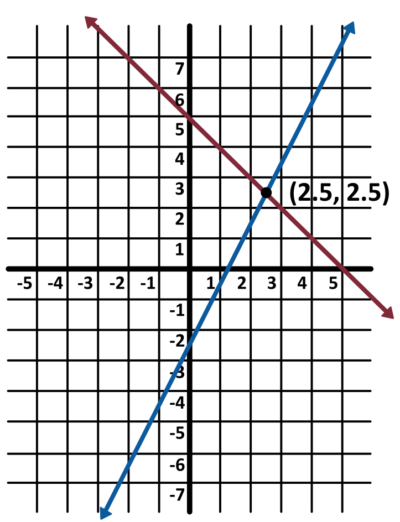
Now that we have both lines drawn, we can once again spot the point of intersection. This time, it’s at the point \((2.5 ,2.5)\), which is our solution.

Let’s wrap up with a real-life example.

Frozen yogurt stores typically charge customers according to the weight in ounces of the yogurt and toppings they select. One store, the Yogurt Moat, charges customers 50 cents per ounce of yogurt and toppings, while another store, Yogurt Yetis, charges a flat starting price of $2.00, plus 25 cents per ounce. Determine how many ounces a customer has to buy for the two stores’ prices to be equal, and then find that price.

Pause the video here and solve this on your own first.

To solve this problem, we need to describe the two stores’ pricing rules as equations. First, the Yogurt Moat charges 50 cents per ounce. So the price, which we will call y, is equal to 0.50 times the number of ounces, which we’ll call \(x\).

The second store, Yogurt Yetis, charges only 25 cents per ounce, but with an additional $2.00 to start with. So we can represent this with this equation.

Rewriting these using fractions and whole numbers, we have this system of equations.

Now we can draw these as lines on the plane. The first line has a slope of 12 and a \(y\)-intercept equal to 0, so it looks like this:

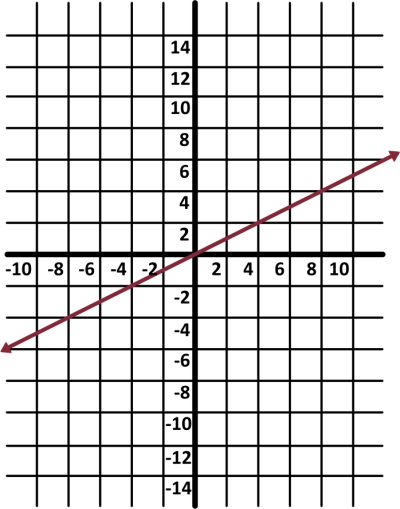
And the second line has a slope of 14 and a \(y\)-intercept at positive 2.

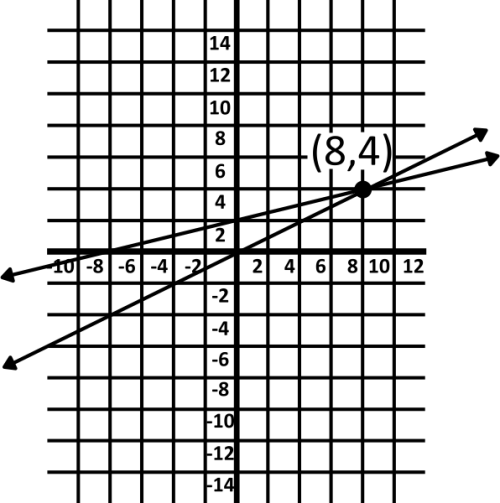
Now we see that the two lines intersect at the point \((8,4)\). Since we said that \(x\) represents number of ounces, and \(y\) represents yogurt price, the two stores have the same price for 8 ounces, at $4.00.

As we have seen, by treating a system of equations as a pair of lines, we can quickly solve for the correct values of \(x\) and \(y\) by plotting the two lines on the Cartesian plane. Just rearrange the equations into the form \(y=mx+b\), plot the lines, and find the point of intersection!

I hope this video on solving systems of equations by graphing was helpful. Thanks for watching, and happy studying!