Evaluating Expressions with Exponents and Roots
In this video, I’m going to talk about exponents and roots. An exponent is a number that tells you how many times to multiply the base number by itself. For instance, if we have 2 raised to the second power, \(2^2\), what this is telling us is that we need to multiply 2 times 2.
Now, if we had 2 raised to the third power,\(2^3\), this would be the same as 2 times 2 times 2. The exponent is saying how many times to multiply this number by itself. A root is kind of the opposite of this. Let’s take, for instance, 16.
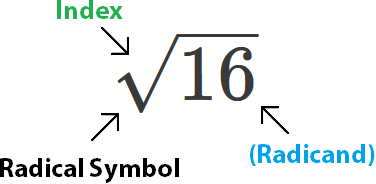
The radical symbol tells us that we’re taking a root.
If there is no number in the index spot, the number is assumed to be 2. Without any numbers there, the radical sign designates a square root, or a root to the power of 2. The square root of 16 is a number that has to be multiplied by itself twice in order to equal 16.
The square root of 16, if it is squared or raised to the second power, it equals 16. The square root of 16 is 4. 4 raised to the second power is equal to 16.
Roots and exponents are kind of inverse operations, but you can actually express roots as exponent.
For instance, if we wanted to go back to the square root of 16, we can write the square root of 16 as 16 to the \(\frac{1}{2}\): \(16^{\frac{1}{2}}\)
Essentially, if you have 1 over a number as an exponent, you’re taking that number’s root of the number in question. Like I was saying, the 2 that’s omitted for a square root, that’s the same as \(\frac{1}{2}\) (the power of \(\frac{1}{2}\)).
You can also have other fractions or other powers of roots. For instance, you might take 8 to the \(\frac{1}{3}\), or third root of 8. This would be a number that you have to multiply by itself three times in order to achieve this. The third power 8 raised to the third power is equal to 8.
This number would be the same as 2, because 2 times 2 times 2, or 2 to the third power, is equal to 8.
A couple other things about exponents. Any number raised to the 1 is just the number itself. 2 raised to the 1 is just 2. Any real number raised to the 0 is equal to 1. It doesn’t matter if it’s a positive number or a negative number. Any real non-zero number raised to the power of 0 is equal to 1.
You may notice that all of the exponents and roots we’ve looked at so far here are whole numbers or fractions of whole numbers.
You can, in fact, have roots that are, for instance, say this is 2 raised to the 2.3. You can have this sort of quantity, but it’s not going to be easy to calculate by hand, and really you’re going to use a calculator if you encounter anything that has a decimal in the exponent.
That’s a good overview of exponents and roots.
