
Hello, and welcome to this video about solutions of a quadratic on a graph!
Today we’ll learn how to find solutions to a quadratic function by looking at its graph. We’ll also talk about how to graph a quadratic equation and analyze the graph to find solutions.
A Review of the Basics
Before we get started, let’s review a few things. First, a quadratic function is a polynomial function, and its highest degree term is of the second degree. The graph of a quadratic function is a two-dimensional curve called a parabola. The parabola can open upward or downward and can vary in width. However, all parabolas share the same U-shape.
A parabola is symmetric over an invisible line called the axis of symmetry. The vertex is the point on the parabola where the graph intersects its axis of symmetry. In the parabola shown, \(y=x^{2}\), the vertex is the point at the bottom of the U-shaped parabola, seen here at point \((0,0)\).
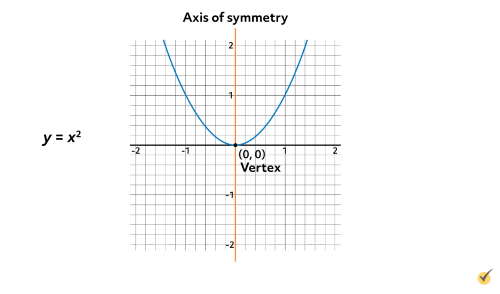
Notice that this parabola is symmetrical with respect to the y-axis, which is the axis of symmetry on this graph. The vertex is the point at the bottom of the U-shape.
If the graph of a quadratic function crosses the x-axis at two points, then the equation has two real rational solutions. These solutions are also called x-intercepts or roots. If it touches the x-axis at one point, it has one real rational solution. If the graph does not intersect the x-axis, then the equation has no real solutions.
A quadratic equation in standard form is written as \(ax^{2}+bx+c=0\), where \(a\neq 0\) and \(a\), \(b\), and \(c\) are all real numbers. We can solve a quadratic equation by factoring, completing the square, using the quadratic formula, or analyzing the graph of its function.
Solving Quadratic Equations with Graphs
Example #1
Consider the graph for \(y=x^{2}+x-6\). We can use this graph to solve the equation \(x^{2}+x-6=0\). Notice that \(y\) is replaced with \(0\). Replacing \(y\) with \(0\) indicates that we are solving for \(x\) by identifying the \(x\)-intercepts.
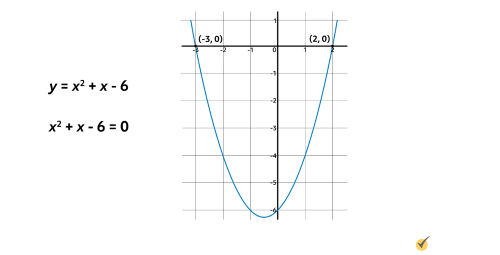
Looking at the graph, we can see that this quadratic function has two solutions. The graph intersects the \(x\)-axis at the points \((-3,0)\) and \((2,0)\), so the solutions for \(x\) are -3 and 2. In this example, there are two real rational solutions. The graph intersects the \(x\)-axis exactly two times.
Example #2
Let’s look at another example. Consider the graph for \(y=-x^{2}+4\). Notice that the value for a is negative, so this parabola opens downward. We can use the graph to solve the equation \(-x^{2}+4=0\).
The graph intersects the \(x\)-axis at points \((-2,0)\) and \((2,0)\), so \(x=-2\), 2. In this example, there are two real rational solutions. The graph intersects the \(x\)-axis exactly two times.
Example #3
Let’s try another one. Consider the graph for \(y=x^{2}-2x+1\). We can use the graph to solve the equation \(x^{2}-2x+1=0\).
Notice that this graph doesn’t pass through the \(x\)-axis. Instead, its vertex touches the \(x\)-axis at the point \((1,0)\). In this case, there is only one real rational solution, \(x=1\).
Example #4
Let’s try one more. Consider the graph for \(y=x^{2}+1\). We can use this graph to identify possible solutions to the equation \(x^{2}+1=0\).
Looking at this graph, we see that it doesn’t pass through the \(x\)-axis at all, which means there are no x-intercepts. In other words, there are no real solutions to this equation.
Quadratic Functions in the Real World
Quadratic functions occur in many real-world situations. Many questions about time, speed, and distance require quadratic equations to solve. An example of this is throwing a ball up into the air. Once a ball is thrown, it slows and eventually falls back down. When thrown, the ball’s path travels in an upside-down U-shape, or parabola. A quadratic equation can be used to find the position of the ball for the amount of time it’s in the air.
Another example is a boat traveling against a river current. If a boat travels 10 miles upstream and turns around to return to its starting point, its path will be in a U-shaped parabola. A quadratic equation can be used to find the boat’s speed and the length of the trip.
There are lots of other problem-solving instances in which quadratic equations are helpful. Understanding them helps us apply mathematical concepts in the real world. Let’s take a look at a story problem that we can solve by graphing a quadratic function.
The width of a rectangular field is 2 meters less than the length. The area is \(48\text{ m}^{2}\). Find the dimensions of the field.
First, start with the formula for the area of a rectangle, which is \(A=\text{ length}\times \text{ width}\). The word problem doesn’t give the field’s length, so use the variable \(x\) to represent length. Since the width is 2 meters less than the length, use the expression \(x-2\) to represent the width.
Next, substitute the values into the area formula. So we said:
We were given that our area is equal to 48, and we said that length is \(x\) and width is \(x-2\).
From here, simplify the equation and write it as a quadratic equation in standard form.
So the 48 is going to stay the same for right now and we’re going to distribute the \(x\) into the parentheses \((x-2)\). So \(x\cdot x=x^{2}\) and \(x\cdot (-2)=-2x\).
Now remember, we want 0 on one side so we’re going to subtract 48 from both sides.
That gives us:
Now remember standard form technically has the 0 on the other side, so we’re just going to rewrite it as:
Now we’re in proper standard form.
Now that we have the area expressed as a quadratic equation, we can create a graph to interpret possible solutions. To graph the parabola, we need the coordinates for its \(x\)-intercepts and its vertex.
Let’s start by identifying the coordinates for the \(x\)-intercepts. We can find these by factoring the equation \(x^{2}-2x-48=0\). Quadratic equations can be factored as \((x-p)(x-q)=0\), where \(p\) and \(q\) are solutions to the equation.
To factor the equation, identify two numbers with a sum of -2 (\(b\)) and a product of -48 (\(c\)). Two numbers with a sum of -2 and a product of -48 are -8 and 6. Therefore, we can factor this quadratic equation by writing it as \((x-8)(x+6)=0\). Now notice that earlier we said that it was \((x-p)(x-q)\), but here we have a plus sign. Well this is really the same as \((x-(-6))\), which then simplifies to \((x+6)\) because of the subtracting a negative.
Next, substitute values for \(x\) that make each equation true. Since \(8-8=0\), \(x=8\). Since \(-6+6=0\), \(x=-6\). The solutions for \(x\) are 8 and -6. So the coordinates for these \(x\)-intercepts are (8,0) and (-6,0). So the function passes through these two points.
Now that we’ve identified the coordinates of the \(x\)-intercepts, we can find the coordinates for the vertex. Start by finding the \(x\)-coordinate of the vertex. Since the vertex is the midpoint of the two x-intercepts, the vertex’s \(x\)-coordinate is the sum of the two \(x\)-intercepts divided by 2. So let’s do that. We have our two x-intercepts, 8 and -6, and to find the average of these two points, we’ll add them together and divide by 2.
So the \(x\)-coordinate of our vertex is 1. To find the \(y\)-coordinate of the vertex, substitute 1 in for \(x\) into our original equation, which is \(y=x^{2}-2x-48\). So if we plug in 1 anywhere we see an \(x\), we’ll get:
\(y=1-2-48\)
\(y=-1-48\)
\(y=-49\)
So our y-coordinate is equal to -49. Therefore, the vertex is at point \((1,-49)\).
Now that we’ve identified the \(x\)-intercepts and the vertex, we can use these points to create a graph. Plot the points and join them by a smooth curve, as shown.
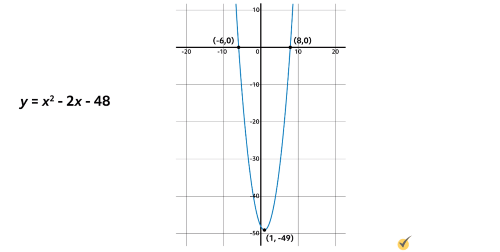
Now that we’ve graphed the function, let’s reconsider the context of the word problem. Recall that we are trying to identify the dimensions of a rectangular field. Since meters can’t be measured in negative numbers, the only solution for \(x\) that makes sense here is 8. Recall that \(x\) represents the field’s length, which is 8 meters. Recall that the width is 2 meters less than the length. Since \(8-2=6\), the width of the field is 6 meters. The field is 8 meters long and 6 meters wide.
Example #5
Now it’s your turn. I’m going to give you a quadratic function and you need to factor it, identify the coordinates for its x-intercepts, identify the coordinates for its vertex, and graph it. This problem is challenging because it involves several steps, but I know you can handle it! The quadratic function is \(y=x^{2}-6x-16\). Pause the video here and try it yourself.
Let’s take a look at this quadratic function together. The first step is factoring the equation \(x^{2}-6x-16=0\). To do so, we need to identify two numbers that have a sum of -6 (\(b\)) and a product of -16 (\(c\)). Then, we’ll write these numbers into the factored equation \((x\text{ })(x\text{ })=0\). The correct numbers are -8 and 2 because \(-8\times 2=-16\), and \(-8+2=-6\). So we’re going to plug in -8 and 2:
Next, substitute a value for \(x\) in both subtraction problems that makes the equation true. Since \(8-8=0\), \(x=8\). Since \(-2+2=0\), \(x=-2\). Therefore, the solutions for \(x\) are 8 and -2. We can write the \(x\)-intercept values as the coordinate points (8,0) and (-2,0).
Now that we’ve identified the \(x\)-intercepts, we need to find the coordinates for the vertex, starting with its \(x\)-coordinate. Recall that the \(x\)-coordinate of the vertex is the midpoint of the \(x\)-intercepts. So for our vertex, to find the \(x\)-coordinate all we have to do is add these two values and divide by 2.
So the \(x\)-coordinate of the vertex is 3. To find the \(y\)-coordinate, substitute 3 for \(x\) into our original equation \(y=x^{2}-6x-16\):
\(y=9-18-16\)
\(y=-9-16\)
\(y=-25\)
Therefore, the vertex is at point \((3,-25)\).
Now that we’ve identified the \(x\)-intercepts and the vertex, we can use points \((8,0)\), \((-2,0)\), and \((3,-25)\) to create a graph. Plot the points and join them by a smooth curve.
I hope this video about solutions of a quadratic on a graph was helpful. Thanks for watching, and happy studying!
Quadratic Equation on a Graph Practice Questions
Solve \(x^2+3x-28=0\) by using the graph shown below:
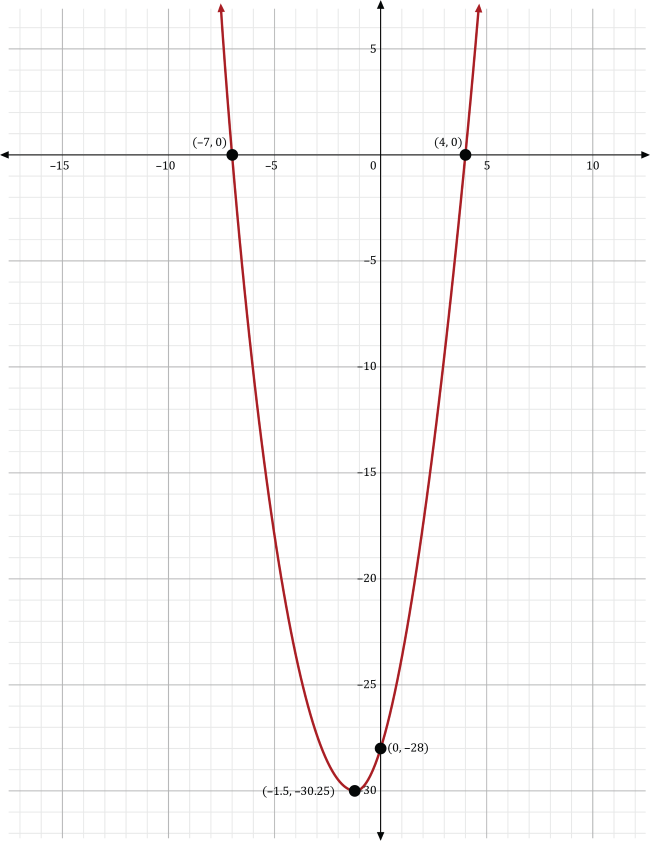
Looking at the graph, we see that the quadratic function crosses the \(x\)-axis at two points. This means that there are two real solutions to this equation. The graph intersects the \(x\)-axis at points \((-7,0)\) and \((4,0)\), so the solutions for \(x\) are –7 and 4.
Solve \(x^2+10x+25=0\) by using the graph shown below:
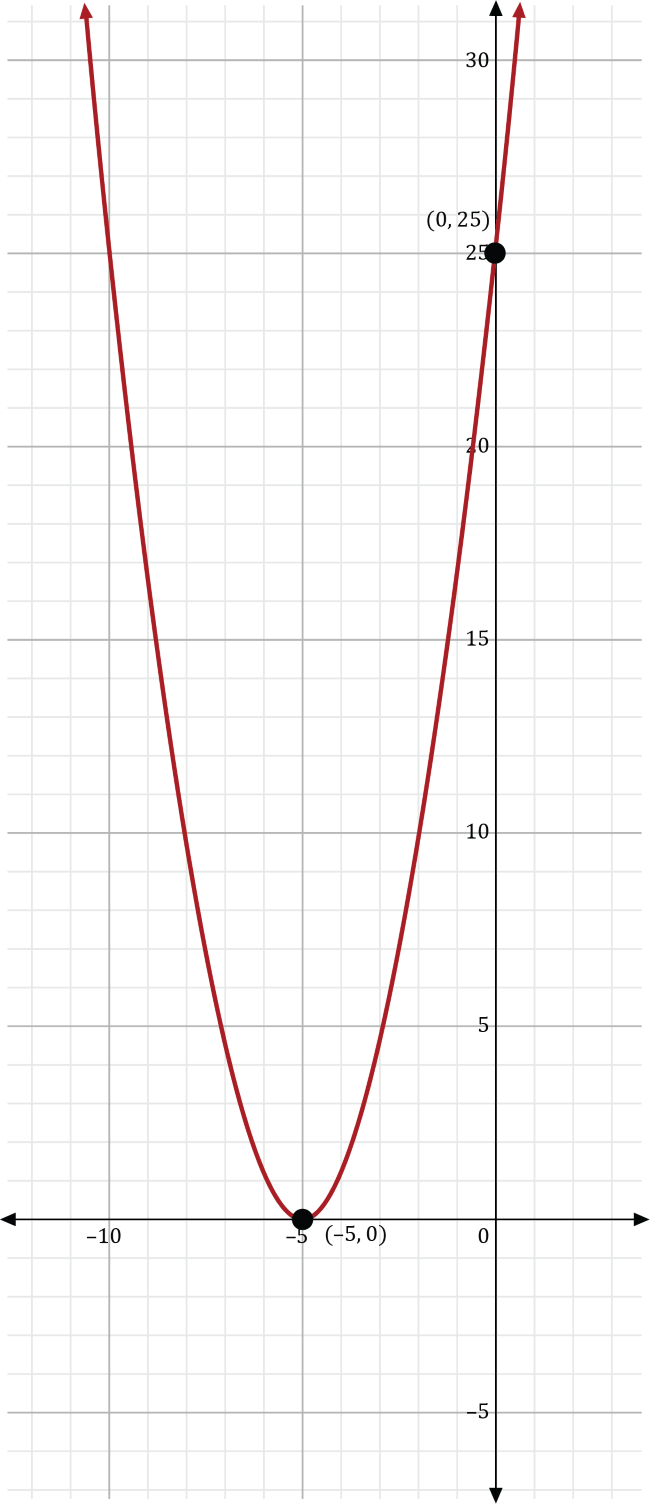
Looking at the graph, we see that the quadratic function touches the \(x\)-axis at exactly one point. This means that there is one real solution to this equation. The vertex touches the \(x\)-axis at point \((-5,0)\), so the solution for \(x\) is –5.
Solve \(x^2+x+4=0\) by using the graph shown below:
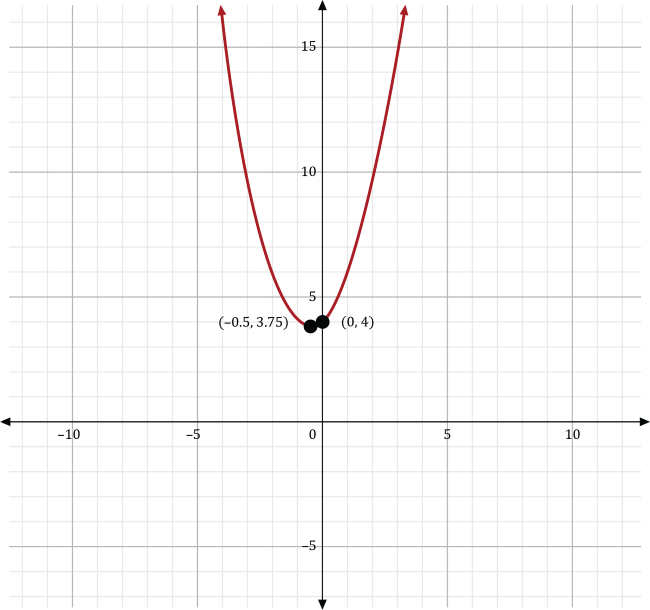
Looking at the graph, we see that the quadratic function does not pass through the \(x\)-axis at all. This means that there are no real solutions to this equation.
The length of a rectangular flag is 4 feet longer than its width. The area is 96 square feet. Find the dimensions of the flag by writing a quadratic equation and graphing it on the coordinate plane.
Start by recalling the formula for the area of a rectangle, which is length times width. Substitute the values from the word problem into this formula. Since the width is not known, use w to represent width. Since the length of the flag is 4 feet longer than its width, use \(w+4\) to represent the length.
\(A=lw\)
\(96=w\left(w+4\right)\)
Next, simplify the equation by distributing \(w\). Write the quadratic equation in standard form.
\(96=w^2+4w\)
\(96-96=w^2+4w-96\)
\(0=w^2+4w-96\)
\(w^2+4w-96=0\)
Then, identify the coordinates for the \(x\)-intercepts. Factor the equation by finding two numbers that result in a sum of 4 and a product of -96. These numbers are 12 and -8.
\(\left(w+12\right)\left(w-8\right)=0\)
From here, equate each binomial to 0 and solve for \(w\). The solutions are -12 or 8. The coordinates for these \(x\)-intercepts are \((-12,0)\) and \((8,0)\). The graph of the function passes through the \(x\)-axis at -12 and 8.
\(w+12=0\hspace{20 mm}w-8=0\)
\(w=-12\hspace{20 mm}w=8\)
Now that we know the \(x\)-intercepts, find the coordinates for the vertex, \((h,k)\). Start by finding \(h\), which is the vertex’s \(x\)-coordinate. Divide the sum of the \(x\)-intercepts by 2:
\(h=\frac{-12+8}{2}=-\frac{4}{2}=-2\)
Next, find \(k\), which is the vertex’s \(y\)-coordinate. Substitute -2 into the quadratic equation for \(w\) and simplify:
\(k=(-2)^2+4\left(-2\right)-96\)
\(k=4-8-96\)
\(k=-100\)
The vertex of this function is \((-2,-100)\). Plot the vertex and the \(x\)-intercepts onto the coordinate plane and join the points with a smooth curve.
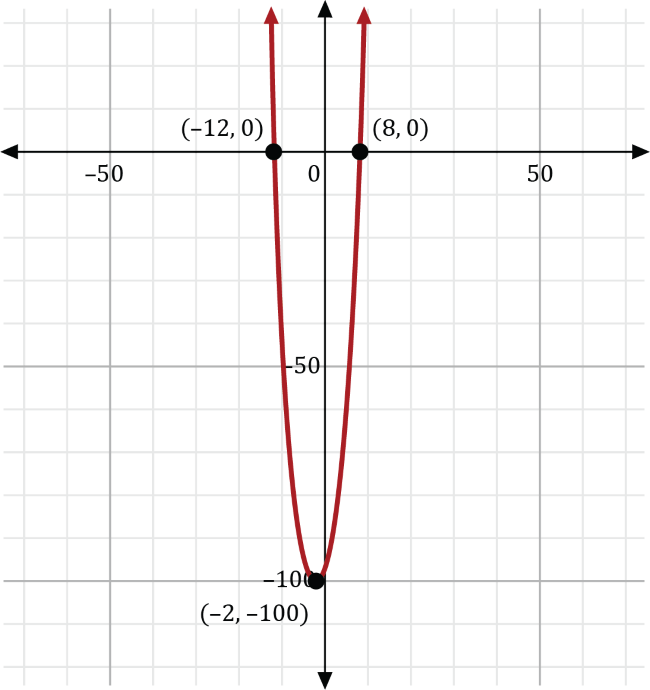
Since this problem is about the area of a flag, the negative solution, -12, does not apply to this scenario. Therefore, the width of the flag is 8 feet. Since the length of the flag is 4 feet longer than its width, the length of the flag is 12 feet.
Nicole drops a ball from 4 feet above the ground and watches as it bounces back into the air. The path of Nicole’s ball takes the shape of a parabola and can be represented by the equation \(\left(x-2\right)^2=0\). Graph this quadratic function to figure out the location of where the ball hits the ground in relation to where Nicole is standing.
Start by writing the quadratic equation as two binomials.
\(\left(x-2\right)^2=0\)
\(\left(x-2\right)\left(x-2\right)=0\)
Next, set each binomial equal to 0 and solve for \(x\). Since both binomials are the same, there is one solution, which is 2. The graph touches the \(x\)-axis at \((2,0)\).
\(x-2=0\)
\(x=2\)
Then, identify the \(y\)-intercept. Since the value of \(c\) in the expanded equation is 4, the \(y\)-intercept is 4. Nicole drops the ball from 4 feet above the ground, so the point representing the \(y\)-intercept is \((0,4)\).
\(\left(x-2\right)\left(x-2\right)=0\)
\(x^2-2x-2x+4=0\)
\(x^2-4x+4=0\)
\(c=4\)
From here, plot the \(x-\) and \(y\)-intercepts onto the coordinate plane and join the points with a smooth curve:
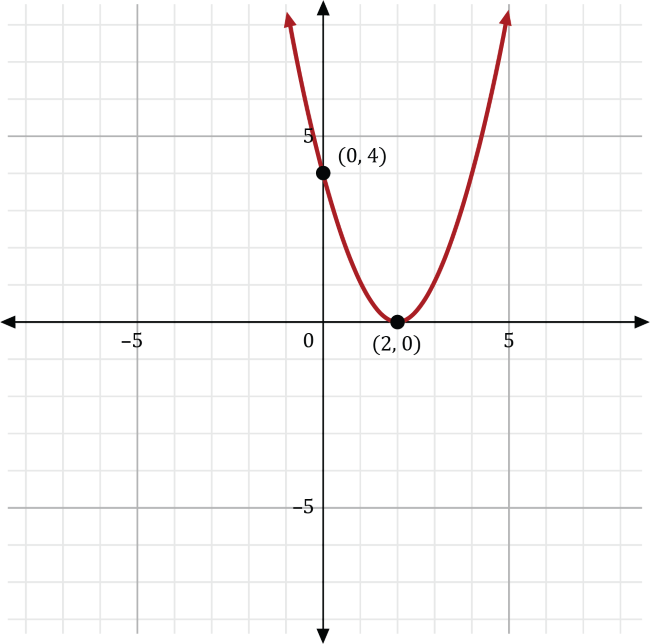
Based on this information, Nicole stands at point \((0,0)\) and drops the ball from 4 feet above ground at point \((0,4)\). The ball hits the ground at point \((2,0)\). Therefore, the ball hits the ground 2 feet away from where Nicole stands.
