
Hi, and welcome to this video on the process of completing the square!
This algebraic process is important in the study of quadratic equations and their key features. Specifically, completing the square helps us to identify the vertex of a quadratic graph and allows us to find the roots of a quadratic equation using the “square root” method.
In this video, we will explore this process and work through some example problems to give you some practice.
Reviewing Quadratic Functions
As mentioned, the process of completing the square allows us to identify the vertex of a quadratic, which is either the maximum or minimum value of the function. Before we attack the process, let’s review the basics of quadratic functions and their graphs.
Graphs of quadratic functions are called parabolas. The vertex of a parabola is either the maximum or minimum value of the function. If the parabola opens “up”, the vertex is the minimum point of the function and can be visualized as the bottom of a valley. If the function opens “down”, the vertex is the maximum point of the function, as if it were on the top of a hill.
There are many applications that require the knowledge of where a function is at its maximum or minimum value, so being able to identify this point quickly is an important skill.
Quadratic equations are typically written in standard form, \(y=ax^2+bx+c\), where \(c\) is a constant that identifies the y-intercept of the graph at \((0,c)\). This point is useful for graphing the function, but it does not tell us where the graph will reach its maximum or minimum value.
This is where the “completing the square” process comes in.
Completing the Square
The process of completing the square results in a quadratic written in vertex form. As the name suggests, it is the vertex, notated \((h,k)\), that is clearly identifiable: \(y=a(x-h)^2+k\).
Example #1
Consider this visual for the standard-form quadratic expression \(x^2+6x+2\):
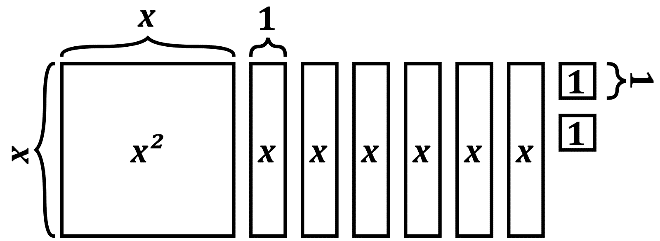
Do you see how this relates to the expression? The leading term is \(x^2\), there are a total of six \(x\)-terms, and there are two “1” terms.
Suppose we were asked to change this rectangular arrangement to take the shape of a square. Well, because there are six \(x\)-terms, we could move half of them below the \(x^2\), as shown here:
We can also move the two 1s into place to fill in the lower right corner of the square. But there aren’t enough 1 terms! In order to complete the square configuration, we would have to add seven additional 1s.
We have created a perfect square, but now we have to account for the seven 1s that we had to add in order to complete the square. Fortunately, it is a simple adjustment of subtracting the seven “1’s” from the squared binomial, like so: \((x+3)^2-7\). In other words, we would add 7 to create a perfect square, but then we had to subtract 7 to keep the expressions equivalent.
The result is the vertex form of the quadratic expression \((x+3)^2-7\).
To check our work, we simplify the vertex form expression as follows:
- Step 1: Expand the squared binomial term.
Our vertex form was: \((x+3)^2-7\).So we wanna expand the \((x+3)^2\) to be \((x+3)(x+3)-7\). - Step 2: Multiply the binomials.
We’ll get \(x^2+3x+3x+9-7\). - Step 3: Combine like terms in the expression.
Doing so results in \(x^2+3x+3x+9-7\).
Here we can combine our \(3x\) and our \(3x\), so we’ll have \(x^2+6x\), and then 9-7 is +2.
This result is the original standard-form expression, so we know that our work is correct!
Example #2
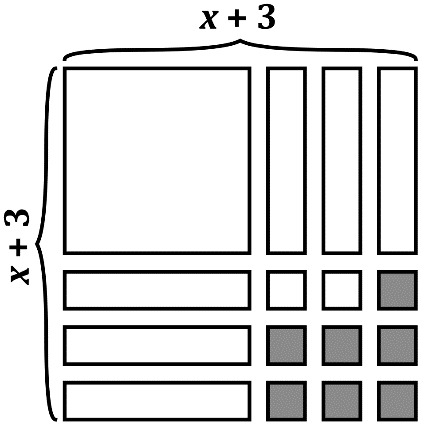
Here is another visual example problem for you to check your understanding of the completing the square process.
First, we need to write the standard form quadratic expression that matches this visual.
Then, we need to figure out how many yellow boxes are needed to complete the square. In this case, it’s two.
Now, we need to write the vertex-form quadratic expression. Remember, we’ll need to adjust the expression to remove the yellow blocks that were needed to complete the square!
So this gives us \((x+2)^2-2\).
Finally, let’s check our work by multiplying the binomials and combining like terms. We have our \((x+2)^2-2\), which we then expand out to be \((x+2)(x+2)-2\). We FOIL to multiply these two expressions out.
And simplify. \(x^2\) plus, \(2x+2x\) gives us \(4x\), and 4-2 gives us +2.
As we can see, our answer does match the standard-form result.
Now let’s tackle the algebraic work of completing the square. The goal is to create a “perfect square trinomial” from the coefficients of the standard form quadratic. Perfect square trinomials factor to either \((x+h)^2\) or \((x-h)^2\), where \(h\) is the coefficient of the \(x\)-term divided in half.
Let’s practice building a perfect square trinomial before moving on. Suppose you have a quadratic expression, \(x^2+6x\). In order to create the perfect square trinomial, we divide the coefficient of the \(x\)-term by 2 and square the result, \(\frac{6}{2}^2\), for a value of 9. When we add this value to the original expression, we have a perfect square trinomial, \(x^2+6x+9\), which factors to \((x+3)^2\). Recall that this is the same strategy that was used with the visual representation of completing the square. We would’ve had to add nine 1s to complete the lower right corner of the square.
Now for the adjustment for adding those 9 squares: Just as we did before, simply subtract the value that was added from the squared binomial, \((x+3)^2-9\). You have just converted a standard-form quadratic expression into vertex form!
Example #3
Let’s work through another example problem.
Rewrite the standard form quadratic equation, \(y=x^2-4x-7\), in vertex form by completing the square.
First, identify the coefficients \(a\), \(b\), and the constant, \(c\).
For now, we will ignore the constant, -7, and create the perfect square trinomial with the \(x^2\) and \(-4x\) terms.
Next, determine the value needed to create the perfect square trinomial,\((\frac{-4}{2})^2\), which simplifies to \((-2)^2\), which equals 4.
Now, add 4 to the first two terms to create the perfect square: \(y=x^2-4x+4-7\)
Then, factor the perfect square trinomial that you created: \(y=(x-2)^2-7\)
Adjust the expression by subtracting 4 \(y=(x-2)^2-7-4\)
Finally, simplify to show the quadratic equation in vertex form: \(y=(x-2)^2-11\)
Matching up this vertex form equation with the general form, \(y=a(x-h)^2+k\), indicates that the coefficient, \(a=1\), and the vertex of the parabola is at the ordered pair, \((2,-11)\). Because \(a\gt 0\), the parabola opens “up,” meaning that the vertex is the minimum value of the function. As you can probably guess, when \(a \lt 0\), the parabola opens “down.”
Example #4
Here is another example of creating a perfect square trinomial with an added feature of a coefficient in the leading term. Note how the adjustment is made to account for the coefficient!
Convert the standard form equation, \(y=2x^2-8x+3\), to vertex form.
Like before, we will ignore the constant, 3, and work with the first two terms. This time, the terms share a greatest common factor of 2. This value must be factored out before the perfect square trinomial is created:
\(2(x^2-4x+?)\)
Now the value that is needed to complete the square can be determined. Consider the terms inside the parentheses for this to work. As before, cut the coefficient of the \(x\)-term in half and square the result: \((\frac{-4}{2})^2\) or \((-2)^2\) which equals 4.
Let’s rewrite the equation as it stands now:
Can you guess how the equation has to be adjusted? You might guess that we should subtract 4, but look closely.
Because we factored out a 2 in the first step, the four that we added to complete the square within the parentheses actually added \(2\times 4=8\) to the equation! As a result, we must subtract 8 to keep the vertex form equation equivalent to the original standard form equation:
To finish, factor the perfect square trinomial and simplify:
\(y=2(x-2)^2-5\)
In this example, \(a=2\) which, because it is greater than zero, tells us that the parabola opens “up.” The vertex, therefore, is the minimum value of the function and is found at the ordered pair, \((2,-5)\).
As mentioned at the beginning of this video, this process can also come in handy when we are asked to find the “roots” or “zeros” of quadratic equations. These terms are just different ways of referring to the solutions.
When we solve any equation, we are searching for the points on the \(x\)-axis where the graph touches or crosses.
We can see here that a parabola can cross the \(x\)-axis at two points, one point, or not at all! This means that quadratic equations can have two, one “repeating,” or zero real solutions. The solutions for the quadratics that “float” above or below the \(x\)-axis do exist, but they are in the complex number system, which is beyond the scope of this video.
During your work with solving quadratic equations, you learned that there are several methods to choose from. The sure-fire method for solving all quadratics is the quadratic formula, but other methods are sometimes preferred, like factoring or by taking the square root.
That is where the completing the square process comes in! If a standard form quadratic is not factorable and you really do not enjoy using the quadratic formula, you can use the completing the square process to convert from standard form to vertex form and use the square root method to solve.
When you have an equation set to “0” you are being asked to find the value(s) of \(x\) where the equation is equal to zero. Those are the point(s) where the parabola crosses the \(x\)-axis. When you are working with a vertex-form quadratic, solving is just a matter of a few algebraic steps.
Let’s work through our last two example problems together:
Example #5
Solve for \(x\): \(0=(x-5)^2-25\)
- Step 1: Add 25 to both sides of the equation.\(0=(x-5)2-25\)
\(+25\) on each side
\(25=(x-5)^2\)
- Step 2: Take the square root of both sides of the equation.\(25=(x-5)^2\)
\(5=x-5\)
- Recall that taking the square root of 25 results in two values, 5 and -5.
- Step 3: Add 5 to both sides to determine the two solutions of the equation.\(5=x-5\)
\(+5\) on both sides
\(x=55\)
\(x=(5+5)\text{ and }x=(5-5)\)
\(x=10\text{ and }x=0\)
With solutions of \(x=10\) and \(x=0\), we now know that the parabola crosses the \(x\)-axis at the points, \((10,0)\) and \((0,0)\).
Example #6
Here’s our last example:
This example involves one additional step because \(a=-3\). Start the same way, by isolating the \(x\)-variable:
- Step 1: Subtract 6 from both sides of the equation.\(0= -3(x+2)^2+6\)
\(-6\) on both sides
\(-6= -3(x+2)^2\)
- Step 2: Divide both sides by the coefficient \(a=-3\).\(\frac{-6}{-3}=\frac{-3(x+2)^2}{-3}\)
\(2=(x+2)^2\)
- Step 3: Take the square root of both sides of the equation.\(\sqrt{2}=\sqrt{(x+2)^2}\)
\(\pm \sqrt{2}=x+2\)
- Step 4: Subtract 2 from both sides.\(\pm \sqrt{2}=x+2\)
\(-2\) on both sides
\(x= -2\pm \sqrt{2}\)
In most cases, leaving the answer in radical form is acceptable. This parabola crosses the \(x\)-axis at two points, \((-2+2, 0)\) and \((-2-2,0)\).
Let’s take this example a step further! Given the vertex form equation, \(y=-3(x+2)^2+6\), see if you can name the vertex and state whether it is a maximum or minimum value of the function.
Remember that the general vertex form equation is \(y=a(x-h)^2+k\). The coefficient, \(a\), determines whether the parabola opens “up” or “down”, and the vertex is at \((h,k)\). Pause the video if you need more time to think about it.
Because \(a=-3\) and \(a \lt 0\), the parabola opens “down”, so the vertex is the maximum value of the function. The vertex is at the ordered pair, \((-2, 6)\). Remember to change the sign of \(h\) when naming the vertex!
That’s all for this review! Remember, this algebraic process is important when identifying the vertex of a quadratic graph, and it allows us to find the roots of a quadratic equation by using the “square root” method. I hope this review was helpful! Thanks for watching, and happy studying!
Completing the Square Problems
The process of completing the square is a method used to solve quadratic equations by changing the quadratic from standard form to _________ form.
Normally you will see quadratic equations in standard form \(y=ax^2+bx+c\). However, quadratic equations can also be written in vertex form. The benefit of vertex form is that the vertex of the parabola \((h,k)\) is clearly identifiable. Vertex form: \(y=a(x-h)^2+k\)
The following quadratic is written in vertex form. What is the vertex of the parabola?
\(y=5(x-3)^2+15\)
The vertex \((h,k)\) can be located in the quadratic equation \(y=5(x-3)^2+15\) simply by looking at the location of h and the location of k. This equation is in vertex form \(y=a(x-h)^2+k\), which means that 3 is in the location of h, and 15 is in the location of k. This means that \(h=3\) and \(k=15\): \((h,k)=(3,15)\).
Convert the following quadratic equation from standard form to vertex form.
\(y=x^2+12x+32\)
\(y=x^2+12x+32\) is currently in standard form. If we convert this to vertex form the vertex \((h,k)\) will be easy to identify.
Original equation: \(y=x^2+12x+32\)
Step 1: Complete the square
\(y+?=(x^2+12x+?)+32\)
The ? is determined by dividing the 12 by 2, and then squaring it. \(\frac{12}{2}=6\) and 6 squared is 36.
\(y+?=(x^2+12x+?)+32\) becomes \(y+36=(x^2+12x+36)+32\)
Step 2: Rewrite \((x^2+12x+36)\) as a binomial squared.
\(x^2+12x+36\) becomes \((x+6)^2\)
Now the entire equation is \(y+36=(x+6)^2+32\).
One more step and the equation is in vertex form. Subtract 36 from both sides so \(y+36=(x+6)^2+32\) becomes \(y=(x+6)^2-4\). The equation is now in vertex form.
Will the following parabola open up or down?
\(y=2x^2+4x-1\)
If the leading coefficient is greater than zero, the parabola opens up. If the leading coefficient is less than zero, the parabola opens down. The leading coefficient is a in standard form: \(y=ax^2+bx+c\).
In the equation \(y=2x^2+4x-1\) the value of a is greater than zero, so the parabola will open up.
Find the vertex by completing the square.
\(y=x^2-10x+22\)
\(y=x^2-10x+22\) is currently in standard form. If we convert this to vertex form the vertex \((h,k)\) will be easy to identify.
Original equation: \(y=x^2-10x+22\)
Step 1: Complete the square
\(y+?=(x^2-10x+?)+22\)
The ? is determined by dividing the 10 by 2, and then squaring it. \(\frac{10}{2}=5\) and 5 squared is 25.
\(y+?=(x^2-10x+?)+22\) becomes \(y+25=(x^2-10x+25)+22\)
Step 2: Rewrite \((x^2-10x+25)\) as a binomial squared.
\((x^2-10x+25)\) becomes \((x-5)^2\)
Now the entire equation is \(y+25=(x-5)^2+22\).
One more step and the equation is in vertex form. Subtract 25 from both sides so \(y+25=(x-5)^2+22\) becomes \(y=(x-5)^2-3\).
The equation is now in vertex form, and \((h,k)\) can be identified. The vertex of the parabola is \((5,-3)\).
