
Hi, and welcome to this video about the algebra of polynomial and rational expressions! In this video we will explore:
- Multiplying polynomials
- Factoring polynomials
- Dividing polynomials
- Rational expressions
- Operations with rational expressions
A Review of Polynomials
Before we get heavily into polynomial algebra, let’s recap a few important terms.
A polynomial is a mathematical expression of one or more algebraic terms, each of which consists of a constant multiplied by one or more variables raised to a non-negative integral power (such as \(a+bx+cx^2\)).
The key pieces to remember are:
- Polynomials consist of one or more terms (of the general form \(ax^n\)) that are added or subtracted. The sample in the definition has 3 terms.
- The coefficients of the terms can be any type of number.
- The powers of the terms can only be non-negative integers (including 0).
Let’s look at some quick examples:
- \(2x^2-4x+5\) is a polynomial expression, but \(2x^{2.5}-4x+5\) is NOT a polynomial expression. Why? Because of the decimal exponent. Remember, the exponents in a polynomial expression have to be integers.
- \(0.4x+1\) is a polynomial expression, but \(x^{-3}+1\) is NOT, because of the negative exponent.
Types of Polynomial Expressions
Now that we’ve looked at some polynomial expressions, let’s look at the different types:
- A monomial is a polynomial consisting of 1 term. For example, \(x\) and 2 are monomials.
- A binomial is a polynomial consisting of 2 terms. \(x + 1\) and \(x^3+4\) are binomials.
- A trinomial is a polynomial consisting of 3 terms. \(12x^4+3x^3+1\) is a trinomial.
- A degree is the highest exponent in a polynomial.
- 2 is a degree-0 polynomial
- \(x+2\) is a degree-1 polynomial
- \(x^2+3\) is a degree-2 polynomial
Now let’s move on to multiplying!
Multiplying Polynomials
One of the traditional methods taught for multiplying polynomials is FOIL. This method highlights the need for organization.
Multiplying polynomials is an application of the distributive property. The key idea is that every term of each polynomial needs to be multiplied by every term of every other polynomial.
One way to help visualize and organize polynomial multiplication is with an area model, which looks like this. Let’s multiply \(3x+4\) by \(-2x+-5\):
| \(3x\) | \(4\) | |||
| \(-2x\) | \((3x)(2x)\) \(-6x^2\) | \((4)(-2x)\) \(-8x\) | ||
| \(-5\) | \((3x)(-5)\) \(15x\) | \((4)(-5)\) \(-20\) | ||
So the product is \(-6x^2-8x-15x-20\), which then simplifies to \(-6x^2-23x-20\).
The area model demonstrates how to multiply every term of one polynomial by every term of the other and it is expandable for polynomials of any size. Let’s try another example.
| \(2a^3\) | \(-4a^2\) | \(+a\) | \(-12\) | |||
| \(7b^5\) | \(14a^3b^5\) | \(-28a^2b^5\) | \(7ab^5\) | \(-84b^5\) | ||
| \(-2b^2\) | \(-4a^3b^2\) | \(8a^2b^2\) | \(-2ab^2\) | \(24b^2\) | ||
Our terms on the left are \(7b^5\) and \(-2b^2\), and our terms on top are \(2a^3\), \(-4a^2\), \(a\), and \(-12\). We need to simply multiply all the terms, then add the resulting terms together.
None of these are like terms, so they can’t be combined. So our answer is:
So this is our final answer.
Factoring
As we’ll see throughout this video, working with polynomials is almost identical to working with simple numbers. When we think of factors, for example, we may think of numbers that are multiplied to create another number. For example, 2 and 3 are factors of 6. 20 and 5 are factors of 100.
Often, we look for numbers’ prime factorizations. The prime factorization of 30 is \(2(3)(5)\) because all the factors are prime numbers. Think of factoring as undoing the area model we just explored.
Often, the terms of polynomials have common factors.
Consider this polynomial:
Each term has a common factor of \(5a^2\): \((5a^2)(4b) + (5a^2)(2a)\) \(+ (5a^2)(3b^3) + (5a^2)(1)\). So this can be rewritten as \(5a^2(4b + 2a + 3b^3 + 1)\). This is the prime factorization of the polynomial. It cannot be factored any further.
Sometimes, factoring happens in groups. It appears as if this polynomial cannot be factored:
Rearranging to group the \(a\) terms and the \(b\) terms, we have
Pulling out common factors, we have
Now we can see the common factor of \(2x + 1\), so we have this:
We can always check our factoring work by multiplying the factors to be sure we end up with the original polynomial.
Dividing Polynomials
Polynomial division is closely related to multiplication and factoring. Consider the number 6. Its prime factors are 2 and 3. \(2 \times 3 = 6\), so 6 divided by 2 is 3 and 6 divided by 3 is 2.
This polynomial \(-6x^2 – 23x – 20\) has prime factors \((3x+4)\) and \((-2x-5)\).
and
\(\frac{(-6x^2 – 23x – 20)}{(-2x-5)} = (3x+4)\)
One polynomial can be divided by another as long as the degree of the dividend is greater than or equal to the degree of the divisor. Here’s how it works:
Make sure the exponents of both polynomials are in descending order and put a 0 in for any missing in the sequence (for example, \(2x^2 + 1\) would become \(2x^2 + 0x + 1\)).
Divide the first terms. Here, the question is “how many times does \(3x\) go into \(-6x^2\)?”
Multiply \(3x+4\) by \(-2x^2\).
Subtract the product.
Bring down the next term in the divisor.
Repeat. How many times does \(3x\) go into \(-15x\)?
Multiply.
Subtract.
There’s a remainder of 0, so \(-2x – 5\) and \(3x + 4\) are factors of \(-6x^2-23x-20\), as we already knew.
Rational Expressions
Rational expressions are closely related to rational numbers. The word rational comes from the word ratio. Just as rational numbers are defined as having the form integer/integer, rational expressions are defined by the form polynomial/polynomial.
Here are some examples of rational expressions: \(\frac{x^2+2}{3x}, \frac{1}{4a^2}, \frac{4z^4-z^3-10z+2}{11z^5-22z^3}\)
When common factors occur in the numerator and denominator of a rational function, they can be divided to make 1. This is often taught as “canceling out”, but it actually stems from the fact that, for example, \(\frac{2}{2} = 1\).
We can remove the common factors from these rational expressions:
\(\frac{x^2+2x+1}{x^2+3x+2}=\frac{(x+1)(x+1)}{(x+1)(x+2)}=\frac{x+1}{x+2}\)
Rational expressions behave like fractions. To add or subtract them, we need to get a common denominator. For example:
Since one expression has \(3x\) as a denominator and the other has \(x^2\), a common denominator of \((3x)(x2)\) can be created.
Remember to multiply each numerator by the same factor so that we are essentially multiplying each expression by 1.
Now multiply through and simplify.
To multiply them, we multiply straight across. For example:
And to divide them, we multiply by the reciprocal:
And there you have it! I hope this video has increased your understanding of polynomial expressions.
Thanks for watching, and happy studying!
Polynomial Practice Questions
Multiply the following polynomials using the FOIL method. \((3x+2)(x−1)\)
The FOIL method reminds us to multiply polynomials in the order of “First, Outer, Inner, Last”. This ensures that we do not miss any terms when distributing.
F: “First term times First term”
O: “Outer term times Outer term”
I: “Inner term times Inner term”
L: “Last term times Last term”
F: \(3x×x=3x^2\)
O: \(3x×−1=−3x\)
I: \(2×x=2x\)
L: \(2×(-1)=−2\)
\(3x^2-3x+2x-2\) simplifies to \(3x^2-x-2\).
Factor the following polynomial: \(6x^2+13x+6\)
The polynomial \(6x^2+13x+6\) can factored into \((2x+3)(3x+2)\) because when \((2x+3)\) is multiplied by \((3x+2)\) the product is \(6x^2+13x+6\).
When factoring this polynomial, first set up two empty sets of parentheses that are multiplied by each other ( )( )
Now look at the first term \(6x^2\). This can be factored into \(3x\) times \(2x\) because the product is still \(6x\). Now we have \((2x\text{ })(3x\text{ })\).
Now look at the other two terms from the original polynomial: \(13x + 6\). Ask yourself “What two numbers will multiply to 6, but combine to \(13x\) when distributed?”
2 and 3 will multiply to 6, and when distributed using FOIL, they will combine to \(13x\). So our factors now become: \((2x+3)(3x+2)\).
Divide the following polynomials: \((x^2+11x+10)\div(x+1)\)
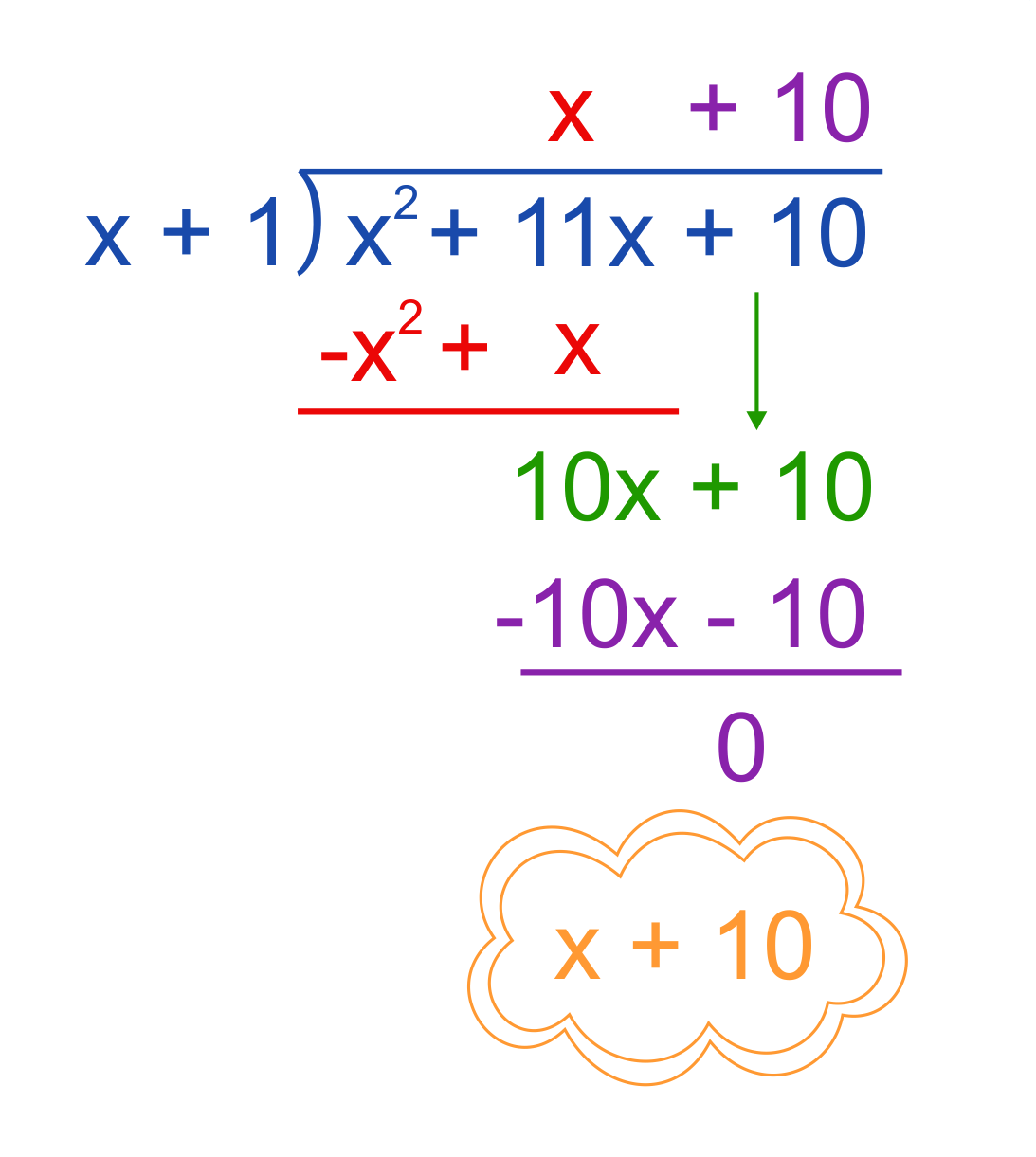
The process follows the same procedures as long division. The answer can be checked by multiplying \((x+1)(x+10)\). The product will be \((x^2+11x+10)\), so we know that the two factors are correct.
Simplify the expression by removing the common factors.
\(\frac{(2x^2+5x-3)}{(6x^2+18x)}\)
\((2x^2+5x-3)\) can be factored into \((2x−1)(x+3)\).
\((6x^2+18x)\) can be factored into \(6x(x+3)\).
Both have the common factor of \((x+3)\), so when divided, this portion will cancel out. When \(\frac{(x+3)}{(x+3)}\) cancels out, \(\frac{(2x-1)}{6x}\) is all that remains.
Simplify the polynomial by multiplying.
\(4x(x^2+3)\)
To simplify the polynomial we can distribute the term \(4x\) into each term within the parenthesis.
\(4x×x^2=4x^3\)
\(4x×3=12x\)
The product of \(4x(x^2+3)\) is \(4x^3+12x\).
