
Hey guys! Today, we are going to dive into the topic of compound inequalities.
What is a Compound Inequality
A compound inequality contains at least two inequalities and is separated either by an “or” or an “and.” Compound inequalities can be used to describe real-world situations, such as the years that a person is not working.
“Or” Inequality
For example, most people are not working below age 18, or above age 65. This can be represented by the compound inequality \(x\lt 18\text{ or}\text{ }x\gt 65\). This states that people (\(x\)) generally will not be working at an age that is less than 18, OR an age that is greater than 65.
This is an example of an “or” inequality.
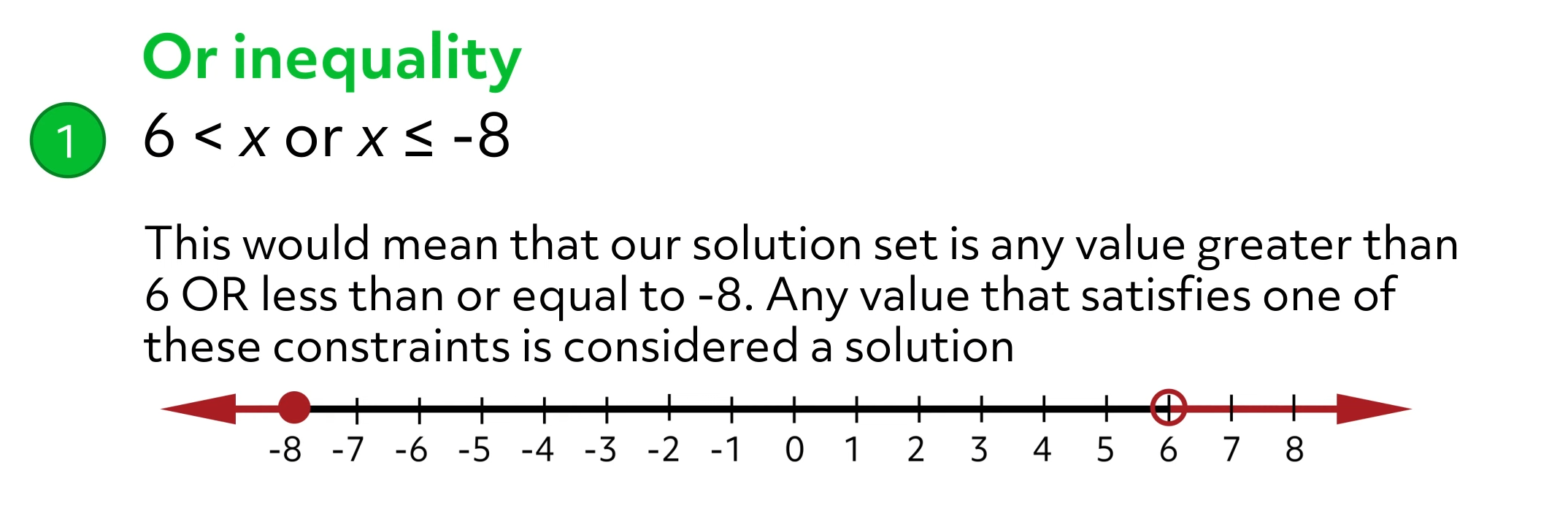
“And” Inequality
An example of an “and” compound inequality could be used to describe something like the years a person is in school. This would generally be between the ages of 5 and 25, and we can represent this scenario with the compound inequality \(5\leq x\leq 25\). This would be read as “x is greater than or equal to 5, AND x is less than or equal to 25.” In this case, our solution set has to satisfy both constraints.
Remember, compound inequalities can be represented as either an “or” statement or an “and” statement, and can incorporate the following symbols:
| \(\gt\) | Greater than |
| \(\lt\) | Less than |
| \(\geq\) | Greater than or equal to |
| \(\leq\) | Less than or equal to |
Compound Inequality Examples
Let’s look at some examples.
Example #1
Example of an “or” compound inequality: \(6\lt x\text{ or}\text{ }x\leq -8\)
This would mean that our solution set is any value greater than 6 or less than or equal to -8. Any value that satisfies one of these constraints is considered a solution.
Example #2
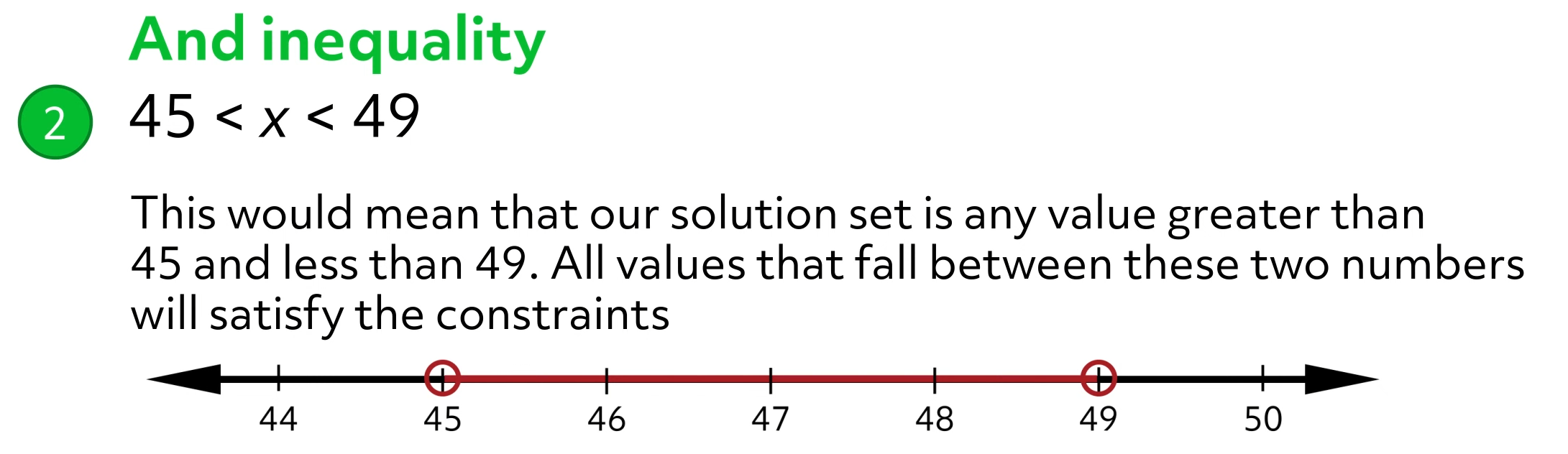
Example of an “and” compound inequality: \(45\lt x\lt 49\)
This would mean that our solution set is any value greater than 45 and less than 49. All values that fall between these two numbers will satisfy the constraints.
Solving Compound Inequalities
Now that we have an understanding of what a compound inequality is and what it represents, we can dive into the process for solving compound inequalities.
Example #1
Let’s solve for a compound inequality that is separated by an “or” for our first example.
Solve for \(>z\): \(5z+7\lt 27\text{ or}\text{ -}3z\geq 18\)
Our first step is to solve each constraint separately. The solving process is the same process for solving multi-step equations. The same rules apply, with one exception.
When you multiply or divide by a negative, the inequality will flip. We will see this process unfold as we finish this example.
So let’s start by solving this inequality.
We’ll start by subtracting 7 from both sides.
That will give us:
And then we divide by 5 on both sides.
So \(z>4\).
Now, let’s move to our other inequality.
For this, we just need to divide by -3 on both sides.
Remember, when we divide by a negative, our sign flips. So, instead of \(\geq\) , we’re going to have . \(\leq 18\text{ }\div \left ( -3 \right )=-6\).
So our final answer is:
This is now in a graphable form that can be represented on a line graph.
Now let’s check out a compound inequality that is separated by an “and.”
Solve for x: \(-12\lt 2-5x\leq 7\)
So for an “and” inequality like this, we can solve for x by doing inverse operations to all three parts. So, let me show you what I mean.
The first thing we want to do is subtract 2 to get x by itself. So we’re going to subtract 2 from this middle part here.
But if we subtract it from the middle part, we also need to do it to the left and right sides. So we’ll subtract 2 over here, and we’ll subtract 2 over here.
\(-12-2=-14\). The twos cancel out and we’re left with, \(-5x\). And \(7-2=5\).
Now, we’re going to do the same thing but divide by negative 5 on all three parts.
Remember, when we divide by a negative, we flip our inequality signs. So we’re going to have:
So our answer for this inequality is \(x\geq -1\text{ and}\text{ x}\lt \frac{14}{5}\).
Example #2
There are times when you will be working through the process of solving a compound inequality and your result will be no solution. What does this mean? What would this look like? Let’s take a look.
Solve for \(x\): \(5x-3\lt 12\text{ and}\text{ }4x+1\gt 25\)
So we’re going to start by solving each one of these inequalities separately.
So let’s start by adding 3 to both sides of this inequality.
This gives us:
And divide by 5 on both sides to get:
Now let’s move to this inequality over here:
We’re going to subtract 1 from both sides.
That gives us:
And then divide by 4 on both sides.
\(x\gt 6\)
So our solution is \(x\lt 3\) and \(x\gt 6\).
But wait, this is impossible. We are unable to find a value for \(x\) that is both less than 3, and greater than 6. If this occurs, the compound inequality is said to have “no solution.”
And that’s all there is to it. I hope that this video was helpful for you! Thanks for watching, and happy studying!
