
When it comes to functions and their graphs, one thing we may be interested in studying and looking for is asymptotes.
What is an Asymptote?
An asymptote is an invisible straight line that a function may get closer and closer to. For example, a vertical asymptote is where a function shoots straight up or down, and a horizontal asymptote happens when a function gets flatter and flatter over time. In this lesson, we are going to focus on horizontal asymptotes and discuss how to find them.
Horizontal Asymptotes
A horizontal asymptote is an “invisible” horizontal line that a function may get closer and closer to as \(x\) gets bigger and bigger.
Take a look at this graph.
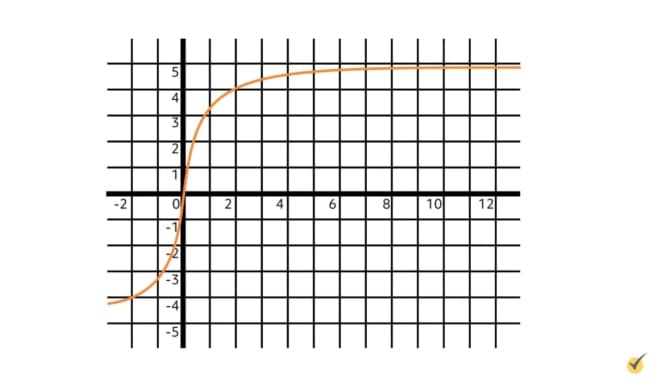
As we look at larger and larger \(x\)-values to the right, we can see that the function is flattening out and slowly getting closer and closer to a height of 5.
Notice that because it is flattening out like this, the function will actually never reach or cross \(y=5\). Even if we zoom out and look further and further right, the line will still not touch 5.
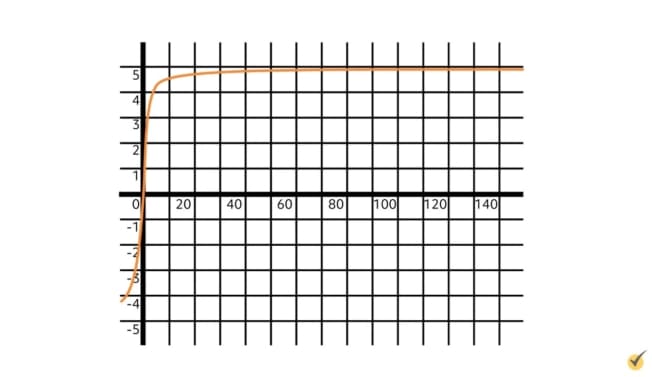
Because the function is getting ever closer and closer to 5, we say that this function has a horizontal asymptote along the line \(y=5\). Asymptotes are usually denoted with a dashed line, like this:
Identifying Horizontal Asymptotes with Graphs
Let’s look at some more graphs of functions and see if we can identify additional horizontal asymptotes.
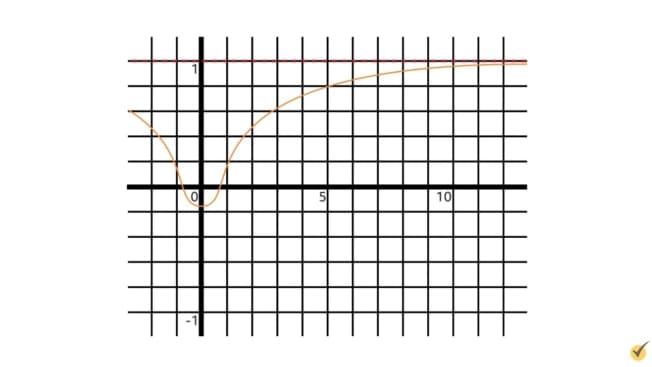
Example #1
This function tapers off around height 1 as we look further right, and since it never crosses or touches \(y=1\), we say that there is a horizontal asymptote at \(y=1\). Again, these are often shown graphically with a dashed line, so let’s add one in now.
Example #2
How about this function? Can you spot whether there is a horizontal asymptote?
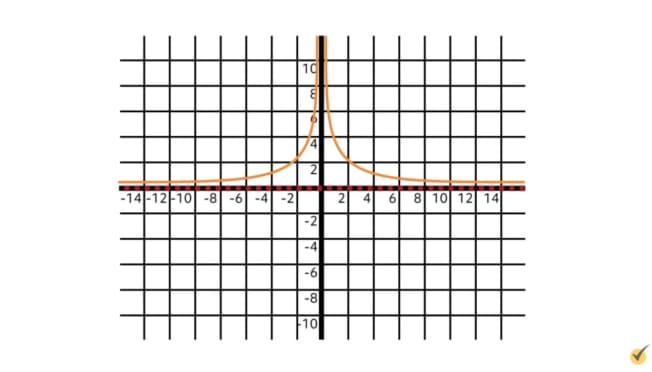
Here, we can see that as the function goes both further left and further right, it is approaching the \(x\)-axis, getting slowly closer and closer to it. While this function has the same horizontal asymptote on both the left and the right sides, keep in mind that a function can have an asymptote even if it is only on one side. Let’s draw the dashed line at \(y=0\) to denote the horizontal asymptote.
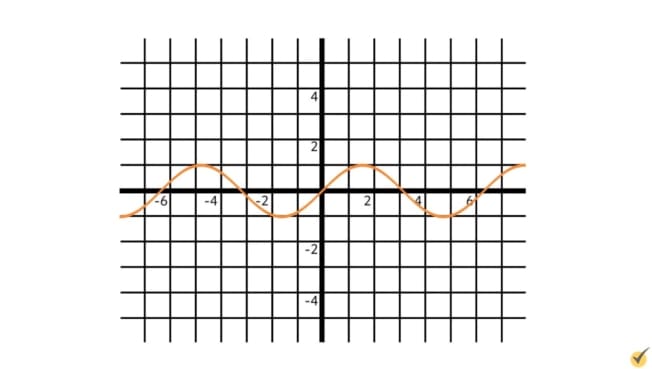
Example #3
Let’s look at one more. This is the graph of the function \(sin(x)\). Since it oscillates between positive and negative one infinitely, it will never “close in” on just one particular \(y\)-value. For this reason, \(sin(x)\) does not have any horizontal asymptotes.
Identifying Horizontal Asymptotes Without Graphs
Sometimes you’ll be asked to find asymptotes of functions without looking at pictures of their graphs. Fortunately, there is a way of identifying such asymptotes!
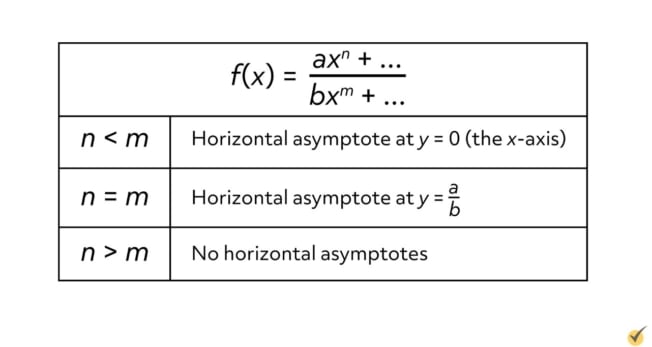
Horizontal asymptote problems usually incorporate functions written as big fractions, which can be generalized in this form
where \(ax^{n}\) is the term with the highest exponent in the numerator, and \(bx^{m}\) is the term in the denominator with the highest exponent.
If \(n\lt m\), or the highest exponent of the top is smaller than the highest exponent of the bottom, then the function will have a horizontal asymptote at the \(x\)-axis, or along \(y=0\).
If \(n\) and \(m\) are equal, or in other words, the numerator and denominator share the same highest power of \(x\), then the function will have a horizontal asymptote at the height of the coefficient a divided by coefficient \(b\).
If \(n\gt m\), or the highest power on the top is bigger than the highest power on the bottom, the function will not have any horizontal asymptotes.
As a first step for these kinds of problems, you’ll need to determine what is the highest power of \(x\) in the numerator, and what is the highest power of \(x\) in the denominator.
Example #1
Let’s try out an example. Find any horizontal asymptotes of the function \(f(x)=\frac{2x^{2}+4x+4}{x^{2}-9}\).
We need to determine which term has the highest power on top and which term has the highest power on the bottom. From the numerator we have \(2x^{2}\), and from the denominator we have \(x^{2}\). Since these are both to the same power (in this case, they are both squared), there will be a horizontal asymptote at the quotient of their coefficients, \(y=\frac{a}{b}\).
In this case, \(a=2\), and \(b=1\). \(2\div 1=2\), so there is a horizontal asymptote for this function at the line \(y=2\).
Example #2
Let’s try another problem. Find any horizontal asymptotes of the function \(g(x)=\frac{x^{2}+5}{4x+2}\).
What is the term with highest power in the numerator? \(x^{2}\). And what is the term with the highest power in the denominator? \(4x\), or \(4x^{1}\). Remember, for determining if horizontal asymptotes are present, we are first concerned with the exponents of these terms.
Since \(2\gt 1\), the numerator has a higher-powered term than the denominator, which tells us that there are no horizontal asymptotes for this function.
Example #3
Let’s look at one more example. Does the function \(f(x)=\frac{x^{2}+x+6}{x^{3}+4x^{2}+8}\) have any horizontal asymptotes? If so, where? Feel free to pause the video here and give it a shot yourself!
How did you do? Let’s compare. Just like in the previous examples, you must determine which term in the top has the highest power and which term in the bottom has the highest power. On the top, we have the term \(x^{2}\), and on the bottom we have \(x^{3}\).
Comparing their exponents, we see that \(2\lt 3\), which tells us that there should be a horizontal asymptote along the \(x\)-axis, \(y=0\).
To understand a real-life example of an asymptote, consider a piping hot cup of hot chocolate. If the cup is left out on the countertop, it will slowly cool down to a more pleasant temperature. It won’t get cooler than room temperature though, so as it gets closer to room temperature, its rate of cooling will slow down until eventually it matches room temperature and stays there.
Remember, horizontal asymptotes are usually pretty easy to spot graphically; just look for where a function “flattens out” at larger and larger \(x\)-values. They can also be found algebraically by comparing the powers of terms in the numerator and denominator of the function.
When the highest powers are equal, there is a horizontal asymptote at the line \(y=\frac{a}{b}\), the quotient of the coefficients. When the denominator has a higher power, there is a horizontal asymptote at the \(x\)-axis, and when the numerator has a higher power, there are no horizontal asymptotes.
I hope this video was helpful. Thanks for watching, and happy studying!
