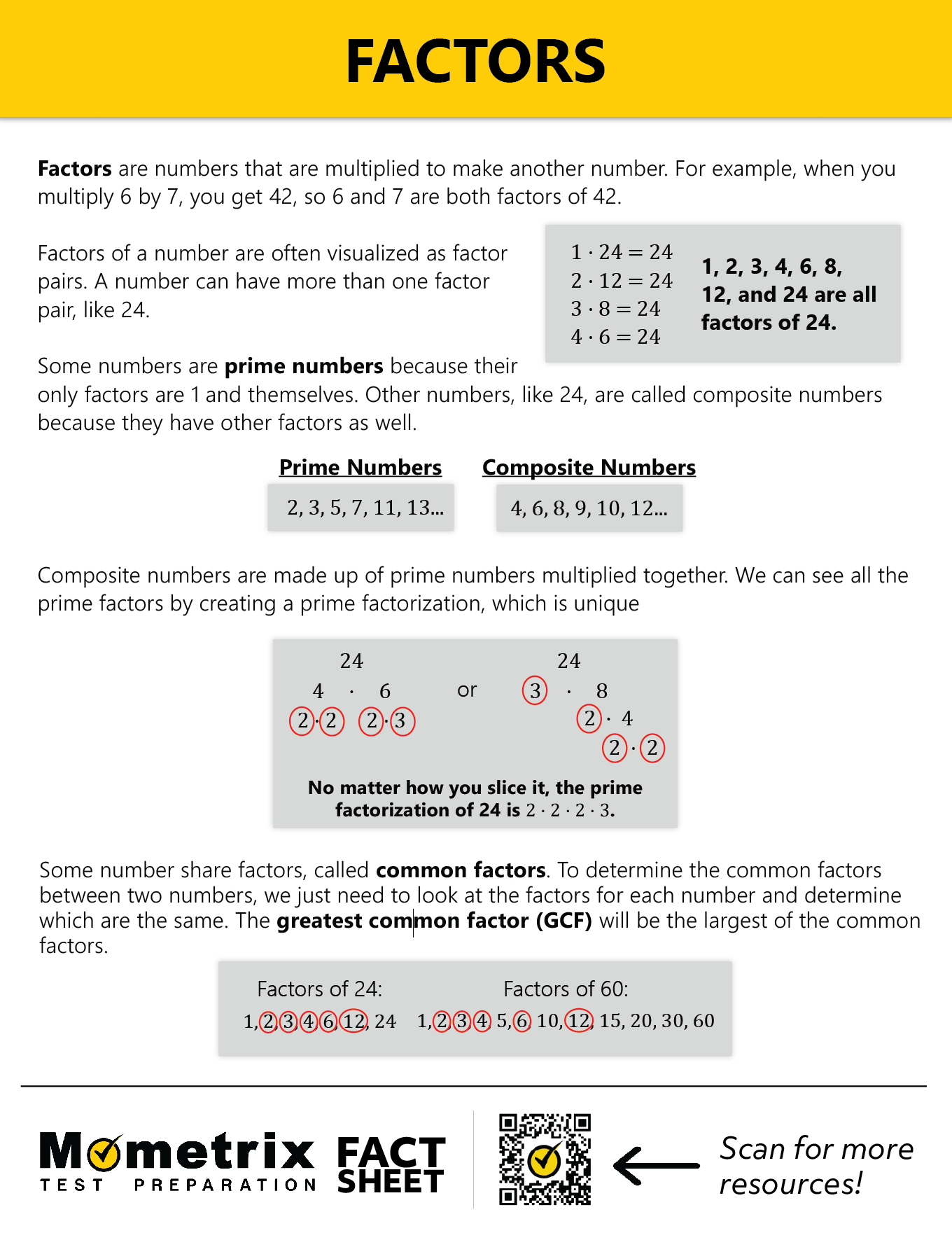
What is a Factor?
Factors in math refer to a number, or numbers, that produce a given number when multiplied. For example, when you multiply 6 by 7, you get 42. Well, 6 and 7 are the factors that contributed to the outcome of 42.
But those are not the only potential factors to getting 42. Like I said, factors refer to numbers that produce a given number when multiplied. So, any two numbers that I multiply together to get 42 are considered factors of 42. Let’s see what else we have:
\(2\times 21=42\)
\(3\times 14=42\)
\(6\times 7=42\)
Since all of these numbers (1, 2, 3, 6, 7, 14, 21, and 42) can be multiplied together to get 42, they are all considered factors of 42.
Another way that we could look at this is through division. Let’s say you are asked the question “Is 9 a factor of 45?” Well, to find out, you can divide 45 by 9, and determine whether or not the remainder is zero. In other words, is your answer a whole number? If you find a number with a 0 remainder, then both 9 and that number are factors of 45. Since we can see that after the division the remainder is zero, this tells us that the divisor (9) is a factor of the dividend (45). So, the answer to our question “Is 9 a factor of 45?” is yes!
Now, let’s take a look at another one. Is 8 a factor of 45? When we divide 45 by 8, the divisor we are left with is a remainder of 5. So, 8 is not a factor of 45. This means that there are not 8 equal parts to 45.
So, these are examples of what factors are, but there are also types of factors: common factors, greatest common factors, and prime factors. These are all exactly what they sound like.
Common Factors
Common factors are factors that two numbers share, or have in common. For example, let’s look at the factors of 35 and 40. For 35 we have: 1 and 35, because 1×35=35. We also have 5 and 7, because 5×7=35. That’s about it!
Let’s move over to 40. For 40 we have 1 and 40, because 40×1=40. We also have2×20, because when you multiply those you get 40. We also have 4×10 and 5×8, all of which end up equaling 40. Our factors for 40 are 1, 2, 4, 5, 8, 10, 20, and 40.
To determine the common factors between 35 and 40, we just need to look at each list of factors for each number and determine which ones are the same. So, in the case of 35 and 40, the only factors that they share between these two lists, are 1 and 5. So, 1 and 5 are the common factors.
Greatest Common Factor (GCF)
The next type of factor is a greatest common factor. This is the highest value common factor. You look at the list of common factors, like we have here, and determine which number is largest. In the case of 35 and 40, 1 and 5 are the only factors that they have in common, and 5 has a higher value than 1; therefore, 5 is the greatest common factor.
Prime Factor
Now, the last type of factor is a prime factor. A prime factor is any number that can only be divided by 1 and itself to produce a whole number. For example, 11 is a prime factor. Because it can only be divided by 1 and itself, when you multiply itself by 1, you end up with 11. There’s no other combination of factors that will result in 11.
I hope this lesson was helpful. Thanks so much for watching!
Frequently Asked Questions
Q
What is a factor?
A
A factor is any integer that can be multiplied by another integer to get the integer you are looking for. For example, 3 is a factor of 12 because 3 can be multiplied by 4 to get 12.
Q
What is the factor of any number?
A
The only number that is a factor of any number is 1 because 1 times any number is that number.
Q
Is 0 a factor of any number?
A
The only number 0 is a factor of is 0. This is because 0 times any number gives you 0, so it will never be able to be multiplied by a number and get any number other than 0.
What is a Factor? (PDF)
Factor Practice Questions
What are the factors of 64?
The correct answer is 1, 2, 4, 8, 16, 32, 64.
\(1×64=64\)
\(2×32=64\)
\(4×16=64\)
\(8×8=64\)
What are the common factors of 24 and 36?
The correct answer is 1, 2, 3, 4, 6, 12.
The factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
The factors that they both have in common: 1, 2, 3, 4, 6, 12
What is the Greatest Common Factor of 45 and 30?
The correct answer is 15.
The factors of 45: 1, 3, 5, 9, 15, 45
The factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
The greatest factor they have in common: 15
Which number is NOT a factor of 100?
The correct answer is 8. The factors of 100 are \(1×100\), \(2×50\), \(4×25\), \(5×20\) and \(10×10\).
Which number is a prime factor?
The correct answer is 7. The number 7 has only two factors, 1 and 7. When a number has only two factors (1 and itself) it is said to be prime.