
Hey guys! Welcome to this video on how to cross multiply fractions.
When cross multiplying fractions, the name sort of hints at how this is actually done.
You literally multiply across. Let’s say you have two fractions that are set equal to each other. So let’s say, \(\frac{a}{b}=\frac{c}{d}\).
Well, to cross multiply them, you multiply the numerator in the first fraction times the denominator in the second fraction, then you write that number down. Then you multiply the numerator of the second fraction times the number in the denominator of your first fraction, and you write that number down.
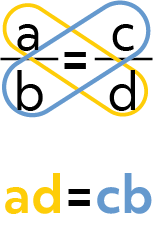
The reason we cross multiply fractions is to compare them. Cross multiplying fractions tells us if two fractions are equal or which one is greater. This is especially useful when you are working with larger fractions that you aren’t sure how to reduce.
How to Cross Multiply
Cross Multiply Fractions – Example 1
Find which of the two fractions is greatest.
\(\frac{4}{26}=\frac{7}{32}\)
So, when we cross multiply it, when we set it equal, and then cross multiply these two fractions together, we get 128. So \(4\times 32=128\). And when we cross multiply these two, we get \(7\times 26=182\). So, we know that \(\frac{7}{32}\) is greater than \(\frac{4}{26}\) because 182 is greater than 128.
We must always remember that the number that we multiplied with our numerator represents that corresponding fraction. So this number (128) is representing this fraction \((\frac{4}{26})\), and this number (182) is representing this fraction \((\frac{7}{32})\). I mention this, because it may be a little confusing to see numbers taken from two different fractions being multiplied together, but the product only representing one of the fractions and not the other. 128 goes on the left side to represent \(\frac{4}{26}\) and \(7\times 26=182\) goes on the right side to represent this fraction right here \((\frac{7}{32})\).
Cross multiplying fractions helps us to see if numbers are equal, and if not, which is bigger and which is smaller. But that is not its only use. Cross multiplying fractions can help us to solve for unknown variables in fractions.
Cross Multiply Fractions – Example 2
Let’s say we have two fractions \(\frac{9}{16}=\frac{x}{27}\). We can cross multiply anytime we have a fraction that is set equal to another fraction. Now, to cross multiply we do the exact same thing that we did in our last example. We take the numerator of one side and multiply it times the denominator of the other side, and do this same the from the numerator of the other side. In this case, we multiply \(9\times 27\) and \(16\times x\). This would give us \(243=16x\). Now, all we have to do to get x by itself is divide both sides by 16. This cancels out, and this gives us \(x=\frac{243}{16}\), and you can simplify this even further. Now, we would do this exact same thing even if \(x\) is in our denominator, it doesn’t matter.
I hope that this video over cross multiplying fractions has been helpful to you.
See you guys next time!
Frequently Asked Questions
Q
How do you cross multiply fractions?
A
Cross multiply fractions by multiplying the denominator of one fraction with the numerator of the other fraction and then comparing the two values. The fraction with the larger value is the larger fraction.
Be careful to always go from denominator to numerator! If you go numerator to denominator, you will get the wrong fraction as the one that is greater.
Example: Which fraction is greater: \(\frac{4}{5}\) or \(\frac{3}{8}\)?
Therefore, \(\frac{4}{5}\) is greater than \(\frac{3}{8}\).
Q
When do you cross multiply fractions?
A
Cross multiply fractions when you want to determine if one fraction is greater than another, or if you are looking for a missing numerator or denominator in equivalent fractions.
Q
How do you cross multiply fractions with different denominators?
A
Almost all fractions being cross multiplied will have different denominators. This does not affect the process at all. Cross multiply as normal.
Q
Why does cross multiplying fractions work?
A
Cross multiplying fractions to determine if one is greater than the other works because it is a shortcut for converting the fractions to a common denominator and comparing fractions.
Example: Which is greater: \(\frac{7}{9}\) or \(\frac{8}{12}\)?
Let’s solve this using cross multiplication.
This tells us that \(\frac{7}{9}\)>\(\frac{8}{12}\)
Now, let’s solve this by converting and comparing.
\(\frac{7}{9}×\frac{12}{12}=\frac{84}{108}\)
\(\frac{8}{12}×\frac{9}{9}=\frac{72}{108}\)
This tells us that \(\frac{7}{9}>\frac{8}{12}\).
Cross multiplying fractions to find a missing numerator or denominator for equivalent fractions works because it is a shortcut for rearranging to isolate the variable.
Example: Solve for \(x\): \(\frac{3}{7}=\frac{2}{x}\)
Let’s solve this using cross multiplication.
\(\frac{3}{7}=\frac{2}{x}\)
\(3x=14\)
\(x=\)\(\frac{14}{3}\)
Now, let’s solve this by rearranging.
\(\frac{3}{7}=\frac{2}{x}\)
\(\frac{3}{7}\)\(x=2\)
\(x=2×\)\(\frac{7}{3}\)
\(x=\)\(\frac{14}{3}\)
Q
Can you cross multiply when adding fractions?
A
No, you cannot cross multiply when adding fractions. Cross multiply only when you need to determine if one fraction is greater than another, or if you are trying to find a missing numerator or denominator in equivalent fractions.
Q
How do you cross multiply fractions with variables?
A
Cross multiply fractions with variables by multiplying opposite numerators and denominators of equivalent fractions, setting the values equal to one another, and solving for the variable.
Example: \(\frac{4}{5}=\frac{x}{20}\)
\(4×20=5x\)
\(80=5x\)
\(16=x\)
Cross Multiplying Fractions Practice Questions
Which fraction is larger: \(\frac{17}{29}\) or \(\frac{12}{15}\)?
The fraction \(\frac{12}{15}\) is larger than \(\frac{17}{29}\). Cross multiplication can be used to answer this question.
First, multiply 17 by 15.
\(17\times15=255\)
Write 255 above \(\frac{17}{29}\), like this:
Next, multiply 29 by 12. \(29\times12=348\), so write 348 above \(\frac{12}{15}\), like this:
348 is larger than 255, so \(\frac{12}{15}\) is larger than \(\frac{17}{29}\).
Which of the following expressions is correct?
Cross multiplying each fraction pair results in this:
Therefore, \(\frac{3}{8}\)<\(\frac{4}{7}\) is the only correct expression.
Solve for the missing variable.
\(\frac{18}{21}=\frac{x}{63}\)
The correct answer is \(x=54\). To solve this problem, start by cross multiplying.
\(18\times63=21x\)
\(1,134=21x\)
Then, divide by 21 on both sides.
\(54=x\)
Solve for the missing variable.
\(\frac{7}{y}=\frac{42}{72}\)
The correct answer is \(y=12\). To solve this problem, start by cross multiplying.
\(7\times72=42y\)
\(504=42y\)
Then, divide by 42 on both sides.
\(12=y\)
A man has a garden that is 6 feet wide and 9 feet long. He is planning on increasing the width to 9 feet. If he wants to increase the length proportionally, what would be the new length?
To solve this problem, first set up proportional fractions.
\(\frac{\text{length}}{\text{width}}=\frac{6}{9}=\frac{9}{l}\)
Then, cross multiply to solve for \(l\).
\(9\times9=6l\)
\(81=6l\)
\(13.5=l\)
The new garden will be 13.5 feet long.







