How to Find the Y-Intercept
There is more than one way to find the \(y\)-intercept, depending on your starting information. Below are three ways to identify the \(y\)-intercept on a graph, in a table, or with an equation:
1. Find the \(y\)-intercept of a linear function using the slope and a given point.
First, identify the slope and a point on the graph. Once this is done, write a linear equation in slope-intercept form (\(y = mx + b\)). Using the given point (\(x,y\)) and the slope \(m\), rewrite the equation by substituting the appropriate values for \(x\), \(y\), and \(m\). Given this information, solve the equation for \(b\) to identify the \(y\)-intercept.
Example: Consider a graph containing the point \((-2,5)\) where the slope is 3.
Start by writing a linear equation in slope-intercept form.
Next, replace variables \(y\), \(m\), and \(x\) with their corresponding values.
From here, solve the one-step equation for \(b\).
Because \(b=11\), the \(y\)-intercept is 11.
2. Find the \(y\)-intercept of a linear function using two points from a table or graph.
Using a table or a graph, identify two points shown. First, record the coordinates (\(x,y\)) for each point. Using this information, find the rise and run to identify the slope. Calculate the rise by finding the difference in the \(y\)-coordinates of the two points. Calculate the run by finding the difference in the \(x\)-coordinates of these two points. Divide the difference in \(y\)-coordinates by the difference in \(x\)-coordinates to find the slope.
Once the slope has been identified, write a linear equation in slope-intercept form (\(y = mx + b\)). Using one set of coordinates (\(x,y\)) and the slope \(m\), rewrite the equation by substituting the appropriate values for \(x\), \(y\), and \(m\). Then, solve the equation for \(b\) to identify the \(y\)-intercept.
Example: Consider a graph containing the points \((3,6)\) and \((-1,-2)\). Find the \(y\)-intercept.
Start by calculating the rise and run to find the slope. The difference in \(y\)-coordinates is 8 and the difference in \(x\)-coordinates is 4. \(8 ÷ 4 = 2\), so the slope = 2.
Next, write an equation in slope-intercept form.
Next, replace variables \(y\), \(m\), and \(x\) with their corresponding values. Choose one point given to substitute for \(x\) and \(y\).
From here, solve the one-step equation for \(b\).
Because \(b=0\), the \(y\)-intercept is 0.
3. Find the \(y\)-intercept of a linear function using an equation.
If you already have the equation of the line, solve algebraically to find the \(y\)-intercept. Since the \(y\)-intercept always has a corresponding \(x\)-value of 0, replace \(x\) with 0 in the equation and solve.
Example: Find the \(y\)-intercept of the line \(3x+(-2y)=12\).
First, rewrite the equation by substituting 0 for \(x\).
Next, solve the one-step equation for \(y\).
Because \(y=-6\), the \(y\)-intercept is -6.
Finding the Y-Intercept in a Quadratic Function
In a quadratic function, the \(y\)-intercept is the point at which the parabola crosses the \(y\)-axis. In the graph shown, the \(y\)-intercept is -3.
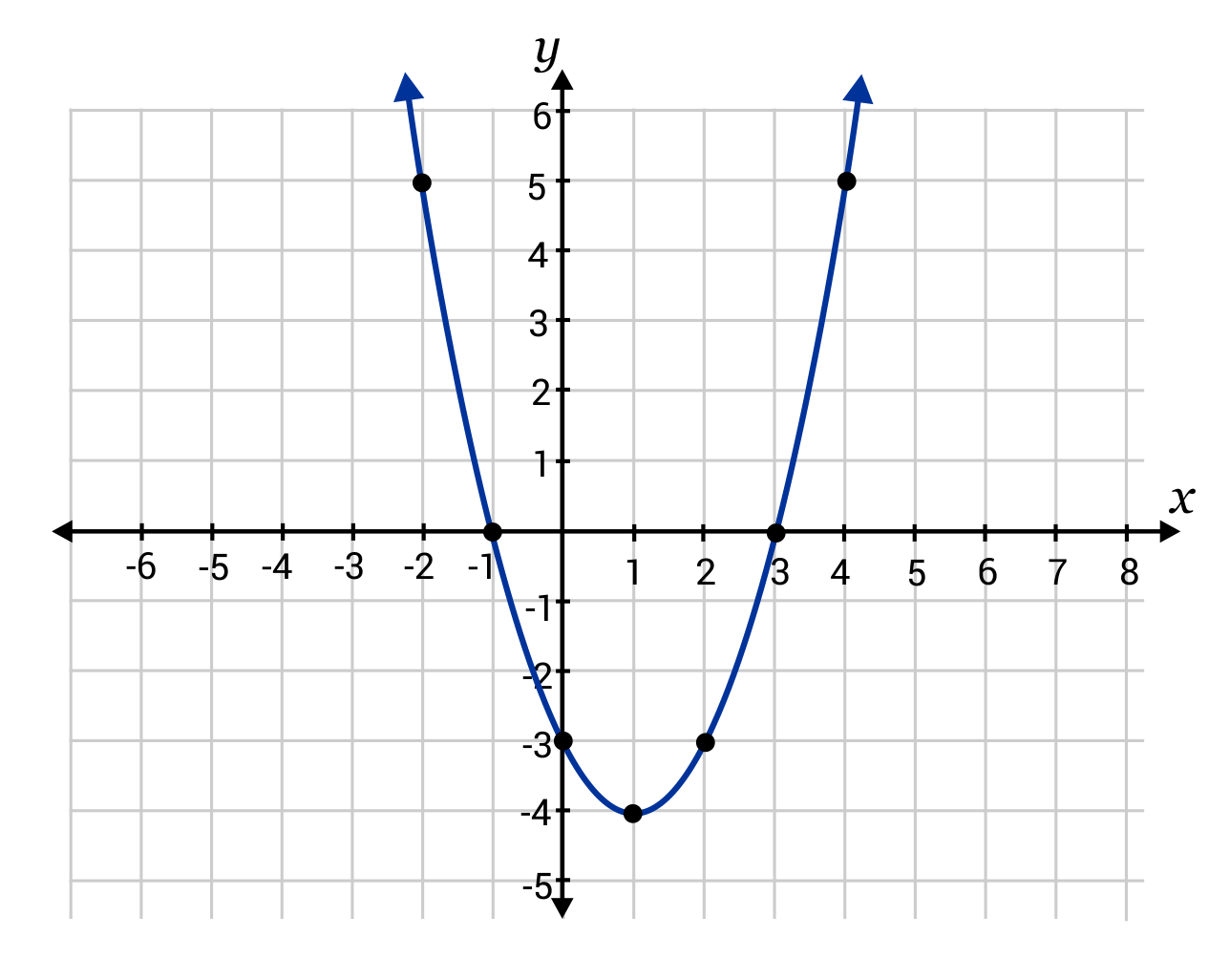
The standard form of a quadratic equation is written as \(y=ax^2+bx+c\), where \(x\) and \(y\) are variables and \(a\), \(b\), and \(c\) are known constants.
To find the \(y\)-intercept from a quadratic equation, substitute 0 as the value for \(x\) and solve. The \(y\)-intercept is always equal to the value of \(c\) in the equation.
Example: Find the \(y\)-intercept in the quadratic equation \(y=2x^2+3x+4\).
First, rewrite the equation by substituting 0 for \(x\).
Next, solve the one-step equation for \(y\).
Because \(y=4\), the \(y\)-intercept is 4.
FAQs
Q
How do you find the \(y\)-intercept?
A
There is more than one way to find the \(y\)-intercept, depending on your starting information. If the linear equation is given, solve algebraically to find the \(y\)-intercept. Since the \(y\)-intercept always has a corresponding \(x\)-value of \(0\), replace \(x\) with \(0\) in the equation and solve for \(y\).
On a graph, the \(y\)-intercept can be found by finding the value of \(y\) when \(x=0\). This is the point at which the graph crosses through the \(y\)-axis.
Q
What is the \(y\)-intercept of an equation?
A
When the equation of a line is written in slope-intercept form \((y=mx+b)\), the \(y\)-intercept is the constant, which is represented by the variable \(b\). For example, in the linear equation \(y=4x-5\), the \(y\)-intercept is \(-5\).
Q
Where is the \(y\)-intercept on a graph?
A
The \(y\)-intercept is the point where the graph of a line crosses the \(y\)-axis. In the coordinate plane shown, the \(y\)-intercept is \(4\) because the graph passes through \(4\) on the \(y\)-axis.
Q
Why is the \(y\)-intercept important?
A
The \(y\)-intercept is important because it tells the value of \(y\) when \(x=0\). It provides a starting point for a linear function.
Q
How do I find slope and \(y\)-intercept?
A
On a graph, the \(y\)-intercept is the point where the line intersects the \(y\)-axis. The corresponding \(x\)-coordinate is always \(0\). The slope is found by calculating rise over run. This is done by finding the difference in the \(y\)-coordinates and \(x\)-coordinates and dividing these differences.
When a linear equation is written in slope-intercept form \((y=mx+b)\), the slope is represented by the variable \(m\). It is the coefficient to \(x\) in the equation. The \(y\)-intercept is the constant, represented by the variable \(b\).
Q
Is \(b\) the \(y\)-intercept?
A
When a linear equation is written in slope-intercept form \((y=mx+b)\), the \(y\)-intercept is represented by the constant variable \(b\). For example, in the equation \(y=6x+8\), the variable \(b\) corresponds with \(8\). This is the \(y\)-intercept.
Q
What does the \(y\)-intercept mean in real life?
A
The \(y\)-intercept is the \(y\)-value that corresponds to \(x\) when \(x=0\). In real life, this often refers to the starting point when something is being measured.
For instance, consider population change in the United States. In this scenario, the \(x\)-values could represent time, measured in years. The \(y\)-values could represent the population, measured in millions of people. When \(x=0\), this value represents the starting year for measuring population change. The corresponding \(y\)-value represents the size of the population in the starting year. This value is the \(y\)-intercept.
Practice Questions
The function \(y=\frac{1}{2}x+3\) is graphed below. Use the graph to identify the y-intercept.
The correct answer is A. The y-intercept is the point where the graph crosses the y-axis. When studying the graph above, notice that the line crosses the y-axis at (0, 3), so 3 is the y-intercept.
Which variable represents the y-intercept for a quadratic equation in standard form:
\(y = ax^2+bx+c\)
The correct answer is C. In a quadratic equation, the variable \(c\) represents the \(y\)-intercept. This is the point where the graph intersects the \(y\)-axis.
Without graphing, identify the \(y\)-intercept for the function \(y=-4x+\frac{1}{2}\)
The correct answer is D. When a function is in slope-intercept form, the y -intercept can quickly be identified because it is represented by the variable b. In this example, b is \(\frac{1}{2}\), therefore the y-intercept is \(\frac{1}{2}\).
The quadratic equation \(y=-3x^2-3x+1\) is graphed below. What is the \(y\)-intercept?
The correct answer is B. The \(y\)-intercept is the point where the graph crosses the \(y\)-axis. When studying the graph above, notice that the line crosses the \(y\)-axis at 1, so 1 is the \(y\)-intercept.
Which equation is represented by the graph below? Use your understanding of \(y\)-intercept to determine your answer.
The correct answer is B. The quadratic equation \(y=2x^2-3x+4\) is written in standard form. This makes it easier to identify the \(y\)-intercept, because \(c\) always represents the \(y\)-intercept. The graph shows a quadratic equation that intersects the \(y\)-axis at 4, and the only equation where \(c\) is equal to 4 is Choice B.




