
Hi, and welcome to this overview of quadratic equations! Before we dive into how to solve them, let’s first talk about quadratic functions.
Quadratic Functions
When we graph quadratic functions, we’ll notice that they can be used to tell all kinds of visual stories, from a daredevil shooting out of a cannon to a satellite dish listening to interstellar signals.
Equations for these functions generally look like this: \(f(x)=ax^2+bx+c\) and their graphs form a characteristic shape called a parabola, which looks something like this one:
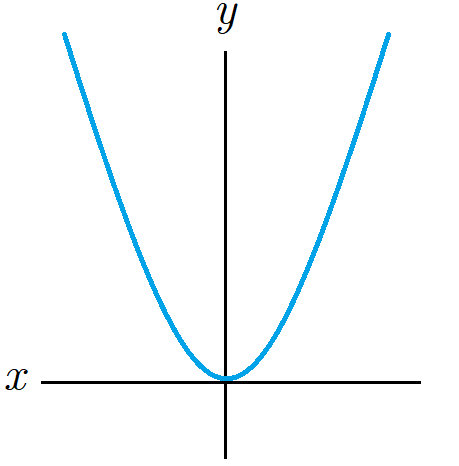
The different characteristics of quadratic functions that are most commonly analyzed are the vertex (the maximum or minimum point), the x-intercepts (the zeros), and the axis of symmetry.
Now that we have a little background, let’s dive further into solving quadratic equations and interpreting the results.
Solving Quadratic Equations Example
So what do we mean by “solving”? In this case, one of the things it means is to figure out which values of the variable, if any, make the equation 0. So instead of the function \(f(x)=ax^2+bx+c\), we write the related equation: \(0=ax^2+bx+c\).
In other words, the solutions to a quadratic equation are the values that make the quadratic function true when \(f(x)=0\) or \(y=0\).
This is the function \(f(x)=-x^{2}+2x+8\):
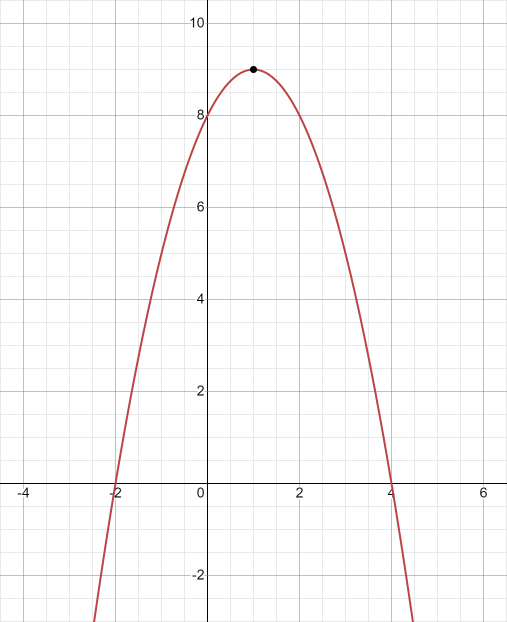
Every point on the graph satisfies this equation.
Solving \(0=-x^{2}+2x+8\) gives us two solutions because the function equals 0 only when it crosses the \(x\)-axis.
Here’s another way to look at it. To solve a quadratic equation means to find the \(x\)-intercepts of the related function, also known as the zeros.
Standard Form
Before you get started with any solving method, make sure your equation is written in standard form: \(ax^2+bx+c=0\). This will prevent errors and can provide insight into choosing the most appropriate method for solving an equation.
If your equation is not in standard form, simply add or subtract terms as needed.
For instance, \(2x+8=x^{2}\) is not written in standard form, but by subtracting \(x^{2}\) from both sides, we get \(-x^{2}+2x+8=0\), which is now in standard form.
Graphing
The first method we’ll look at is graphing. If you have access to a graph or can easily create one using the internet or a graphing calculator, this can be a great method to use. Let’s look at an example. Here is the graph of \(f(x)=-x^{2}+2x+8\).

The solutions to the equation \(-x^{2}+2x+8=0\) are \(x = -2\) and \(x = 4\). Solutions can always be verified by plugging them back in to the original equation:
\(-(-2)2 + 2(-2) + 8 = 0\)
\(-4 – 4 = 0\)
\(0 = 0\)
\(-(4)2 + 2(4) + 8 = 0\)
\(-16 + 8 + 8 =0\)
\(0 = 0\)
Sometimes, quadratic equations can be simplified and solved by factoring.
Looking at our sample equation, we have \(-x^{2}+2x+8=0\).
The left side can be factored into \((-x+4)(x+2)=0\).
Zero Product Property
Now let’s pause. There’s a property called the zero product property that says that if there are two numbers whose product is 0, one of the numbers must be 0. In more mathematical terms: If \(a\) and \(b\) are real numbers and \(ab=0\), then \(a=0\) or \(b=0\).
Makes sense, right? Back to our equation, \((-x+4)(x+2)=0\).
This means that \(-x+4=0\) or \(x+2=0\). So we solve both!
We’re going to subtract 4 from both sides, which gives us \(-x=-4\). Then divide by -1 to get \(x=4\).
For this equation, we subtract 2 from both sides, and we’re left with \(x=-2\).
So our zeroes are \(x=4\) and \(x=-2\).
These match what we found on our graph.
Completing the Square Method
Factoring is nice, but not every equation can be factored easily. Luckily, there are a couple more methods we can use, including the completing the square method.
The idea behind this method is to create a quadratic equation that contains a perfect square and then take the square root to find the solutions.
Here’s our equation again: \(-x^{2}+2x+8=0\). To complete the square, the equation needs to not only be in standard form, but the coefficient on the squared term needs to be positive instead of negative. So, we divide all terms by -1 to get ready. This gives us \(x^{2}-2x-8=0\).
First, move the constant term to the other side by itself. For this, we’ll add 8 to both sides. This gives us \(x^{2}-2x=8\).
Now we need to add a number that creates a perfect square on the left-hand side. Let’s consider some perfect squares:
| Factored Form | Expanded Form |
|---|---|
| \((x+2)^2\) | \(x^2+\) \(4\) \(x\) \(+\) \(4\) |
| \((x-3)^2\) | \(x^2-\) \(6\) \(x\) \(+\) \(9\) |
| \((x+4)^2\) | \(x^2+\) \(8\) \(x\) \(+\) \(16\) |
To complete the square in our equation, we’ll add a number to both sides of our equation. In the examples, notice that number is \((\frac{b}{2})^{2}\).
\(9=(\frac{-6}{2})^{2}\)
and
\(16=(\frac{8}{2})^{2}\)
In our equation, we’ll add \((\frac{-2}{2})^{2}=1\), since our \(b = -2\). Remember, an equation only stays equal if you change both sides in the same way, so since we’re gonna add 1 to our left side, we also need to be sure to add 1 to the right side: \(x^{2} – 2x + 1 =9\).
Now the left side can be factored: \((x-1)^{2}=9\)
Since we have a perfect square, we take the square root of both sides. On the right-hand side, we need to account for both positive and negative square roots.
\(x-1=±3\)
Now, we’ll split into separate mini-equations: \(x-1=3\) and \(x-1=-3\). We’re going to solve for \(x\) over here (\(x-1=3\)) by adding 1 to both sides, which gives us \(x=4\). And here (\(x-1=-3\)) we’re going to do the same; add 1 to both sides, which gives us \(x=-2\).
We get the same solutions as before.
Completing the square can be used with any quadratic equation, but if you start with a perfect square and don’t realize it, the equation will look the same after you use this method as it did when you started.
The Quadratic Formula
There is one last method for us to examine. The quadratic formula, as you’ll see, involves the most algebra, but it has two distinct characteristics:
- It can truly be used with any quadratic equation.
- Part of it can be used to determine how many solutions to expect beforehand.
Here it is in all its glory: \(x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\)
The piece of the quadratic formula under the radical, the square root sign, is called the discriminant. Calculating its value helps us know how many solutions to expect.
Let’s take a minute to consider how many times a quadratic function can possibly intersect the \(x\)-axis:
| This example shows twice |
 |
| Sometimes, it’s only the vertex |
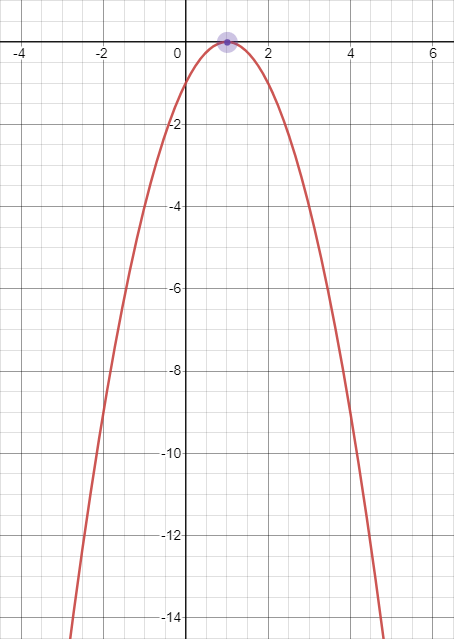 |
| Sometimes, it doesn’t intersect |
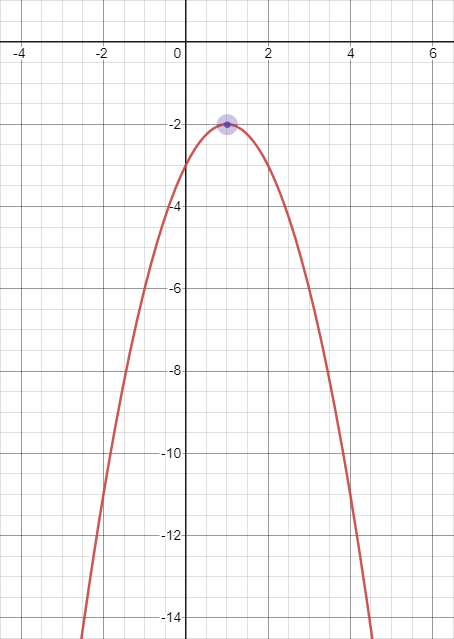 |
Because of the shape, these are our only choices. In order for a graph like this to intersect the \(x\)-axis more than two times, it would need to change direction again and thus, no longer be a parabola.
Now let’s consider square roots in general. If the square root of a number is greater than 0, there are two real solutions; taking the square root of a positive number yields positive and negative roots. If the square root is 0, there’s one real solution: 0. Taking \(\sqrt{0}=0\). If the square root of a number is less than 0, there are zero real solutions. We can’t take the square root of a negative number and end up with a real number.
| If \(\sqrt{\text{number > }0}\) | If \(\sqrt{0}\) | If \(\sqrt{\text{number < }0}\) |
|---|---|---|
| 2 real solutions | 1 real solution = 0 | 0 real solutions |
| Taking the square root of a positive number yields ± roots | Taking the square root of 0 is 0 | Taking the square of a negative number does not result in a real number |
So what does this have to do with the discriminant?
- If \(b^{2}-4ac\) > \(0\), then there are two real solutions (two \(x\)-intercepts).
- 2. If \(b^{2}-4ac=0\), there is one real solution (the vertex of the parabola is the \(x\)-intercept).
- And if \(b^{2}-4ac\) < \(0\), there are no real solutions (no \(x\)-intercepts).
Using our ongoing example, \(-x^{2}+2x+8=0\): \(a = -1\), \( b = 2\), and \(c = 8\).
The discriminant, \(D\), is \(b^{2}-4ac\), which is:
\(=4+32\)
\(=36\)
Since \(36\) > \(0\), we know that there are two real solutions to our equation, as expected.
What’s the point of calculating the discriminant? If you get in the habit of checking it every time, a few things happen:
- If there are no solutions to your equation, you’ll know right away and can stop
- If there are one or two solutions, the discriminant will serve as a check, regardless of the method used
- If you use the quadratic formula, a chunk of it is already calculated
Speaking of the quadratic formula, let’s try it out!
Again, \(a = -1\), \( b = 2\), and \(c = 8\). Plus, we already know the discriminant. So we have \(-b\), which is \(-2\pm \sqrt{\text{discriminant}}\), which we found was 36 (so \(\sqrt{36}\)) all over \(2a\), which is -1: \(\frac{-2\pm \sqrt{36}}{2(-1)}\).
This is equal to \(\frac{-2\pm 6}{-2}\).
Now we’re going to split it into two equations. We have \(\frac{-2+ 6}{-2}\) and then \(\frac{-2- 6}{-2}\).
\(\frac{-2- 6}{-2}\) gives us \(\frac{-2- 6}{-2}=\frac{-8}{-2}=4\).
So \(x=-2\) and \(x=4\).
We’ve seen all four quadratic equation solving methods in action. Now let’s put some context around our practice equation.
Suppose our function \(f(x)-x^{2}+2x+8\) represents the height of a rock from the ground (in meters) you throw off of a small cliff as a function of time (in seconds). We want to know how long it takes for the rock to hit the ground.
In order to do that, we would solve the equation \(-x^{2} +2x + 8 = 0\), which we have already done many times over. Remember, the 0 represents 0 height. In function terms, this means “on the \(x\)-axis.” In this situation, that means “on the ground.”
We know our mathematical solutions are \(x=-2\) and \(x=4\). In this situation, the solution of -2 doesn’t make sense. What does it mean? 2 seconds ago? Travel back in time 2 seconds? We would state that the rock landed after 4 seconds.
I hope this video helped you understand quadratic equations and how they work! Thanks for watching, and happy studying!
Quadratic Equation Practice Questions
What is the solution to the quadratic equation \(x^2+7x+15=5\)
The first step to solving a quadratic equation is to set the function equal to zero. We can subtract 5 from both sides to make the equation \(x^2+7x+10=0\). Once it is in this form, we should always check the discriminant, \(b^2-4ac\), to determine the number of real solutions to the quadratic equation, which is two in this case because \(7^2-4(1)(10)=9\), which is greater than zero. The second step is to see if we can solve this by factoring. We look at 10 and ask ourselves, what are the factors of 10? The factors of 10 are 5 and 2, and 10 and 1. It is easy to see that the combination of 5 and 2 add to 7, which is the coefficient of our middle term. The factored form of this equation is \((x+2)(x+5)=0\). We can use the Zero Product Property to set each factor equal to zero and solve for x which gives us \(x=-2\) and \(x=-5\).
Which equation shows the quadratic equation \(x^2-18x+8=-9\) after completing the square?
We must first check the discriminant, \(b^2-4ac\), to see if there are any solutions and the number of solutions to the quadratic equation. First, we will set the equation equal to zero by adding 9 to both sides to get \(x^2-18x+17=0\). The discriminant is \((-18)^2-4(1)(17)=256\), which is greater than zero, therefore, this quadratic equation has two real solutions. When solving a quadratic equation using the completing the square method, the first step is to move all the constants to the right side of the equation, \(x^2-18x=-17\). Then, we take the coefficient of x and divide it by two and square it, \((\frac{-18}{2})^2=81\), which becomes the third term in our quadratic equation, but you must add it to both sides to maintain the equality of the equation and get \(x^2-18x+81=-17+81\). Simplify the equation \(x^2-18x+81=64\). Then we will factor the quadratic equation \((x-9)(x-9)=64\), which can be written as \((x-9)²=64\).
What is the solution to the quadratic equation \(-8x^2-3x+22=0\)?
We will start by checking the discriminant, \(b^2-4ac\), to determine the number of solutions for the quadratic equation, which is \((-3)^2-4(-8)(22)=713\), therefore, there are two real solutions. Since there is a leading coefficient that does not divide equally into the other terms we will use the quadratic formula, \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\), to solve the equation. We will start by substituting the values into the formula \(x=\frac{-(-3)\pm\sqrt{(-3)^2-4(-8)(22)}}{2(-8)}\). Simplify the equation \(x=\frac{3\pm\sqrt{713}}{-16}\) then solve for each value \(x=-1.856\) and \(x=1.481\).
Smith throws a ball into the air. The height of the ball, h, in feet above the ground after t seconds can be shown using the function \(h(t)=-2x^2+7x+12\). How many seconds is the ball in the air?
To find the number of seconds the ball is in the air we will solve for t using the quadratic formula, \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\). We will begin by substituting the values for a, b and c into the formula, \(x=\frac{-7\pm\sqrt{(7)^2-4(-2)(12)}}{2(-2)}\). Simplify the equation \(x=\frac{-7\pm\sqrt{145}}{-4}\), then solve for each, which is \(x=-1.26\) and \(x=4.76\). Since the question is asking for the number of seconds and we cannot have a negative number of seconds, we can conclude that the solution is only \(x=4.76\) seconds.
What is the total number of real solutions for the quadratic equation \(9x^2+12x+4=0\)?
To determine the number of real solutions, we use the discriminant, \(b^2-4ac\), which simplifies to 0 because \((12)^2-4(9)(4)=144-144=0\). Therefore, there is one real solution to this quadratic equation.
