Perimeter is defined as the total distance around a two-dimensional shape. The ability to calculate perimeter is a convenient skill to have because there are many real-world applications. For example, perimeter is used for calculating the boundary of a soccer field, the total amount of wood needed to create a picture frame, or the amount of materials needed to fence a backyard.
The perimeter of any polygon can be found by simply finding the sum of all of the side lengths. This is true regardless of how many sides the shape has, or how irregular the shape appears. Many polygons have perimeter formulas that can save a bit of time when calculating the sum of all side lengths. For example, the perimeter formula for a rectangle is \(P=2l+2w\), where the length and width are multiplied by 2, and then added together.
Similarly, the perimeter formula for a square is \(P=4s\), where s represents each side length. The perimeter formula for a circle, also known as the circumference, is calculated as \(C=2r\), where \(r\) represents radius, and can be approximated as \(3.14\). These formulas will generally save you time when calculating perimeter.
Having a strong foundational understanding of perimeter will also be relevant in more advanced math topics such as surface area calculations for three-dimensional solids. For example, in order to calculate the surface area of a cylinder \((SA=2rh)\), you need to know the perimeter of the circular base of that cylinder (\(2r\)). Perimeter calculations are embedded into many areas of math, so it is very useful to have a solid understanding of the topic.
It is common for perimeter problems to provide a shape with a few dimensions provided, and other dimensions unknown. For example, in the shape below, only four out of the six dimensions are provided. These kinds of perimeter problems are a bit more involved, but the ultimate goal is again to determine the total distance around the shape. Before calculating the perimeter, we need to identify the length of the missing side lengths. This can be done by comparing side lengths that are opposite of each other.
For example, the height of the rectangle below is \(12\text{ mm}\), therefore the missing side length on the right side of the figure needs to be \(5\text{ mm}\) so that both heights are equal \((12\text{ mm}=7\text{ mm}+5\text{ mm})\). The total width of the figure can be determined by adding the two partial widths \(15\text{ mm}+8\text{ mm}\), which equals \(23\text{ mm}\). Now that all side lengths are accounted for, the total perimeter can be calculated. When all side lengths are added, the result is \(70\text{ mm}\).
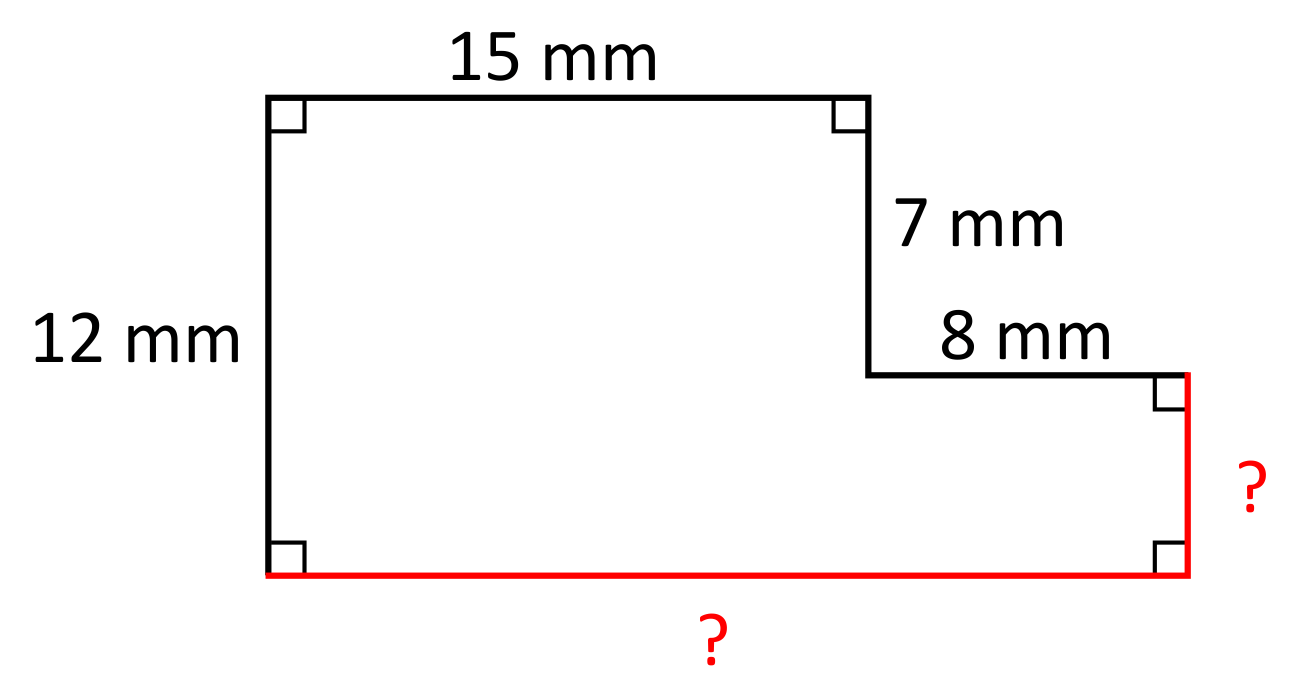
Another approach for finding the perimeter of rectangles with “pushed-in” corners is to visualize the “pushed-in” corner as being “pushed-out” to form a rectangle. When the corner is “pushed-out”, the perimeter remains the same, even though the area has changed. In the previous example, the “pushed-out” rectangle would be a \(12\text{ mm}\times23\text{ mm}\) rectangle, which means that \(P=2(12\text{ mm})+2(23\text{ mm})\), which simplifies to \(70\text{ mm}\). The approach of counting up every single side length, or the approach of “pushing-out” the rectangle’s corner will both result in the same answer.
More advanced perimeter problems might require you to “push-out” more than one corner of the figure. For example, in the figure below, we can determine the perimeter by finding the measure of all of the missing side lengths, or by “pushing-out” the corners to create a rectangle.
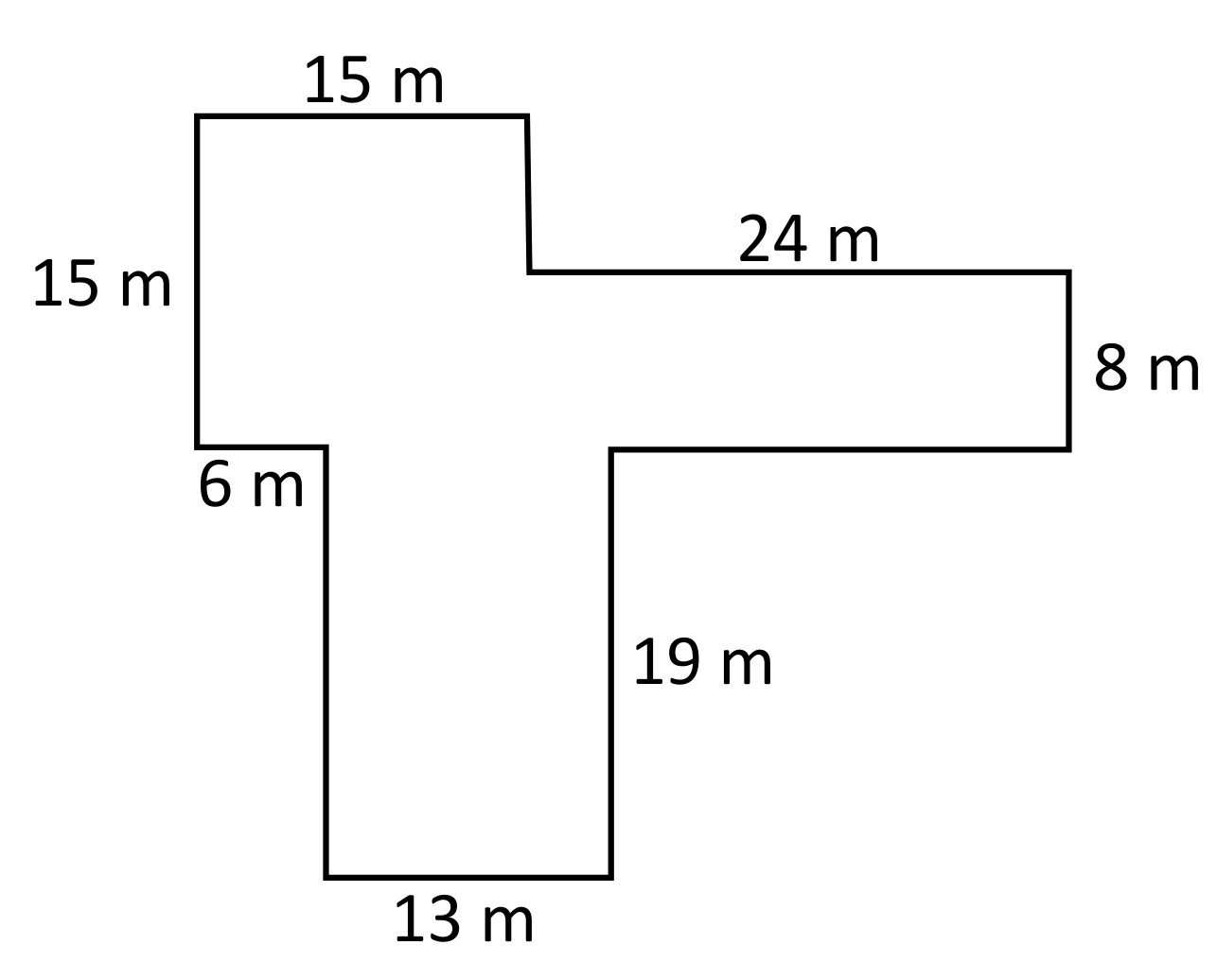
Missing side lengths approach
There are three missing side lengths in the irregular figure below. The green dimension is opposite the side labeled \(19\text{ m}\), so it is also \(19\text{ m}\). The total height of the figure is \(34\text{ m}(19\text{ m}+15\text{ m}=34\text{ m})\), therefore the blue dimension is \(34\text{ m}-8\text{ m}-19\text{ m}=7\text{ m}\). The total width of the figure is \(39\text{ m}(15\text{ m}+24\text{ m}=39\text{ m})\), so the pink dimension is found by subtracting \(39\text{ m}-6\text{ m}-13\text{ m}=20\text{ m}\). Now that all dimensions are solved for, the perimeter can be calculated by adding up each side length. This simplifies to \(146\text{ m}\).
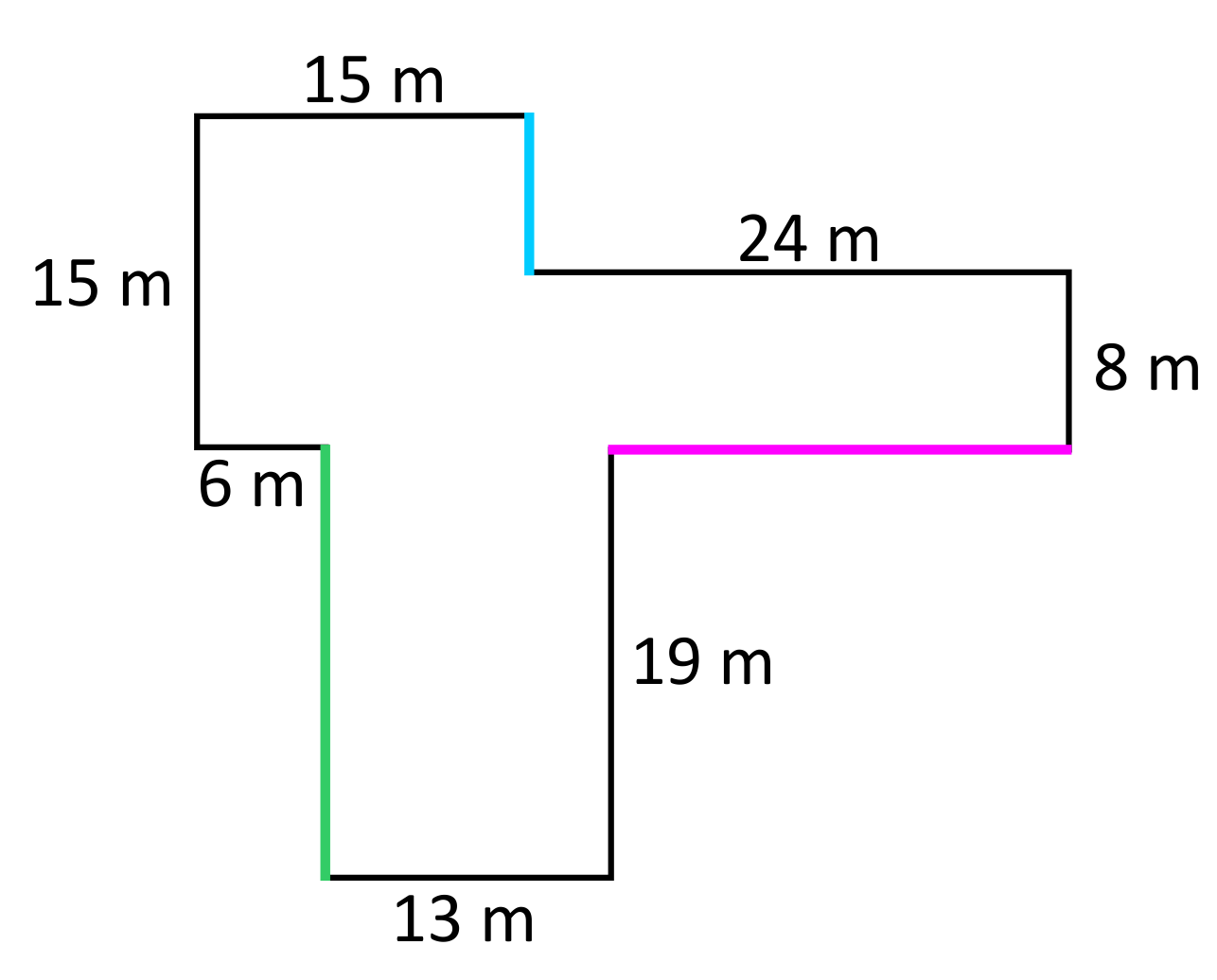
“Push-out” the corners approach
When the corners of the shape are “pushed-out”, the dimensions of the rectangle become \(34\text{ m}\times 39\text{ m}\). From here we can use the perimeter formula: \(P=2(34\text{ m})+2(39\text{ m})\), which simplifies to \(146\text{ m}\). As you can see, when the shapes are more complex, and more irregular, the “push-out” the corners approach saves time.
To re-cap, when you calculate the perimeter of a two-dimensional shape, you are finding the total distance around that shape. There are a variety of techniques used for finding the perimeter of a figure, such as perimeter formulas, “pushing-out” the corners of a rectangle, or simply adding up each individual side length. The strategy that you choose will often depend on what information is provided within the problem.
Perimeter Sample Questions
Here are a few sample questions going over perimeter.
Perimeter is defined as the _________ around a two-dimensional shape.
Perimeter is calculated by finding the distance around a two-dimensional shape. Perimeter can be determined by finding the sum of all side lengths of a figure. For example, the perimeter of a square, with side lengths of \(3\) inches, would be \(12\) inches \((P=3\text{ in}+3\text{ in}+3\text{ in}+3\text{ in})\).
Which item shows an incorrect perimeter formula?
\(\frac{1}{2}bh\) is the formula for a triangle’s area, not its perimeter. The perimeter of a triangle is found by adding the length of each side. \(P=s_1+s_2+s_3\) describes the sum of side \(1\), side \(2\), and side \(3\).
The border around a swimming pool needs to be tiled, but only four out of six side lengths of the pool have been measured. Use the provided dimensions to calculate the entire perimeter of the swimming pool.
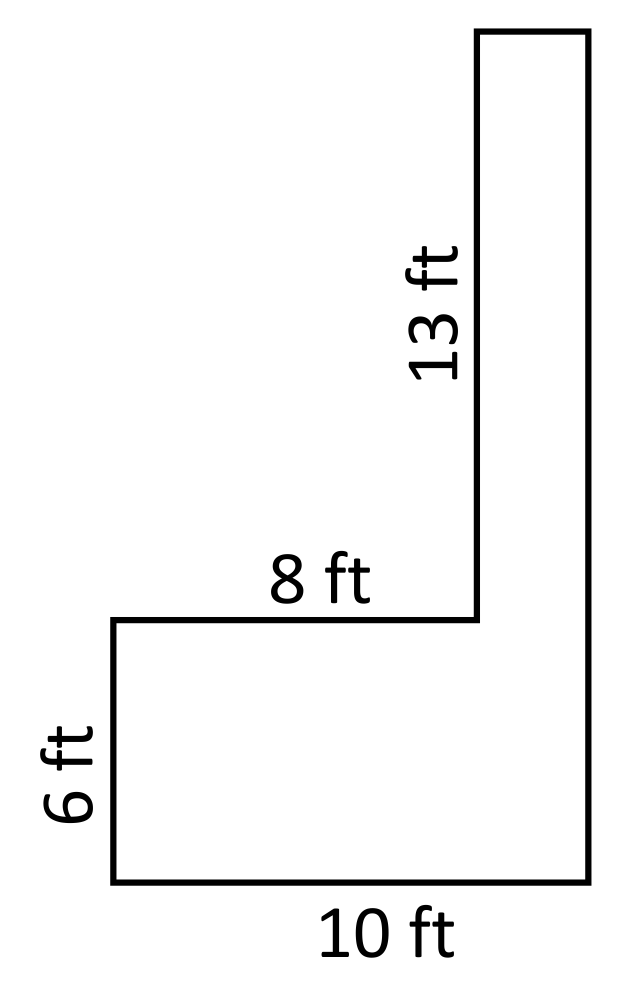
It can be helpful to visualize the shape of the swimming pool as a rectangle with one corner pushed in. Now imagine this corner being pushed back out, in order to create a full rectangular shape. The new rectangle now has a width
of 10 feet, and a length of 19 feet \((13\text{ ft}+6\text{ ft})\). The perimeter can now be calculated using the formula \(P=2l+2w\) which becomes \(P=2(19)+2(10)\) which simplifies to 58 feet.
Lacey is designing a large C-shape garden that will be bordered with a short fence. The fencing costs $14 per yard, and Lacy has a budget of $1,500 for the fencing project. Does she have enough money to cover the fencing cost?
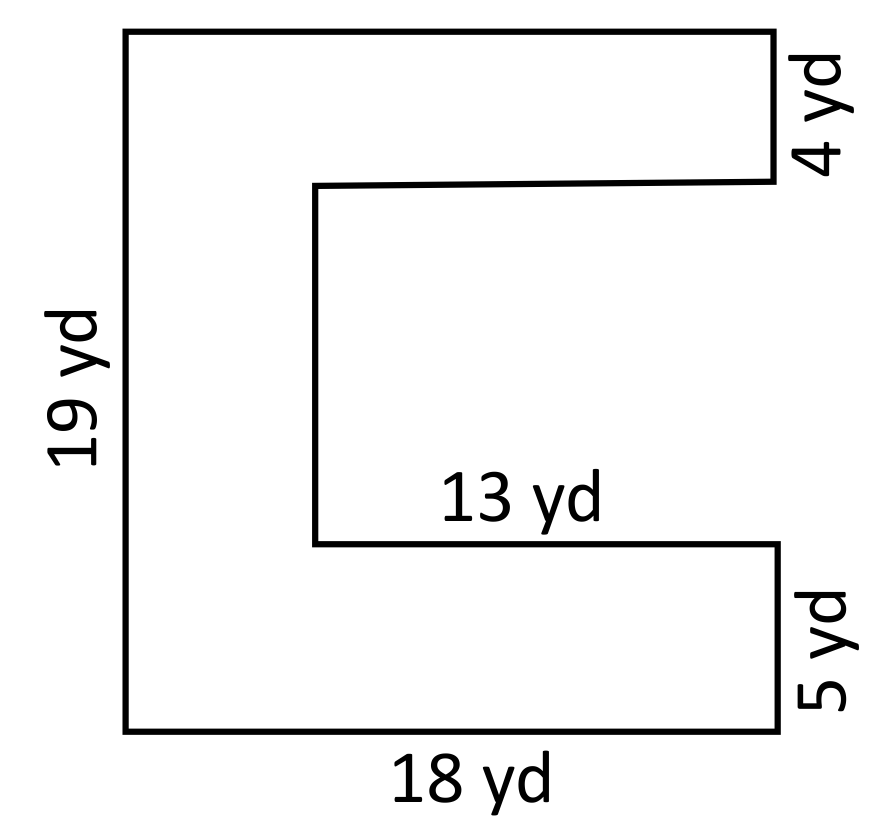
The fencing cost can be determined by calculating the perimeter of the garden. Five out of eight side lengths are provided, which is enough information to solve for the missing sides.
For example, the yellow side length is \(10\) yards because \(19\text{ yd}-5\text{ yd}-4\text{ yd}=10\text{ yd}\). The green side length is \(13\) yards because the opposite side length is \(13\) yards. The pink side length is \(18\) yards because the opposite side length is \(18\) yd. Now that all sides are accounted for, the perimeter can be calculated. The sum of all side lengths is \(100\) yards. The fencing costs \($14\) per yard, so the total fencing cost can be calculated as \(100\times$14=$1{,}400\). Lacey’s budget for the fencing project was \($1{,}500\) so she has enough money to complete the project.
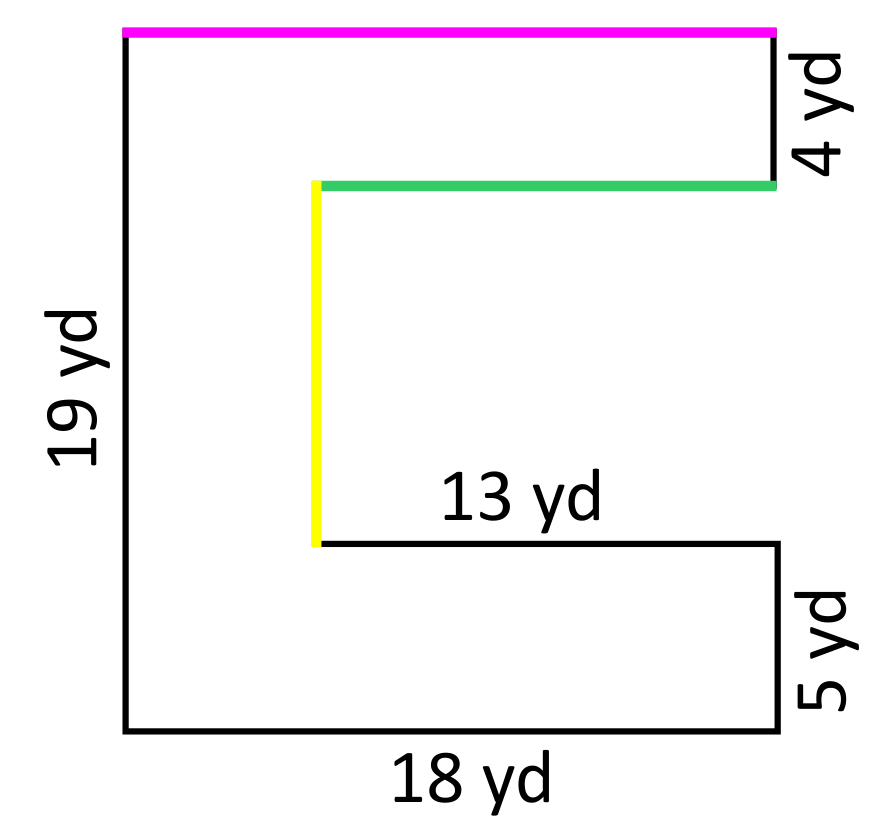
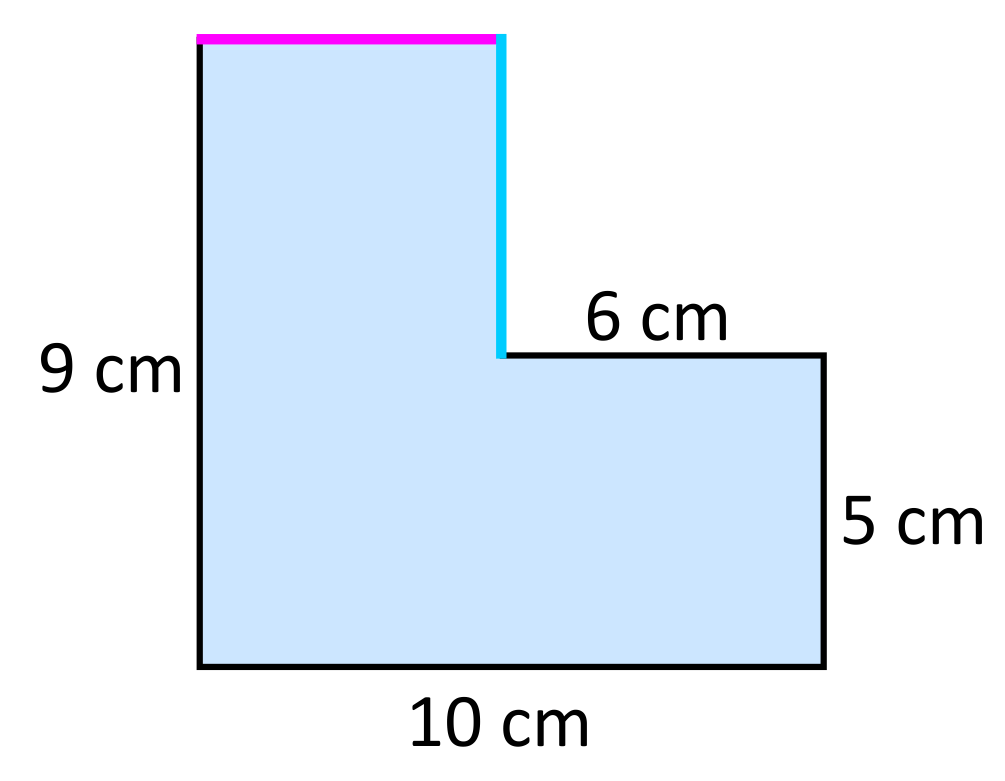
Student A claims that the two missing side lengths will be \(6\) cm and \(5\) cm because they appear to match the other two side lengths that are labeled \(6\) cm and \(5\) cm. Student B claims that the two missing side lengths will be \(4\) cm and \(4\) cm based on the other dimensions that are provided. Which student is correct?
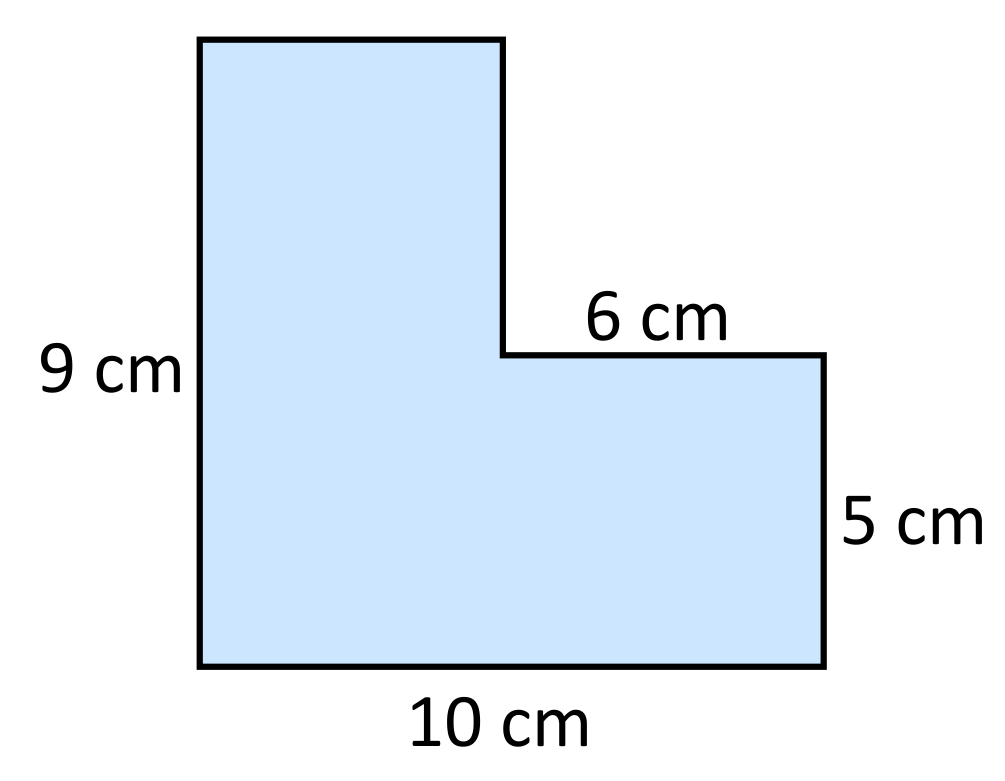
The pink side length can be identified by calculating \(10\text{ cm}-6\text{ cm}=4\text{ cm}\). The blue side length can be identified by calculating \(9\text{ cm}-5\text{ cm}=4\text{ cm}\). It is important to remember that even when side lengths “appear” to be obvious (Student A’s claim), it is important to prove their length using the other provided dimensions. In this case, student B is correct in stating that the two missing side lengths are both \(4\text{ cm}\).