
Hi, and welcome to this video on graphing linear equations!
In this video, we’re going to quickly review the various ways that linear equations can be written, and discover the best methods of graphing equations by hand based on the form that you are given.
Let’s get started!
The Importance of Graphing Linear Equations
When graphed, linear equations form a straight line on the \(x-y\) coordinate plane. The graph is a visual representation, and it is often useful to identify key features that are not immediately recognizable from the equation.
For example, when we look at a graph, we can see exactly where a line crosses the \(x\)-axis. This is useful because that \(x\)-value is the solution to the equation. Similarly, if we are given a system of equations, meaning one or more equations, we can find the solution of the system by graphing each line and finding the point of intersection, if it exists.
Knowing how to graph a linear equation by hand is an important skill. The graphing method that you will use will depend on the structure that is provided.
Review of Linear Equation Forms
Let’s quickly review the three forms:
An equation in standard form is written as \(Ax + By = C\), where \(A\), \(B\) and \(C\) are constants. \(A\) and \(B\) are known as coefficients of the variables \(x\) and \(y\), respectively.
An equation in slope-intercept form is written as \(y = mx + b\), where \(m\) represents the slope of the line, and \(b\) represents the \(y\)-intercept, which is the point on the \(y\)-axis where the line crosses.
An equation in point-slope form is written as \(( y – y_{1}) = m(x – x_{1})\). This form provides the ordered pair of a point, \((x_{1} , y_{1})\), that the line passes through and the slope of the line.
While the equations may look different, they all represent a line. When you are asked to graph an equation, you will want to choose the method that is most suitable based on what is provided. Let’s now take a look at each form and determine the graphing method that is the best for each.
Graphing from Standard Form
Let’s start with an example that uses standard form: \(Ax + By = C\).
A few algebraic steps are necessary in order to graph a line in this form. Keep in mind that you only need two points to graph a line, and using a straight edge to carefully draw the line through those points will provide more accurate results.
The two points that can be quickly calculated from this form are the \(x\)-intercept and the \(y\)-intercept. The graph here illustrates this process visually.
Let’s go through the steps to find the intercepts of the equation, \(2x + 3y = 12\):
The \(y\)-intercept can be determined by substituting \(x=0\) into the equation and solving for \(y\).
\(3y = 12\)
Divide by 3 on both sides because the 0 doesn’t matter; it won’t change anything.
\(y = 4\)
The line crosses the \(y\)-axis at the \(y\)-intercept, \((0,4)\).
Likewise, the \(x\)-intercept can be determined by substituting \(y=0\) into the equation and solving for \(x\), as follows:
\(2x = 12\)
Divide by 2 on both sides, because again, the 0 won’t change anything.
\(x = 6 \)
So the \(x\)-intercept is at the point \((6,0)\).
Once the intercepts are plotted at the points \((0,4)\) and \((6,0)\), you are ready to graph the line. The line passes through these points, and arrows at the ends should be drawn to indicate that the line extends forever in both directions.
This is an easy method of graphing an equation in standard form if the constant, C, is a multiple of the coefficients, A and B. Accordingly, this method of graphing is called the “intercept method.”
Let’s try another example problem:
Graph the equation \(3x – 4y = 12\).
This equation is in standard form and the constant, 12, is a multiple of both 3 and 4. Therefore, using the intercept method to graph is a good method.
As before, determine both the \(y\)– and \(x\)-intercepts:
To find the \(y\)-intercept, let \(x=0\) in the standard form equation and solve for \(y\), as shown:
\(-4y = 12\)
\(\frac{-4y}{-4}=\frac{12}{-4}\)
\(y = -3\)
So our \(y\)-intercept is at the point \((0,-3)\).
The \(x\)-intercept can be determined by substituting \(y=0\) into the equation and solving for \(x\):
\(3x = 12\)
\(\frac{3x}{3}=\frac{12}{3}\)
\(x = 4\)
This means our \(x\)-intercept, or the point where our graph crosses the \(x\)-axis, is \((4,0)\).
So our 2 points we’re gonna use to graph are \((0,-3)\) and \((4,0)\).
Graph this line by plotting the intercepts and drawing a straight line extending through the points, like so: (see image at 6:00)
Graphing from Slope-Intercept Form
Okay, now let’s try slope-intercept form: \(y = mx + b\).
If you are given a standard form equation but the constant, \(C\), is not a multiple of the coefficients A and B, then converting the equation into slope-intercept form will provide the information needed for a more accurate graph.
To convert to slope-intercept form, simply solve the standard form equation for \(y\).
Consider the standard form equation, \(3x + 2y = 4\). You notice immediately that while 4 is a multiple of 2, it is not a multiple of 3. A better way to graph this line is to first convert it to slope-intercept form by solving for the variable \(y\).
To do this, we take our equation \(3x+2y=4\) and subtract \(3x\) from both sides.
This gives us \(2y=4-3x\).
Now we want to divide by 2. When we divide the whole equation by 2, it’s also the same as dividing each part by 2.
So we’re going to do \(y=2-\frac{3}{2}x\).
Now, this equation looks similar to what we want but it’s not quite right. We want our \(x\) to be in front.
Since we’re adding, we can flip this without worrying about changing anything.
The resulting equation, \(y=\frac{-3}{2x}+2\), is in slope-intercept form, where the slope of this line is shown, \(m = \frac{-3}{2}\). The constant in this equation, \(b=2\), represents the point where the line crosses the \(y\)-axis, the point \((0,2)\).
To graph a line in this form, plot the \(y\)-intercept at \((0,2)\). A second point on the line is plotted by moving in a vertical direction, often referred to as the “rise,” and then a horizontal direction, referred to as the “run.” These directions are known by looking at the slope, \(m=-{3}{2}\).
Because the numerator of the slope is -3, move 3 units down from the \(y\)-intercept. From there, move 2 units to the right, as indicated by the denominator of the slope, 2.
Note: A positive “rise” will be up, and a negative “rise” is down; a positive “run” is right, a negative “run” is left.
This movement from the \(y\)-intercept brings you to another point that is on the line, \((2,-1)\). With two points plotted, you can graph the straight line that extends through them.
Now let’s try this out with another example problem:
Graph the equation \(y=\frac{2}{3}x-1\). This equation is already in slope-intercept form.
The slope is identified as \(m=\frac{2}{3}\), and the \(y\)-intercept is at the ordered pair, \((0,-1)\). That is where the graphing begins. Plot the first point at the \(y\)-intercept, then move from that point according to the slope. Both numerator and denominator are positive, so the “rise” is up 2 and the “run” is right 3.
This brings you to the second point that is needed to graph the line, \((3,1)\). Carefully draw a line that extends through these two points.
Graphing from Point-Slope Form
Okay, now to our third and final form, point-slope form: \(( y – y_{1}) = m(x – x_{1})\).
As noted, the point-slope form of an equation names a point, \((x_{1} , y_{1})\), that the line travels through. It also provides the slope. So, graphing a line in this form is similar to the process we detailed before. The exception is that rather than starting at the \(y\)-intercept, the first point of the graph is at the point \((x_{1} , y_{1})\). Identifying that point sometimes causes some confusion.
Note that the point-slope form subtracts the y-coordinate of the point, \(y_{1}\), from the variable \(y\), and the \(x\)-coordinate of the point \(x1\) is subtracted from the variable \(x\). Notice how the point is identified with the following examples:
In this first example, the line passes through the point \((2,3)\). The line in the second example runs through points \((1,2)\). In the third example, the line passes through the points \((7,-5)\).
Example 3 requires some explanation because the \(y\)-coordinate of the point is added to the \(y\)-variable in the equation, rather than being subtracted. As a result, an adjustment must be made to the equation to identify the point.
Remember, when you subtract a negative value, it has the same effect as addition. As a result, rewriting the equation to reflect subtraction is allowable.
The adjusted equation looks like this: \( y- (-5) = 3(x – 7)\). Now the point, \((x_{1} , y_{1})\), is recognizable as \((7,-5)\).
Here is another example of a point-slope equation that deserves some attention: \(y=12(x-4)\).
This equation is unique because there is no y-coordinate being subtracted from the \(y\)-variable. To identify the point, rewrite the equation as: \(y-0=12(x-4)\). Now the point can be seen as the \(x\)-intercept, \((4,0)\).
Now that the first point can be identified from point-slope form, use the slope to move from that point to another point on the line using slope.
Okay, let’s go over two more examples.
Graph the following equation: \(y – 3 = 4(x – 2)\).
Identify and plot the first point, \((2,3)\). Slope is \(m=4\). This value can be represented by the equivalent fraction, \(\frac{4}{1}\).This slope translates to a “rise” of up, 4 and a “run” of right, 1.
This brings you to another point on the graph, \((3,7)\). The line can then be graphed extending through these two points.
Graph the following equation: \(y-2= -\frac{1}{3}(x-1)\).
Identify and plot the first point, (1, 2). Slope in this equation is a negative. At this stage, you can decide to move the rise or the run in the negative direction. For this example, let’s consider the rise, or the numerator, to be the negative value: \(m=\frac{rise}{run}=\frac{-1}{3}\).
This translates to a “rise” of down, 1; and a “run” of right, 3. The position of the second point on the line is at \((4,1)\).
The line is graphed by drawing a line extending through these two points.
Now that you have had some practice identifying the features of linear equations in various forms, you can recognize why there are different graphing methods. A quick analysis of the equation should give you direction on how to proceed with the graphing process.
I hope this review was helpful! Thanks for watching, and happy studying!
Graphing Linear Equations Practice Questions
Convert the linear equation from standard form to slope-intercept form:
\(5x+4y=8\)
To convert to slope-intercept form, solve the standard form equation for y.
\(5x+4y=8\)
First, move 5x to the right side of the equation by using inverse operations. Since the opposite of addition is subtraction, subtract 5x from both sides of the equation.
\(5x+4y-5x=8-5x\)
\(5x-5x=0\), so we are left with \(4y\) on the left side of the equation.
\(4y=8-5x\)
To isolate the variable \(y\), use inverse operations. Since the opposite of multiplication is division, divide both sides of the equation by 4.
\(\frac{4y}{4}=\frac{8-5x}{4}\)
\(4÷4=1\), so we have 1y (which can also be written as y). \(8÷4=2\) and \(5x÷4=54x\).
\(y=2-\frac{5}{4}x\)
Last, switch the order of the two terms so the x-term comes first. Since \(\frac{5}{4}x\) is subtracted, it becomes a negative term when switched. Since 2 is a positive number, it is added to \(-\frac{5}{4}x\). Therefore, the correct answer is D.
\(y=-\frac{5}{4}x+2\)
Consider the following linear equation written in standard form: \(6x-4y=24\)
What are the coordinates for the x-intercept and the y-intercept?
Solve for y when x=0 to identify the x-intercept, and solve for x when \(y=0\) to identify the y-intercept. See work shown below:
Starting with the equation in standard form, solve for x when \(y=0\) to identify the x-intercept.
\(6x-4y=24\)
Substitute y with 0 to solve for x.
\(6x-4(0)=24\)
Since \(4\times0=0\), replace \(4y\) with 0 in the equation.
\(6x-0=24\)
Next, isolate the variable x by using its inverse operation. Since the opposite of multiplication is division, divide both sides of the equation by 6.
\(6x\div6=24\div6\)
\(6÷6=1\), so we have \(1x\) (which can also be written as x). \(24÷6=4\), so \(x=4\). Therefore, the x-intercept is 4, or \((4,0)\).
\(x=4\)
Going back to the original equation in standard form, solve for y when \(x=0\) to identify the y-intercept.
\(6x-4y=24\)
Substitute x with 0 to solve for y.
\(6(0)-4y=24\)
Since \(6\times0=0\), replace \(6x\) with 0 in the equation.
\(0-4y=24\)
Next, isolate the variable y by using its inverse operation. Since the opposite of multiplication is division, divide both sides of the equation by -4.
\(-4y\div-4=24\div-4\)
\(-4÷-4=1\), so we have \(1y\) (which can also be written as y). \(24÷-4=-6\), so \(y=-6\). The y-intercept is -6, or \((0,-6)\).
Carly pays 5 dollars to rent a bicycle to go for a ride along the river trail. For each hour she rents the bike, Carly pays an extra 2 dollars. This scenario is illustrated in the graph below. Which equation represents the scenario and corresponding graph?
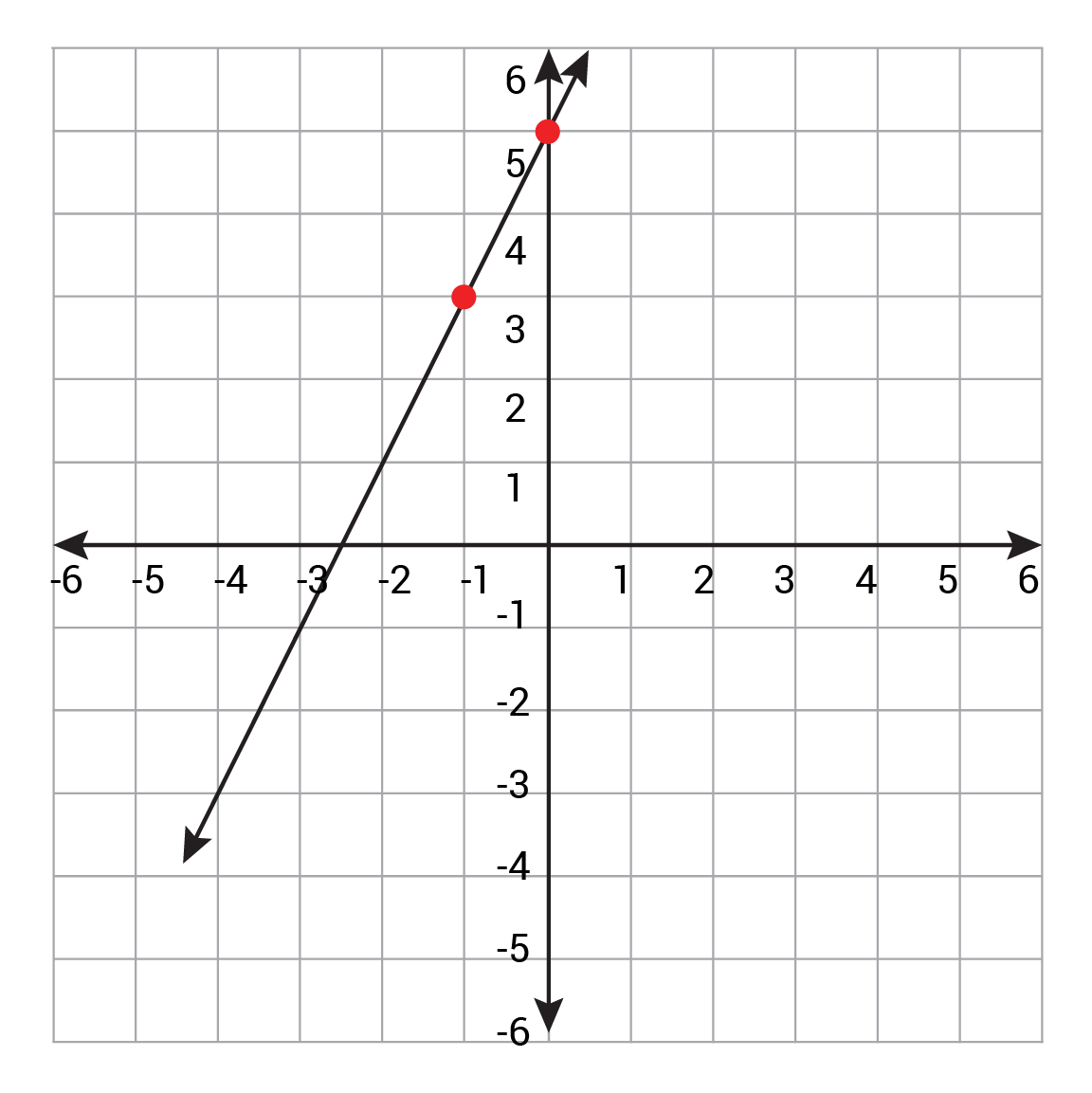
Since the graph of the line intercepts the y-axis at \((0,5)\), the value for b in slope-intercept form \(y=mx+b\) must equal 5. To determine the slope (m), calculate the rise over run of the two points shown on the graph \((0,5)\) and \((-1,3)\). Calculate the change in y-coordinates and divide by the change in x-coordinates. \(5-3=2\) and \(0-(-1)=1\). \(2÷1=2\), so the slope (m) is 2. Therefore, the correct answer is B.
Given the following linear equation in point-slope form, what point does it pass through when graphed?
\(y-8=\frac{1}{4}(x+3)\)
When a linear equation is written in point-slope form, the y-coordinate of the point, \(y_1\), is subtracted from the variable y. Likewise, the x-coordinate of the point, \(x_1\), is subtracted from the variable x.
\(y-y_1=m(x-x_1)\)
\(y-8=\frac{1}{4}(x+3)\)
Notice that in this equation, the x-coordinate is added to x instead of subtracted. Remember that subtracting a negative number has the same result as adding. We can rewrite the formula as follows:
\(y-8=14(x-(-3))\)
The x-coordinate is -3, and the y-coordinate is 8. Therefore, D is the correct answer.
Karen pays 224 dollars in advance for her gym membership, which is kept in an account. Each time she visits the gym, 7 dollars is deducted from her account. Which equation represents the value of Karen’s account after x visits to the gym?
Karen starts with $224 in her account. This is shown as a positive number in the equation. Each time Karen visits the gym, $7 is deducted. This is shown as a negative number in the equation. -7 is multiplied by x because $7 is deducted for each visit to the gym, represented by x. C is correct because this equation contains the terms -7x and +224.
