
Hi, and welcome to this video on roots! Today, we will be working towards an understanding of the terminology, notation, and interpretation of algebraic roots. We will also be making connections to other concepts that you will need in higher-level math. Let’s get started!
Understanding Terminology
Understanding the terminology and notation of math is half the battle if you’re struggling to grasp certain concepts. This is true of roots, where the terminology that is used determines the “type” of root that is evaluated.
Finding the Square Root
To find the square root of a number, simply ask yourself, “what value, when multiplied by itself, results in that number?”
For example, let’s say you were asked to find the square root of 4. Ask yourself, “what value, when multiplied by itself, results in 4?” The answer is 2, because 2 times 2 equals 4.
Let’s try another one. What is the square root of 121? Ask yourself, “what value, when multiplied by itself, results in 121?” The answer is 11, because 11 times 11 equals 121.
Finding the Cube Root
To find the cube root of a number, ask yourself, “what value, when multiplied by itself three times, results in that number?”
For example, the cube root of 8 would be 2, because 2 times itself three times equals 8. The cube root of 64 is 4, because 4 times itself three times equals 8. Four times four is 16, 16 times 4 is 64.
\(4 \cdot 4=16\)
\(16 \cdot4=64\)
Fourth roots, fifth roots, sixth roots, and so on, can be found similarly.
Perfect Squares
There is an important relationship revealed in these practice problems. We just showed that 2 is the square root of 4. That means that the number 4 is a perfect square. Knowing the perfect squares from 1 through 144 is helpful in order to simplify radicals in the future. The table here shows these perfect squares as related to their square roots.
| Perfect Squares | ||
|---|---|---|
| \(1^2=1\) | \(5^2=25\) | \(9^2=81\) |
| \(2^2=4\) | \(6^2=36\) | \(10^2=100\) |
| \(3^2=9\) | \(7^2=49\) | \(11^2=121\) |
| \(4^2=16\) | \(8^2=64\) | \(12^2=144\) |
Perfect Cubes
Perfect cubes can also be quickly determined by multiplying any integer by itself three times. In one of the previous examples, we showed that 4 is the cube root of 64. This means that 64 is a perfect cube.
| Perfect Cubes | |
|---|---|
| \(1^3=1\) | \(6^3=216\) |
| \(2^3=8\) | \(7^3=343\) |
| \(3^3=27\) | \(8^3=512\) |
| \(4^3=64\) | \(9^3=729\) |
| \(5^3=125\) | \(10^3=1,000\) |
As revealed in the table above, perfect cubes increase rapidly!
Notation
Radical
To generalize the rule of finding roots, let’s introduce the notation of radicals. Let’s break down this notation into “parts” by looking at the cube root of 27, which looks like this: \(\sqrt[3]{27}\).
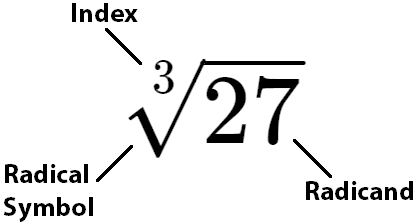
The radical may resemble a division symbol, but it has a very different meaning.
Radicand
What is under the radical symbol is called the radicand, and this can be a number or an algebraic expression. We are going to stick to numbers in this video.
Index
The index is the most important feature. That small number placed in the “checkmark” of the radical symbol indicates the root. In this example, because the index is 3 they are asking for the cube root of 27. With a bit of thought, we can determine that 3 times 3 times 3 equals 27, so the cube root of 27 is 3, which means that 27 is a perfect cube.
It is important to note that the square root symbol does not show an index of 2. So just remember that when there is NO index indicated, the radical represents a square root by default.
Exponent Notation
For our final point in this video, let’s make an important link from radical notation to exponen notation.
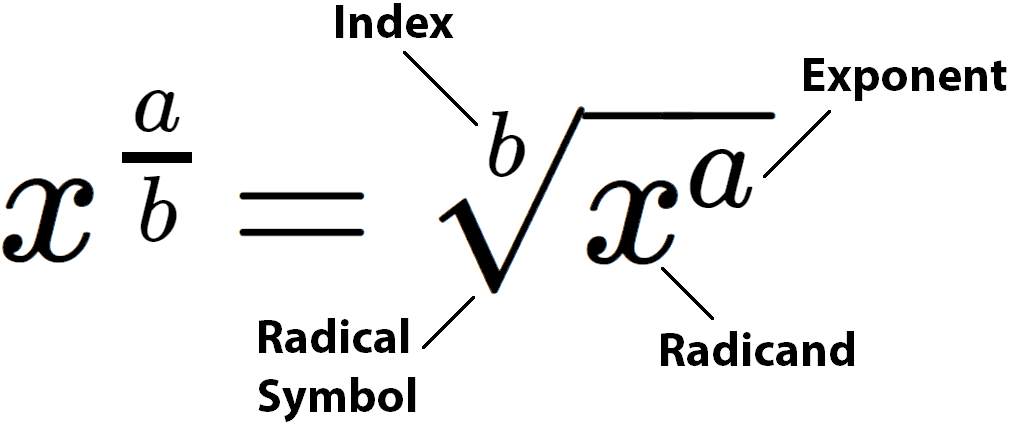
A radical is the same as raising a base to a fractional exponent, where the index of the radical becomes the denominator of the fractional exponent and the exponent of the radicand is the numerator of the fractional exponent. Here is a generalized example:
Let’s say that the radicand of a radical is \(x^a\), and the index of the radical is \(b\). This is equivalent to raising a base, \(x\), to the fractional exponent of \(\frac{a}{b}\).
Practice Problems
Practicing a few examples will help to make some sense of all of this notation and terminology.
Problem #1
First, let’s practice expressing a radical as a fractional exponent: \(\sqrt[3]{x^2}\)
Remember, the index of the radical becomes the denominator of the fractional exponent, which in this case is 3. The exponent of the radicand becomes the numerator of the fractional exponent, which is 2 in this case. So, our fractional exponent is \(x^{\frac{2}{3}}\):
Problem #2
Let’s try another one: \(\sqrt[4]{3}\)
So we know that our index, 4, becomes the denominator, but the radicand doesn’t have an exponent. That means that 1 will become our numerator, which gives us \(3^{\frac{1}{4}}\):
Now let’s flip things around and convert a fractional exponent to a radical. Our fractional exponent is \(125^{\frac{1}{3}}\).
If we reverse what we were doing before, the denominator of the fractional exponent becomes the index of our radical. Since the numerator here is 1, we don’t have an exponent for the radicand, so we end up with \(\sqrt[3]{125}\):
Once the conversion to a radical is made, the problem becomes more familiar and the root is easier to evaluate: The cube root of 125 is 5.
I hope this review was helpful! Thanks for watching, and happy studying!
Frequently Asked Questions
Q
What is a root in math?
A
The root of a number in math is a number that when multiplied by itself produces the original number. For example, the square root of \(49\) is \(7\) because \(7\times7=49\). In this case, because \(7\) is multiplied by itself twice to produce \(49\), we call \(7\) the square root of \(49\). The cube root of \(27\) is \(3\), because \(3\times3\times3=27\). Since \(3\) is multiplied three times to produce \(27\) we call this a cube root, so \(3\) is the cube root of \(27\).
Q
How do you find the roots in math?
A
To find the root of a number in math, we start by finding the factors of that number. For example, the factors of \(64\) are \(2\times2\times2\times2\times2\times2\). If we look a bit closer, we see the factors can also be written as \(8\times8\):
So we know that the square root of \(64\) is \(8\) because \(8\times8=64\). Since \(8\) is being multiplied by itself twice we call this the square root of \(64\).
We can also bunch the factors into three groups: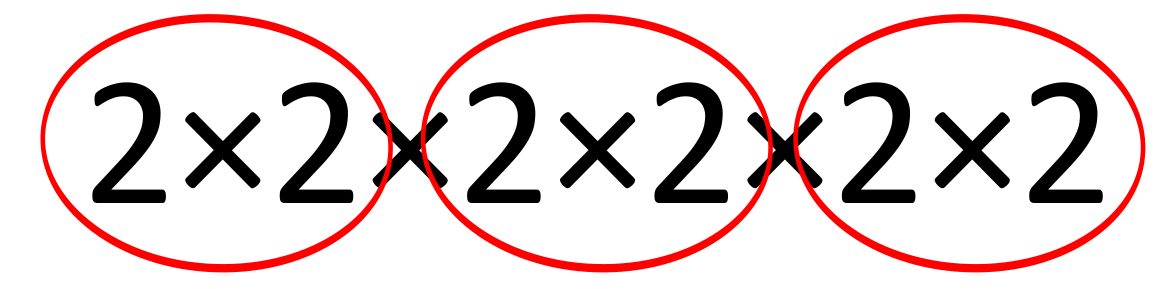 This means \(4\times4\times4\) also equals \(64\). Since \(4\) is multiplied by itself three times to get \(64\), we know that \(4\) is the cube root of \(64\).
This means \(4\times4\times4\) also equals \(64\). Since \(4\) is multiplied by itself three times to get \(64\), we know that \(4\) is the cube root of \(64\).
Q
What does a \(\sqrt{ }\) mean in math?
A
This is the symbol that represents square root. The square root of a number is the number when multiplied by itself produces the original number. For example, the square root of \(16\), or \(\sqrt{16}\), is \(4\), because \(4\times4=16\).
Q
What is the easiest way to find cube roots?
A
The cube root of a number is a number that is multiplied by itself \(3\) times to give the original number. The easiest way to find the cube root of a number is to start by finding the factors and see if there are \(3\) numbers in the factor that are the same. For example, to find the cube root of \(125\), we will start by finding the factors, which are \(5\times5\times5\). Since \(5\) is being multiplied by itself three times to produce \(125\), we can say that \(5\) is the cube root of \(125\).
Q
What is a radical in math?
A
A radical in math is the symbol \(\sqrt{ }\), which is used to represent a root. If there is no index (number in the “arm” of the radical), then it is assumed to be a square root. To represent the expression “square root of \(36\)”, we place the \(36\) under the radical like so: \(\sqrt{36}\). A square root is a number that when multiplied by itself will produce the original number under the radical. Therefore, the square root of \(36\) is equal to \(6\) because \(6\times6=36\). This can also be written as \(\sqrt{36}=6\).
Q
How do you solve a radical?
A
To solve a radical, which represents a square root, we start by finding the factors of the number that is under the radical. For example, to solve \(\sqrt{49}\), we find the factors of \(49\), which are \(7\times7\). Since \(7\) is being multiplied by itself twice, we can conclude that \(7\) is the square root of \(49\). Therefore, \(\sqrt{49}=7\).
Q
What is a radical simplified?
A
To simplify a radical, you must find the square root of the number until nothing under the radical has any roots. For example, we can simplify the radical \(\sqrt{18}\) by finding the factors of \(18\), which are \(3\times3\times2\). Since \(3\) is multiplied twice by itself, we can pull that root out and the \(3\) would go in front of the radical, while the \(2\) remains under the radical. \(\sqrt{18}=3\sqrt{2}\), which is the most simplified form of the expression because you cannot simplify \(\sqrt{2}\).
Q
What is an example of a radical number?
A
A radical is a symbol that represents square root. The number under the radical is called a radicand. For example, the expression “the square root of 81”, is represented in math by the radical symbol with \(81\) under the radical. The \(\sqrt{81}=9\) because \(9\times9=81\). The symbol is the radical, the \(81\) is the radicand, and the \(9\) is the root.
Q
What is a radicand of a square root?
A
The radicand is the number under the radical that we are trying to find the root for. For example, the “square root of \(100\)” can be written as \(\sqrt{100}\). The number under the symbol, which is called the radical, is called the radicand. In this case, \(100\) is the radicand.
Q
What is the index and radicand?
A
The index is the root that we are trying to find, and the radicand is the number under the radical symbol.
For example, \(\sqrt{25}\) is the square root of \(25\). There is an imaginary \(2\) that we do not write, which tells us that we should be taking the square root of the number. In this case, \(2\) is the index and \(25\) is the radicand. The expression, \(\sqrt[3]{64}\), is the cube root of \(64\). The \(3\) is the index, the \(64\) is the radicand, and the square root symbol is called the radical.
The index tells us which root of the radicand we are supposed to find. In the square root of \(25\) case, we are finding a number that is multiplied by itself twice to get \(25\). In the cube root of \(64\), we are looking for a number that is multiplied by itself three times to get \(64\).
Q
What is the difference between a radical and a radicand?
A
The radical is the symbol that represents square root. The radicand is the number that is under the radical that we are trying to find the root of. For example, in the expression \(\sqrt{50}\), the symbol is the radical and \(50\), which is under the radical symbol, is called the radicand.
Q
What is an example of a radicand?
A
A radicand is the number under the radical. In the expression, the square root of \(36\), which can also be written using math symbols as \(\sqrt{36}\), the \(36\) is the radicand because it is under the radical, which is the square root symbol.
Root Practice Questions
What is \(\sqrt[3]{x^4}\) expressed as a fractional exponent?
The correct answer is \(x^\frac{4}{3}\). When turning a root into a fractional exponent, the number in the hook of the radical symbol, 3 in this case, becomes the denominator of the fractional exponent. The power, 4, of the base, x, becomes the numerator. The base stays the same, so \(\sqrt[3]{x^4}=x^\frac{4}{3}\).
What is \(x^\frac{7}{2}\) expressed as a radical?
The correct answer is \(\sqrt{x^7}\). When turning a fractional exponent into a radical, the numerator of the fraction becomes the exponent the base is raised to inside a radical symbol with the denominator of the fraction as the index. So \(x^\frac{7}{2}=\sqrt[2]{x^7}\), which can also be written as \(\sqrt{x^7}\) because no index is always assumed to be 2.
\(\sqrt{256}=\)
The correct answer is 16. To find the square root of 256, ask what number times itself gives you 256. \(16×16=256\), so \(\sqrt{256}=16\).
\(\sqrt[3]{64}=\)
The correct answer is 4. To find the cube root of 64, ask what number times itself three times gives you 64. \(4×4×4=64\), so \(\sqrt[3]{64}=4\).
What is the name of the small number placed in the “checkmark” of the radical symbol?
The correct answer is index. The index is the small number place in the “checkmark” of the radical symbol and indicates the root.
