
Hello, and welcome to this video on domain and range! In this video, we will see:
- What domain and range are
- And how to find the domain and range of a function
Remember, a function is a relation between two sets of numbers, an input and an output. Each element of the input produces a unique element of the output.
What is Domain?
The domain of a function is the set of all possible inputs of a function. This means it is any number you can plug into a function. For most functions, this will be any number you can plug in for the letter \(x\). Almost every time, your domain will be all real numbers, except for a few special cases like square root functions and rational numbers.
What is Range?
The range of a function is the set of all of the possible outputs of a function. Typically, this will be represented by the letter \(y\) or \(f(x)\). The range is any number that you can get when you plug in any number for \(x\).
Linear Functions
Let’s look at a simple linear function: \(y = 4x + 3\). We are going to find the domain and range using just the equation, by looking at a graph, and by looking at a table.
Let’s think about this algebraically for a minute. The domain is any number we can put in place of the \(x\). You could put 1, 2, -7, 84, or any other number in place of the \(x\). This means that the domain is: \(-\infty\leq x\leq\infty\). Another way to say this is that the domain is the set of all real numbers.
What about our range? Well, if I plug in 1 for \(x\), I get 7 and if I plug in 2 for \(x\), I get 11. But I can also plug in 1.5 for \(x\), which would give me 9, or 1.25 for \(x\), which would give me 8. I can plug in any decimal number, so for this equation, I can also get out any number for \(y\) by searching for the right \(x\).

The range of this function is also the set of all real numbers.
Now I want to check this graphically. If we graph this function, we see that it is a line. Lines continue across every value of \(x\) and every value of \(y\). This matches up with what we found out by thinking through it algebraically. This further proves that domain and range are both the set of all real numbers.
Now let’s look at a table of values for the first four terms of this function.
| \(x\) | \(y\) |
|---|---|
| 1 | 7 |
| 2 | 11 |
| 3 | 15 |
| 4 | 19 |
In this case, we are only looking at a portion of the function, so our domain of values would be {1, 2, 3, and 4} and our range of values would be {7, 11, 15, and 19}.
Let’s try a couple of examples. What is the domain and range of the function \(y=x^{2}-4x+3\)?
The domain is the list of numbers that can be plugged in for \(x\). You can plug in any number for \(x\), so the domain is the set of all real numbers.
What about our range? Let’s figure this out by looking at a graph of the equation.
Remember, our range is every possible value for \(y\). If we look at our graph, we see that it is a parabola that opens up with a vertex at \((2, -7)\).
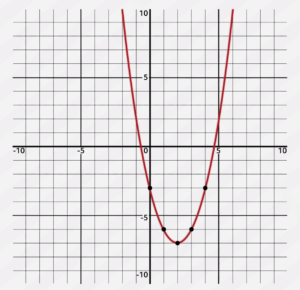
This means that our range is \(y\geq-7\).
Let’s try one more example, this time using a table for the function \(y=2x–1\).
| \(x\) | \(y\) |
|---|---|
| 7 | 13 |
| 14 | 27 |
| 21 | 41 |
| 28 | 55 |
What would be our domain and range given this table? Our domain would be {7, 14, 21, and 28} and our range would be {13, 27, 41, and 55}.
If we wanted the domain and range for the whole function, we would consider what numbers we can plug in for \(x\) and what corresponding \(y\)-values we would get. Well, we can plug in any number for \(x\), and it is a linear function, so we can get any number for \(y\). Therefore, the domain and range of this function is all real numbers.
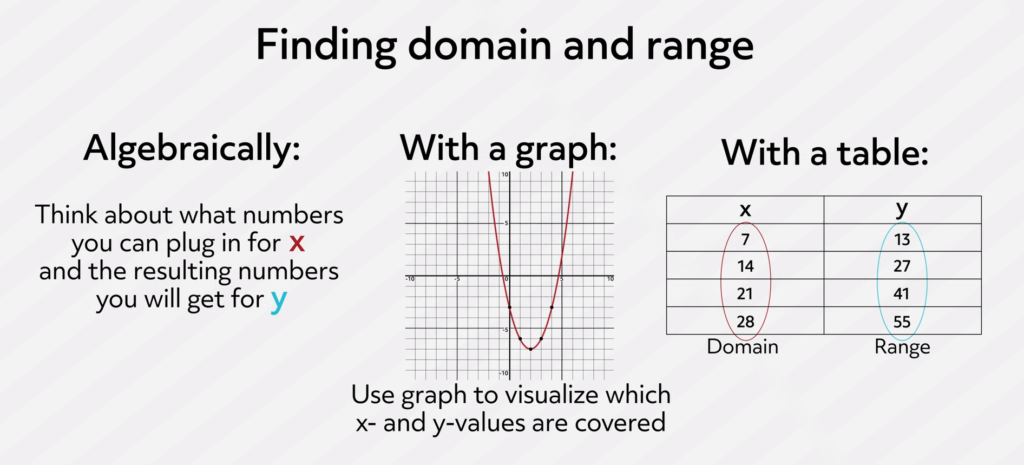
Remember, if you are finding the domain and range of a function algebraically, think about what numbers you can plug in for \(x\) and the resulting numbers you will get for \(y\). If you are finding the domain and range given a graph, follow your finger along the graph and see what \(x\)-values it covers and what \(y\)-values it covers.
Finally, if you are looking at a table, the domain is the list of numbers inputted for \(x\) and the range is the list of numbers that are the outputs of those \(x\) inputs, the numbers in the \(y\) column.
I hope this video on domain and range was helpful! Thanks for watching and happy studying!
Domain and Range Practice Questions
The linear equation \(y=2x+3\) is graphed below. Use the graph to determine the domain and range. Remember that the red line continues off the page indefinitely in both directions.
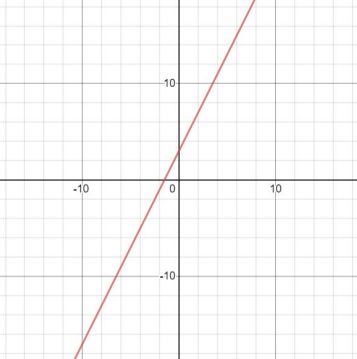
The correct answer is Domain: all real numbers | Range: all real numbers. The domain refers to all possible inputs that you can plug into the function. In this case, the red line on the graph shows that any value can be plugged in for x, therefore the domain is all real numbers. To find the range, look for all possible outputs of the function, or all values for y that appear on the graph. The graphed red line reveals that any value for y is possible, which means the domain is also all real numbers.
The quadratic function \(y=x^2+4x+3\) is graphed below. Use the graph to determine the domain and range.
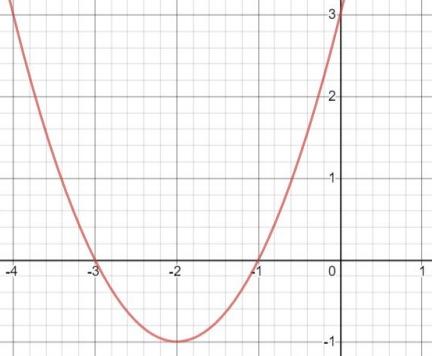
The correct answer is Domain: all real numbers | Range: y ≥ -1. The graph shows that all values of x are represented somewhere on the red line, because the line reaches out to the left and right and doesn’t end. This means the domain is all real numbers. However, when looking at the range, notice that the red line stops at -1 for y values. This means that values for y are only at or above -1, which is represented by y ≥ -1.
The table below represents only the first four terms of a function. This is only a small portion of the data that could be represented from the graph of \(y=-2x+7\). Which values represent range?
| A | B |
| 1 | 5 |
| 2 | 3 |
| 3 | 1 |
| 4 | -1 |
The correct answer is Column B. This can be determined by plugging in a value on the left into the equation. The result is the value on the right. Every value on the left is an input, and every value on the right is an output. For example, if we plug in 1 for x, we get 5 as the output for y.
Find the domain and range for the linear equation \(y=5x+7\).
The correct answer is Domain: all real numbers | Range: all real numbers. The domain and range for this linear equation can be determined algebraically. There is nothing that prevents plugging in any value for x, so the domain is all real numbers. The y values, or outputs, are simply a reflection of what is input. Since any value can be plugged in for and this is a linear equation, the values for y are also unlimited. The values for x are unlimited as well as the values for y, so the range is also all real numbers.
Which table shows the correct domain and range for the linear equation \(y=2x+3\)?
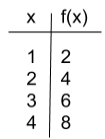
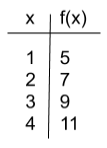
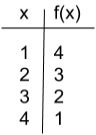
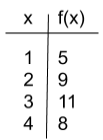
The correct answer is B. Input values are represented by x, and f(x) represents the output values, or y. Table B can be tested algebraically to make sure that each input value results in the appropriate output value. If 1 is plugged in for x, the result is 5. If 2 is plugged in for x, the result is 7. Table B shows input and output values that match with the given equation.
