Set Operations with Venn Diagrams

When it comes to set theory and set operation problems, it can often be helpful to visualize the problem with a picture. Venn diagrams are helpful tools for doing exactly that.

A Venn diagram is typically drawn with two overlapping circles. Each circle represents a set, and the middle area where they overlap represents items that belong to both sets. For example, we can make a Venn diagram which shows how the set of round fruits and the set of red fruits are distinct but have some overlap:

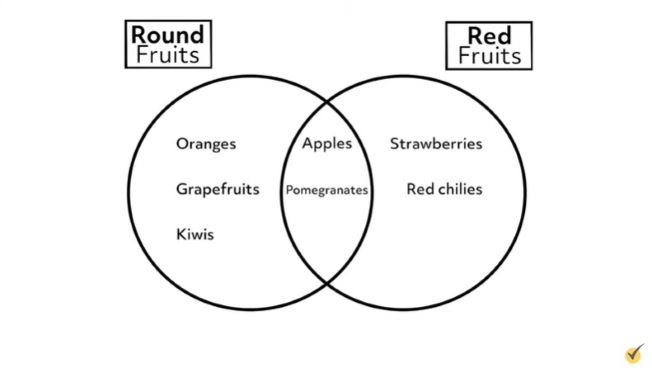
Here, we see that oranges, grapefruits, kiwis, apples, and pomegranates are all round fruits because they belong to the left circle. But because apples and pomegranates are in the overlapping area, they also belong to the set of red fruits, along with strawberries and red chilis.

Let’s look at another example of a Venn diagram. This one has two sets called A and B, each containing an assortment of numbers. Some of these numbers belong in both \(A\) and \(B\), while some other numbers do not belong to either set.

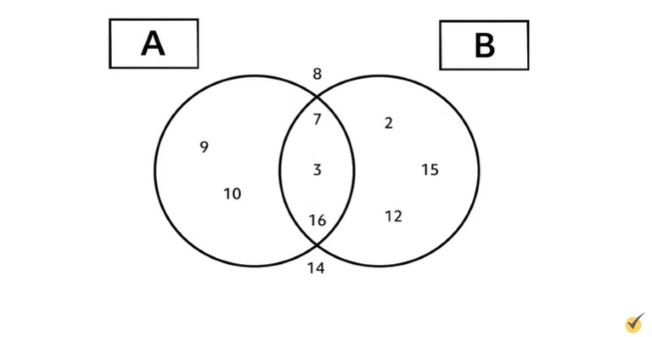
Based on this diagram, we can determine what numbers belong to the union, intersection, and complements of \(A\) and \(B\). Let’s try some of those now.

What is in \(A\cup B\)? \(A\) union \(B\) means to combine the sets. To find this, we need to collect all elements of \(A\) and all elements of \(B\). This means that \(A\cup B\) is going to contain 9, 10, 7, 3, 16, 2, 15, and 12.

What about \(A\cap B\)? \(A\) intersect \(B\) means to find what the sets have in common. To find this intersection, we must collect only the numbers which are in \(A\) and \(B\) simultaneously. That’s the middle section. This leaves us with 3, 7, and 16.

 
Let’s find complements now. What is in \(A’\)? This will be all numbers that aren’t in \(A\). So we’ll have 2, 15, and 12 from B, as well as 8 and 14 which are in neither \(A\) nor \(B\).

Similarly, \(B’\) will have all the numbers that aren’t in \(B\). This will include 9 and 10 from \(A\), and 8 and 14 from outside \(A\) and \(B\).

Something interesting to note is that if we take the intersection of \(A’\) and \(B’\), we get \(A’\cap B’={8,14}\). These are all of the numbers that are in neither \(A\) nor \(B\). So \(A’\cap B’\) is equivalent to the complement of \(A\cup B\).

A couple more things we can easily find from this Venn diagram are differences of sets. For example, \(A\) minus \(B\) is everything in \(A\) that isn’t in \(B\). So we won’t include 7, 3, or 16.

And \(B\) minus \(A\) is everything in \(B\) that isn’t in \(A\).

These differences between sets ignore elements that belong to the intersection of \(A\) and \(B\).

Alright, now that we’ve had some practice with using a Venn diagram to determine unions, intersections, complements, and differences between sets, let’s now apply this knowledge to a word problem!

Scientists in a pharmacy lab are conducting experiments with various solutions to determine which is best to use in a new antibiotic medication. Ten solutions were tested and labeled one through ten. Some were determined to be effective in fighting infection, while others were determined to disperse quickly in the patient’s body, according to these sets.

Create a Venn diagram to determine which solutions were both effective and quick, which were effective or quick, and which were effective but not quick.

Let’s start by drawing our Venn diagram. Label the left circle with the letter “\(E\)” for “effective” and the right circle with the letter “\(Q\)” for “quick.” From here, we can just write in where each of the solutions is supposed to go. Notice that the solutions 3 and 8 are in both \(E\) and \(Q\), so 3 and 8 will be written in the two circles’ overlap. 2 is in neither \(E\) nor \(Q\), so 2 will be written outside of the circles.

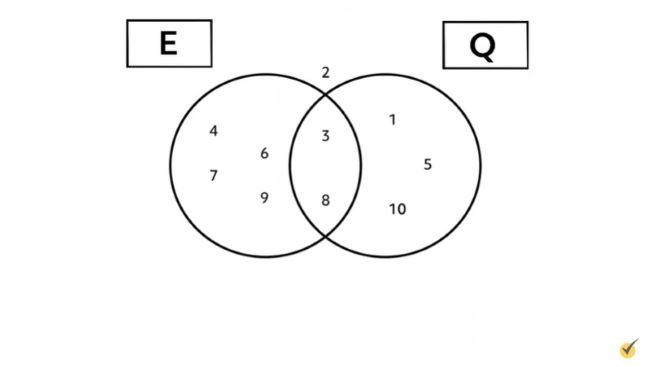
Now, the first question we want to answer is this: which solutions are both quick and effective? Let’s try to rephrase this in terms of set notation. Whenever you hear the word and, you should think “intersection.”

If a solution is considered both quick and effective, it must be both of those things simultaneously. In a Venn diagram, this means that it must lie in the overlap section and belong to the intersection of the two sets. So which solutions are in \(E\cap Q\)? With a quick look at our diagram, we can see that solutions 3 and 8 are the only ones in \(E\cap Q\).

The second question we are considering is, “Which solutions were effective or quick?” This question is deceptively similar to the previous but with one critical difference. Now, instead of looking for which solutions belong to both sets simultaneously, we want to find which solutions belong to set \(E\) or set \(Q\). When you hear the word or, you should think “union.”

In set theory problems, mathematicians consider the word “or” to indicate the element may belong to one set or the other, or to both—as long as an element belongs to at least one of the considered sets. So which solutions were effective or quick? Which elements are in \(E\cup Q\)? We can see from our Venn diagram that all solutions except for 2 were considered effective or quick.

The last question we want to answer is this: which solutions were effective but not quick? How do you think we would rephrase this in set notation? We want to consider the solutions that were effective, but without the ones that were also quick. We can write this as \(E∖Q\). This will be all of the effective solutions, except for 3 and 8, since those were also considered quick.

As we have seen, a Venn diagram can make set operation problems much easier to think about. In more complex examples, you may come across Venn diagrams which have three circles for three sets, or circles which are nested inside of another to represent subsets. In these examples, Venn diagrams are particularly helpful and can greatly simplify your work.

I hope this video was helpful. Thanks for watching, and happy studying!