
Hello! In this video you’ll learn what rounding and estimation are, how to do each of them, and see some first hand examples. Let’s get started!
Rounding and estimation both involve using approximations to simplify messy mathematics. They differ, however, in that rounding simplifies a messy number, while estimation simplifies a messy calculation.
For instance, suppose you buy a new riding lawn mower for exactly $3,184.29, but you tell your neighbor that it cost about $3,000. You have rounded the messier $3,184.29 to the simpler $3,000. On the other hand, suppose you need to buy 5 of these mowers for your lawn care business. To find the exact cost requires you to make the messy calculation 5×$3,184.29, but you can get a rough idea of the cost by instead using the estimate 5×$3,000=$15,000.
How to Round Numbers
So, how do we round a messy number? The basic plan is to replace the messy number with a nearby number that is easier to remember and easier to use in calculations. Here are the details.
When we write a number in our place-value number system, digits to the left are typically considered more significant than those to the right. To round a number, we first decide the last place—the least significant place—that we want to keep. We call this the rounding place, indicated by R. Every digit to the left of the rounding place is more significant (indicated by M) so we keep it. The next digit to the right (indicated by N) and all the remaining digits to the right are less significant (indicated by L), so we zero them out.

We must decide if we keep the digit in the rounding place (R) the same or increase it by 1. This will depend on the digit located one place to the right (N). If the next digit is 0 through 4, we keep the rounding digit unchanged. We call this rounding down.

If the next digit is 5 through 9, we increase the rounding digit by 1. We call this rounding up.

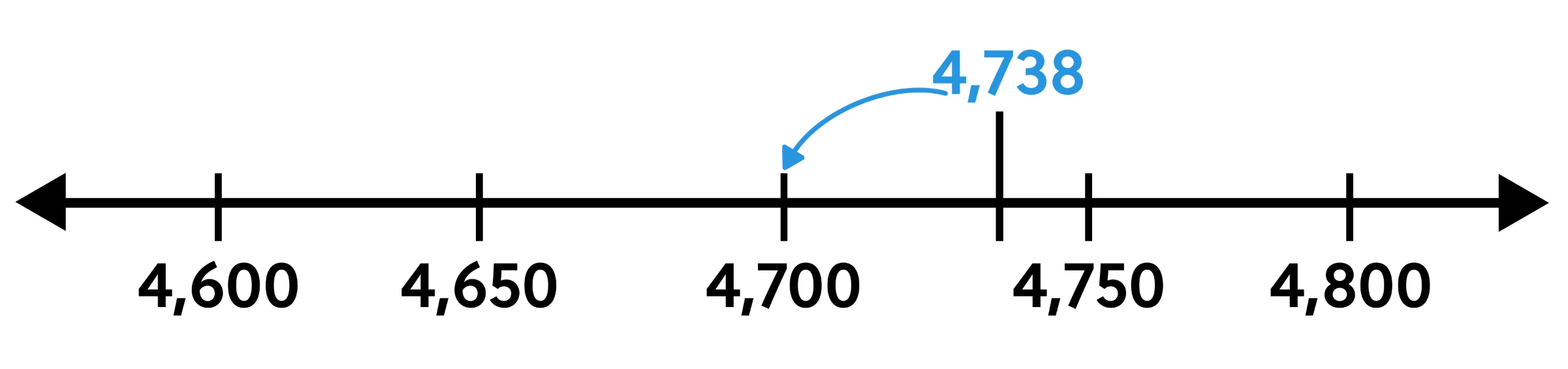
For example, suppose we want to round the number 4,738 to the hundreds place—we call this rounding to the nearest hundred. This means the 7 is in the rounding place because it is in the hundreds place. We keep the 4 because it is more significant. To decide what to do with the rounding digit, 7, itself, we look at the next digit, the 3. Since 3 is less than 5, we keep 7 unchanged. We zero out the 3 and 8 because they are less significant. So, 4,738 is rounded down to the nearest hundred giving us 4,700.
Now, suppose we want to round the number 4,738 to the thousands place—we call this rounding to the nearest thousand. This means the 4 is now in the rounding place. There are no more significant places, so we move on to deciding what to do with the rounding digit, 4. We look at the next digit, the 7. Since 7 is greater than or equal to 5, we round the 4 up by increasing it to 5. Then we zero out the 7, 3, and 8 because they are less significant. So, rounding 4,738 to the nearest thousand gives us 5,000.
Let’s put the previous examples on number lines, to help us visualize how rounding works. We rounded 4,738 to the nearest hundred, and got 4,700. If we plot 4,738 on a number line marked off by hundreds, 4,738 is closer to 4,700 than it is to 4,800.
In the next example, when we rounded 4,738 to the nearest thousand, we got 5,000. If we plot 4,738 on a number line marked off by thousands, we see that 4,738 is closer to 5,000 than 4,000.

By the way, if we ever want to round a number that is exactly halfway between two numbers on the number line, by convention we round up. This is the reason we round the rounding digit up whenever the next digit is 5.
What happens if we want to round a number to a fractional place—that is, to a place to the right of the decimal point? It turns out that the rules are exactly the same.
For instance, suppose we want to round the number 92.67381 to the nearest thousandth. Our rounding digit is the 3 in the thousandths place. We keep all the digits to the left of 3. Since the next digit, 8, is 5 or greater, we round the rounding digit up to 4. The numbers after 4 become 0. This gives us a rounded answer of 92.67400, which we can write as 92.674. This is sometimes called “rounding to three decimal places” instead of “rounding to the nearest thousandth.”
With enough practice you will be able to round most numbers almost instantly. There is one case, however, that often leads to confusion. What happens if your rounding digit is a 9, and you need to round it up? The answer is that you round 9 up to 10 by writing 0 in the rounding place and adding 1 to the place to the left.
For example, suppose you want to round 429.5 to the nearest whole number (that is, to the ones place). Your rounding digit is 9, so you keep the 4 and 2. Because the next digit is 6, you round the 9 up to 10, writing 0 in the ones place and adding 1 to the 2 in the tens place. Then you zero out the 5. This gives you a rounded value of 430.0 or just 430.
How to Estimate
Now let’s consider estimation. We estimate the result of a messy calculation by substituting a simpler calculation that gives a useful approximate answer. We often estimate by rounding some of the numbers in the messy calculation.
For example, suppose you need to buy 12 copies of a book that costs $18.76, and you want to know about how much the total will be. The exact answer is 12×$18.76, but that is hard to do in your head. So, you might estimate the total by rounding 12 down to 10 and calculating 10×$18.76=$187.60. Or you might estimate by rounding $18.76 up to $20 and calculating 12×$20=$240. Or you might even round both numbers, calculating 10×$20=$200. These are all legitimate ways to estimate the total. They are also all reasonably close to the exact value of 12×$18.76=$225.12.
The takeaway is that there may be several good ways to estimate the result of a calculation. An estimate is good as long as it is accurate enough to be useful.
Here is an example for you to practice. You are a teacher with a $500 budget to buy scientific calculators for a class of 37 students. You are on the phone with a vendor who will sell you scientific calculators for $9.49 each. Can you purchase the calculators at this price and stay within your budget? You need to make a quick estimate in your head to see if it is worth asking the vendor for more details. Estimate the cost of buying 37 calculators at this price. Pause the video while you make your estimate, and then continue the video to see how your answer compares to mine.
This is another example in which there are several good ways to make the estimate. You can round the 37 students up to 40 and the $9.49 price down to $9 to get an estimate of 40×$9=$360. You can also leave the 37 unrounded and round the $9.49 price up to $10 to get an estimate of 37×$10=$370. Rounding $9.49 up to $10 is not standard rounding; but $10 is a very simple number to work with, and it is still close enough to give you a useful estimate. In fact, rounding the price up has an added benefit. By rounding up, you guarantee that your estimate is an overestimate—a total higher than the exact answer.
Since the overestimate still falls within your $500 budget, you can be certain that the exact price of the calculators will be under $500. You can even take this approach one step further by rounding the class size of 37 up to 40 in addition to rounding the price up to $10 to get an overestimate of 40×$10=$400, also within the $500 budget. Now you know that you can afford this vendor’s price, and it is reasonable to continue the phone call to find out other details.
Keep in mind that this list of estimates is not exhaustive. You might come up with an estimate that is different but still valid and useful. And we should note that all these estimates are reasonably close to the exact value of 37×$9.49=$351.13.
In this lesson we learned that rounding is a way of simplifying numbers and estimation is a way of simplifying calculations. We round a number when we are more interested in the “big story” than the details. We estimate the value of a calculation when the extra labor of getting an exact answer is unnecessary, impossible, or meaningless.
The rounding and estimation guidelines in this video are widely used and will serve you well under most circumstances. But be aware that some circumstances and some jobs and fields of study call for different rounding and estimation rules. If you ever work in one of those fields, be sure to learn and follow its rules.
I hope this video was helpful. Thanks for watching, and happy studying!
Frequently Asked Questions
Q
How do you round to the nearest hundred?
A
Round a number to the nearest hundred by determining if the number in the tens place is greater than or equal to 5. If the tens place is greater than or equal to 5, increase the hundreds place by 1. If the tens place is less than 5, keep the hundreds place the same. Then, change every number after the hundreds place to a 0.
Ex. Round 6, 852 to the nearest hundred.
Look at the tens place. Since 5 ≥ 5, increase the hundreds place by 1 and replace every number after with a 0. 6,852 rounded to the nearest hundred is 6,900.
Q
How do you round to the nearest tenth?
A
Round to the nearest tenth by looking at the hundredth place. If it is greater than or equal to 5, round the tenth place up one digit. If it is less than 5, keep the tenths place the same. Don’t write any numbers after the tenths place.
Ex. Round 16.423 to the nearest tenth.
Find the hundredths place: 2. 2 is less than 5, so round down (tenths place stays the same). Only write up to the tenths place. 16.423 rounds to 16.4
Q
How do you round decimals?
A
Round decimals the same way you round non-decimal numbers. Check the number in the place value one below the one you are rounding to. If it is greater than or equal to 5, round up. If it is less than 5, round down. Then, only write the numbers until you reach the place you are rounding to.
Ex. Round 8.715 to the nearest whole number.
Since 7 is greater than 5, round up. 8.715 rounds to 9.
Ex. Round 63.271 to the nearest hundredth.
Since 1 is less than 5, round down. 63.271 rounds to 63.27.
Rounding Practice Problems
Which of the following is 1,566.836 rounded to the nearest hundredths place?
The correct answer is C: 1,566.84. First of all, we know that the “hundredths place” is the second digit on the right of the decimal; so we know that the 3 is our round-off digit. The digit on the right-side of the 3 is greater than or equal to 5, so we must round up that 3 to a 4 and drop the final digit (drop the 6 that’s in the thousandths place).
Which of the following is two hundred seventy-four, and sixty-one hundredths rounded to the nearest tenths place?
The correct answer is B: 274.6. The first step is to write “two hundred seventy-four, and sixty-one hundredths” in numeric form: 274.61 . Now, since our rounding-off digit’s place value is the tenths place, we know that we will either round up the 6 or leave it alone (but no matter what, we will be dropping the 1). Because 1 is less than 5, we do not need to round that 6 up.
Consider the number 93.84659 , and you’ve been told to round this to the nearest thousandths place. What is your rounding-off digit?
The digit that is in the thousandths place (three “spaces” to the right of the decimal) is 6. Because the digit to the right of it is 5, we know that we would round up the 6, and we’d end up with the number 93.847 .
Which of the following is 25.832344 rounded to the nearest thousandths place?
The correct answer is C: 25.832. The 2 in the thousandths place is our rounding-off digit, and the digit to the right of it is 3. Since 3 is less than 5, we leave that 2 alone and drop any remaining digits (in other words: we truncate the number to the thousandths place).
Jenny pulls up to the nearest gas station, Oval J, to fill up her gas tank. A gallon of Unleaded gasoline costs $2.849, and she wants to fill her car with 11 more gallons of fuel. How much money will she spend on filling up her gas tank? (Hint: wait to round! Rounding will be the very last step in your calculation.)
The correct answer is D: $31.34. While it’s tempting to round up the gasoline’s unit price ($2.849 per gallon) and then multiply $2.85 by 11 gal, that is not how we’d calculate our final answer! Actually, we first multiply 2.849 by 11 to find that Jenny would pay $31.339 for 11 gallons. This looks strange, though, right? We normally only pay amounts that end in the hundredths place (think: $1.00, $2.50, and so on), so we need to round $31.339 to the nearest hundredths place. Our rounding-off digit is the rightmost 3, and the digit to the right of that is 9. Since 9 is greater than or equal to 5, we round up our rounding-off digit to end up with the amount $31.34.
