
Most of us learned how to draw a circle in math class using a compass. All we needed to know was where to put the center of the circle and the measure of the radius to set on the compass. Then we held the compass steady at the center and rotated the pencil part all the way around to draw our circle. If we drew it on graph paper and looked closely, we could probably find a few specific points on our circle.
But what if we don’t have a compass? Or graph paper? Or even the radius of the circle? What if we are only given the center of the circle and one point on the circle? Can we find other points on the circle?
The answer, of course, is yes. And that’s what we’re going to do today.
Finding Points on a Circle
Let’s start by looking at the equation of a circle:
Wow that’s a lot of variables! The \(x\) and the \(y\) are pretty standard, but the others might not be familiar. The \(h\) and the \(k\) together make the center of the circle at the point \((h,k)\). The \(r\) is the radius of the circle.
So if we have a circle with a center at the point \((2,3)\) and a radius of 5, our equation would look like this:
We simply plug in the values for \(h\) and \(k\), and then square the radius for the right side of the equation. Be careful when \(h\) and \(k\) are negative, though. For instance, if the radius is 4 and the center of the circle is at \((-4,-5)\) and we substitute into our equation, we have to deal with subtracting negatives:
Those two negative signs in a row cancel and we end up with:
When the center of the circle is at the point \((0,0)\), also known as the origin, our equation gets simpler:
Simple, right? But we’ve gotten a bit carried away. Let’s get back to our problem. If we’re given the center of a circle and 1 other point, can we find 3 other points on a circle?
Let’s do an actual problem to see how we should get this done.
Find at least 3 other points on a circle that has a point at \((2,6)\) and its center at \((-2,3)\).
So our point is gonna be at \((2,6)\). And our center is at \((-2,3)\).
The first thing we need to do is find the radius of the circle. We can do this by plugging in everything we know into our equation for a circle. Since we know the center is \((-2,3)\), we know that \(h=-2\) and \(k=3\). Since we know a point on our circle, we can use \(x=2\) and \(y=6\). We plug it all in and it looks like this.
So the formula for a circle is:
So our \(x\) and \(y\) comes from our point we were given, and our center is our \(h\) and \(k\).
We deal with our subtracting a negative problem to get this. \(2-(-2)\) is the same as \(2+2\), so we just replace that minus a negative with a plus sign. And then everything else stays the same.
Then we evaluate what’s in each set of parentheses. \(2+2=4\), so we have :
We apply our exponents. \(4^2=16\) and \(3^2=9\).
And then we’re gonna add them and solve for \(r\). So, \(16+9=25\).
We’ll square root both sides and get that \(r=5\).
Now what? How can we use this information to find more points on our circle? We’re going to use a different kind of compass to do that! Let’s get out a piece of graph paper and plot what we know so far.
Since we know our radius, we can travel north, south, east, and west from that point exactly 5 units to find more points! Moving along the compass points is easy on our graph paper, and since the radius is the distance from the center of the circle to all the points on the circle, we know we’ll end up on our circle when we travel 5 units.
Look at all those points we found! Going north five units we found \((-2,8)\), going west we found \((-7,3)\), going south we found \((-2,-2)\), and going east we found \((3,3)\)! 4 points! One more than the problem asked us to find.
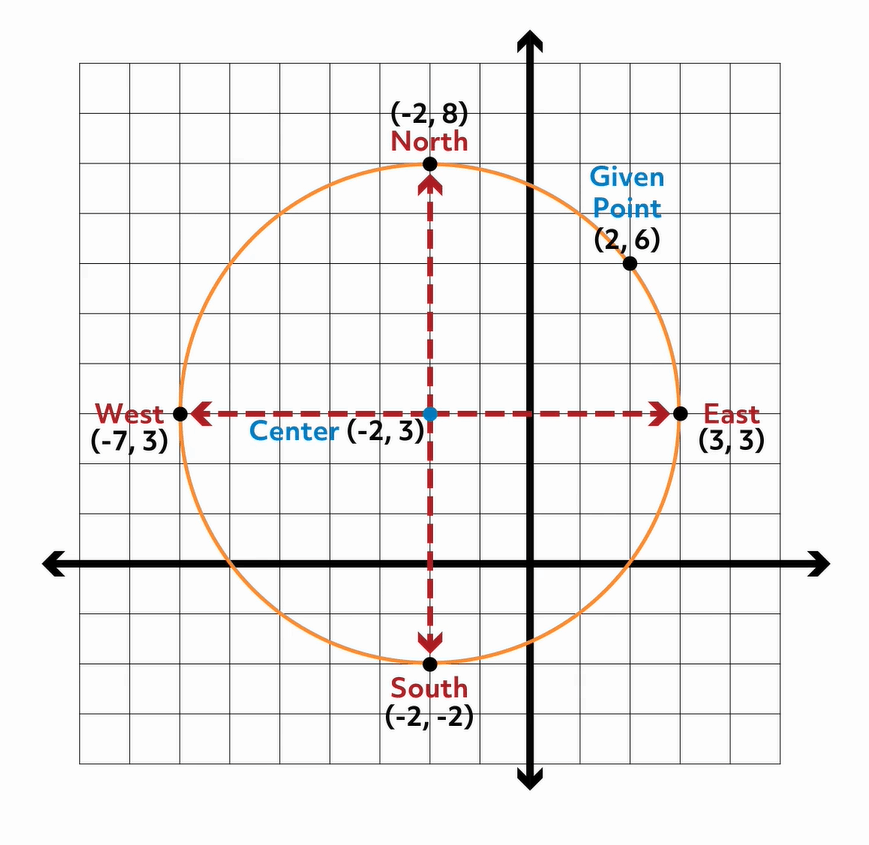
And we’re not done yet! We can find even more points if we want, since the given point isn’t one of our 4 “compass points.” If we look to see how far over and up that point is from the center, we can find more points that are the same L-shaped distance away. Here we can see that \((2,6)\) is 4 units to the right and 3 units up from the center of the circle. So I can draw L-shapes from the center that move 4 units left or right and then 3 units up and down to find more points.
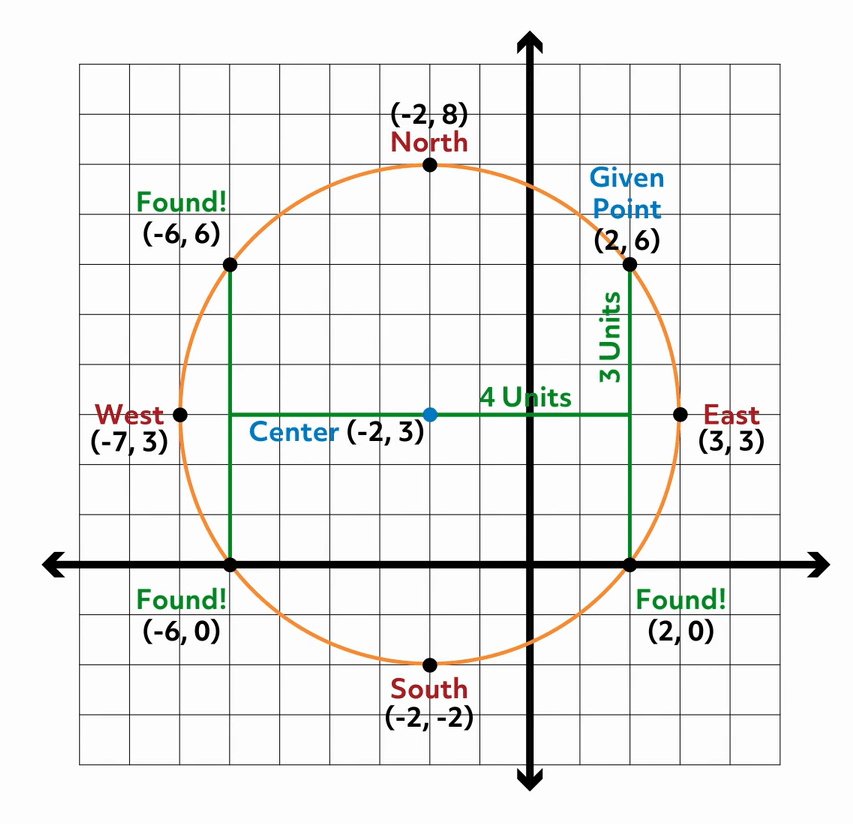
We found 3 more! On the left (or west) side we found \((-6,6)\) and \((-6,0)\) and below our given point we found \((2,0)\). Altogether we now have 8 points on our circle including the given one! And if we’re willing to do some heavier math, we can find any of the infinite number of points on our circle. Since we’re on such a roll, let’s try that too!
First we need to establish our domain so we know what \(x\)-values we can pick. The leftmost \(x\)-value on our circle is our “west” point at -7. Our rightmost point is our “east” point at +3. So our domain is \(x\geq -7\) and \(x\leq 3\).
So we can pick any \(x\)-value from -7 to 3 to find its corresponding \(y\)-values on the circle. Yes, it’s plural because there will be 2.
So let’s pick \(x=-4\) from our domain. Now all we have to do is plug that into our equation for this circle and solve for \(y\).
So we’re using the \(x\)-value -4. And remember, our center is at the point \((-2,3)\). So now all we’re gonna do is plug that into our equation for the circle. So remember, that’s:
So our \(x\)-value is -4, minus \(h\) is -2, plus \(y\) (we don’t know what that is, that’s what we’re trying to solve for) minus \(k\), which is 3, squared, and we forgot to write this, but our \(r\), remember from earlier is 5, so is equal to 5 squared.
So \(-4-(-2)\), that’s the same as saying \(-4+2\), so let’s rewrite it that way.
Then we’ll simplify \(-4+2\) to \(-2\), so:
And now we’re gonna simplify our exponents. \((-2)^2=4\) plus (we’ll leave this part alone for right now, we’ll come back to that later) \((y-3)^2\) equals, \(5^2=5\).
Now we’ll subtract 4 from both sides. This gives us:
And we’ll take the square root of both sides. That leaves us with:
And all we have to do is add 3 to both sides. So our answers are:
So our two values are \(\sqrt{21}+3\) and \(-\sqrt{21}+3\). If we’re plotting those points on a graph, we can estimate their value by using a calculator to find that our \(y\)-values are approximately 7.58 and -1.58. So we can graph those too!
Now we’re up to 10 points on our circle! Can you find any more? Pause this video now and try. The answer for all the integer values of \(x\) will appear shortly after unpausing.
Here are the other points on the circle with integer \(x\)-values:
\((-3,2\sqrt{6}+3)(-3,-2\sqrt{6}+3)\)
\((-1,2\sqrt{6}+3)(-1,-2\sqrt{6}+3)\)
\((0,\sqrt{21}+3)(0,-\sqrt{21}+3)\)
\((1,-1)(1,7)\)
I hope this video over finding points on a circle was helpful. Thanks for watching, and happy studying!
Points on a Circle Practice Questions
Which of the following sets of points are on a circle that has its center at \((3,6)\) and a radius of 13 units?
The equation of a circle in standard form is \((x-h)^2+(y-k)^2=r^2\), where \((h,k)\) is the center, and \(r\) is the radius of the circle. The ordered pair \((x,y)\) represents any point on the circle. Substituting our center and radius into the equation of a circle, we have:
\((x-3)^2+(y-6)^2=13^2\)
\((x-3)^2+(y-6)^2=169\)
An ordered pair \((x,y)\) is a point on the circle if it satisfies the equation of the circle. Substituting \((-2,-6)\) into the equation of the circle, we get:
\((-2-3)^2+(-6-6)^2=169\)
\((-5)^2+(-12)^2=169\)
\(25+144=169\)
\(169=169\)
Since the ordered pair produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is a point on the circle.
Substituting \((8,18)\) into our equation, we get:
\((8-3)^2+(18-6)^2=169\)
\((5)^2+(12)^2=169\)
\(25+144=169\)
\(169=169\)
Since the ordered pair \((8,18)\) produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is also a point on the circle.
Which of the following set of points are on a circle that has its center at \((-2,4)\) and contains the point \((-2,0)\)?
Since we are given the center and a point on the circle, we can find its radius.
The equation of a circle in standard form is \((x-h)^2+(y-k)^2=r^2\), where \((h,k)\) is the center, and \(r\) is the radius of the circle. The ordered pair \((x,y)\) represents any point on the circle.
Substituting our center \((-2,4)\) into the equation of the circle, we have:
\((x-(-2))^2+(y-4)^2=r^2\)
\((x+2)^2+(y-4)^2=r^2\)
Now entering the given point \((-2,0)\) into the equation for the circle, we have:
\((-2+2)^2+(0-4)^2=r^2\)
\((-2+2)^2+(-4)^2=r^2\)
\((0)^2+(-4)^2=r^2\)
\(16=r^2\)
\(\sqrt{16}=\sqrt{r^2}\)
\(r=4\)
While \(r=\pm4\), we only use 4 since the radius has a non-negative length.
Substituting our center and radius into the equation of a circle, we have:
\((x+2)^2+(y-4)^2=4^2\)
\((x+2)^2+(y-4)^2=16\)
In this case, since the given point is directly below the center of the circle, we could also find the radius by counting 4 units from the center to the given point (or 4 units from the given point to the center) as shown in the figure below.
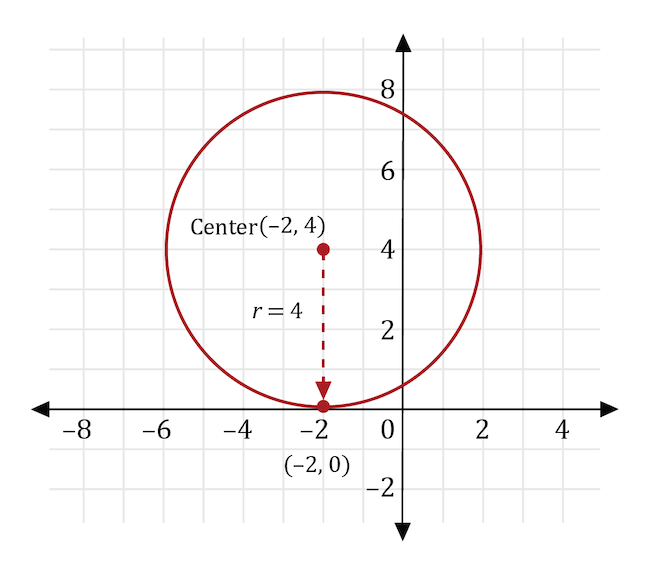
An ordered pair \((x,y)\) is a point on the circle if it satisfies the equation of the circle. Substituting \((0,4-2\sqrt{3})\) into the equation of the circle, we get:
\((0+2)^2+(4-2\sqrt{3}-4)^2=16\)
\((2)^2+(-2\sqrt{3})^2=16\)
\(4+4\cdot3=16\)
\(4+12=16\)
\(16=16\)
Since the ordered pair produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is a point on the circle.
Substituting \((0,4+2\sqrt{3})\) into the equation of the circle, we get:
\((0+2)^2+(4+2\sqrt{3}-4)^2=16\)
\((2)^2+(2\sqrt{3})^2=16\)
\(4+4\cdot3=16\)
\(4+12=16\)
\(16=16\)
Since the ordered pair \((0,4+2\sqrt{3})\) produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is also a point on the circle.
Which are the leftmost and rightmost points that are on a circle that has a center at \((4,-1)\) and contains the point \((8,2)\)?
Since we are given the center and a point on the circle, we can find its radius. Then we can use the radius to find the circle’s leftmost and rightmost points.
The equation of a circle in standard form is \((x-h)^2+(y-k)^2=r^2\), where \((h,k)\) is the center, and \(r\) is the radius of the circle. The ordered pair \((x,y)\) represents any point on the circle.
Substituting our center \((4,-1)\) into the equation of the circle, we have:
\((x-4)^2+(y-(-1))^2=r^2\)
\((x-4)^2+(y+1)^2=r^2\)>/p>
Now entering the given point \((8,2)\) into the equation for the circle, we have:
\((8-4)^2+(2+1)^2=r^2\)
\((4)^2+(3)^2=r^2\)
\(16+9=r^2\)
\(25=r^2\)
\(\sqrt{25}=\sqrt{r^2}\)
\(r=5\)
While \(r=\pm5\), we only use 5 since the radius has a non-negative length.
On the coordinate plane, we can use the value of \(r\) to count a radius length of 5 units horizontally to the left and right (or west and east) from the center of the circle to find the furthest most left and right points, respectively.
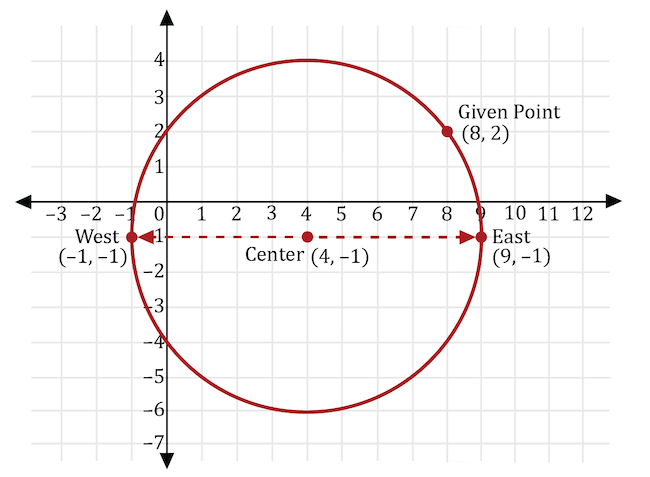
Counting a radius length of 5 units to the west from the center produces the leftmost point of \((-1,-1)\) on the circle. Counting a radius length of 5 units to the east from the center produces rightmost point of \((9,-1)\).
Counting a radius length of 5 units from the center to the west and east always produces the leftmost and rightmost points on the circle. Below are 2 additional points that are graphed on the circle. While both points are also 5 units from the center, notice that neither are the leftmost or rightmost points.
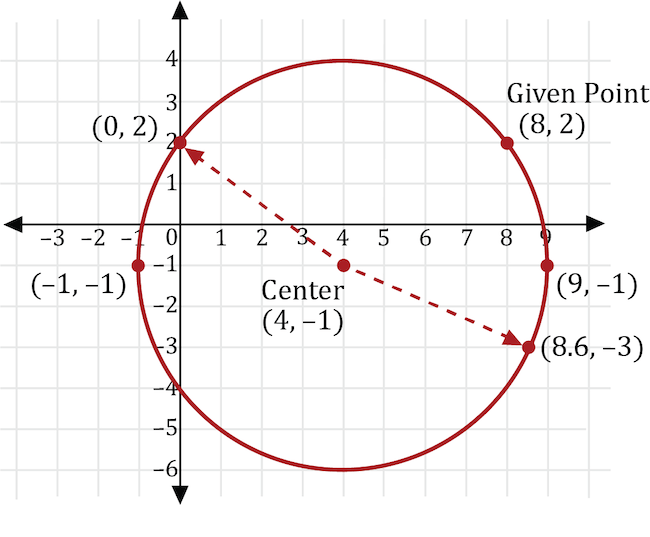
You tie your pet with a rope to a stake that is mounted to the ground. When the rope is fully extended, your pet can walk a circular path around the stake. If the rope is 10 feet long and the stake is mounted at the origin of the coordinate plane, which of the following points are on the path that your pet takes?
The equation of a circle in standard form is \((x-h)^2+(y-k)^2=r^2\), where \((h,k)\) is the center of the circle, and \(r\) is the radius of the circle. The ordered pair \((x,y)\) represents any point on the circle. Since the stake is at the origin of the coordinate plane, it is a point that has coordinates \((0,0)\). When the rope is fully extended, it forms the radius for the circular path your pet walks, so \(r=10\). Substituting our center and radius into the equation of a circle, we have:
\((x-0)^2+(y-0)^2=10^2\)
\(x^2+y^2=100\)
An ordered pair (x,y) is a point on the circle if it satisfies the equation of the circle. Substituting (-8,6) into the equation of the circle, we get:
\((-8)^2+(6)^2=100\)
\(64+36=100\)
\(100=100\)
Since the ordered pair produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is a point on the circle.
Substituting \((6,8)\) into our equation, we get:
\((6)^2+(8)^2=100\)
\(36+64=100\)
\(100=100\)
Since the ordered pair \((6,8)\) produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is also a point on the circle.
The ends of the spokes for a bicycle tire are attached to the center of the tire’s hub and its rim. The tire contains 20 spokes. If the hub is centered at the origin of the coordinate plane and the end of one of its spokes is at the point \((6,-2)\) in the coordinate plane, on which set of points could the ends of two of the other 19 spokes lie?

Since the center of the hub of the bicycle is at the origin of the coordinate plane, it is a point that has coordinates \((0,0)\). We can use the origin and the given point on the circle to find its radius.
The equation of a circle in standard form is \((x-h)^2+(y-k)^2=r^2\), where \((h,k)\) is the center of the circle, and \(r\) is the radius of the circle. The ordered pair \((x,y)\) represents any point on the circle. Substituting our center \((0,0)\) into the equation of the circle, we have:
\((x-0)^2+(y-0)^2=r^2\)
\(x^2+y^2=r^2\)
Now entering the given point \((6,-2)\) into the equation for the circle, we have:
\((6)^2+(-2)^2=r^2\)
\(36+4=r^2\)
\(\sqrt{40}=\sqrt{r^2}\)
\(r=\sqrt{40}\) or \(2\sqrt{10}\)
While \(r=\pm2\sqrt{10}\), we only use \(2\sqrt{10}\) since the radius has a non-negative length.
Substituting our center and radius into the equation, we have:
\(x^2+y^2=(2\sqrt{10})^2\)
\(x^2+y^2=4\cdot10\)
\(x^2+y^2=40\)
An ordered pair \((x,y)\) is a point on the circle if it satisfies the equation of the circle. Substituting \((-2,6)\) into the equation of the circle, we get:
\(x^2+y^2=40\)
\((-2)^2+( 6)^2=40\)
\(4+36=40\)
\(40=40\)
Since the ordered pair produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is a point on the circle.
Substituting \((5,\sqrt{15})\) into the equation of the circle, we get:
\((5)^2+(\sqrt{15})^2=40\)
\(25+15=40\)
\(40=40\)
Since the ordered pair \((5,\sqrt{15})\) produces a true statement when substituting it into the equation of the circle, it satisfies the equation, so it is also a point on the circle.
