A circle is the set of all points on a plane that are equidistant from a center point. The radius of a circle is a line segment that has its endpoints on the center and any point on the circumference of the circle.
Take a look at this circle on the coordinate plane:
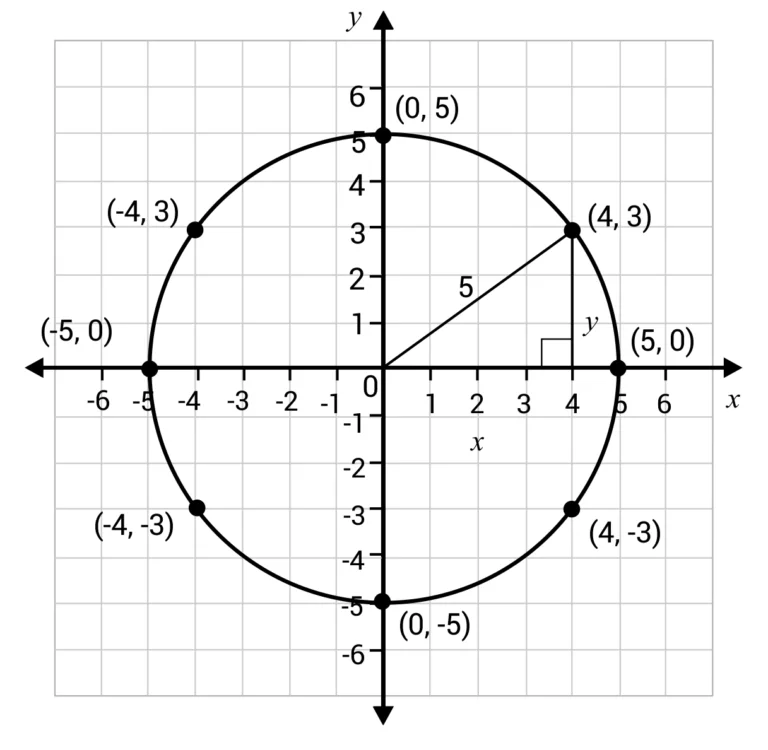
The circle has a radius of 5 units and its center point is at \((0,0)\). We can create a right triangle by drawing a perpendicular line from the point on the circle to the x-axis. Since this is a Pythagorean Triple, it is easy to see that \(4^2+3^2=5^2\). The table shows some other points on the circle, which can help us see the pattern, \(x^2+y^2=r^2\).
| \(x\) | \(y\) | \(x^2+y^2\) |
| \(4\) | \(3\) | \(4^2+3^2=25\) |
| \(0\) | \(5\) | \(0^2+5^2=25\) |
| \(5\) | \(0\) | \(5^2+0^2=25\) |
| \(-4\) | \(3\) | \((-4)^2+3^2=25\) |
| \(-5\) | \(0\) | \((-5)^2+0^2=25\) |
| \(-4\) | \(-3\) | \((-4)^2+(-3)^2=25\) |
| \(0\) | \(-5\) | \(0^2+(-5)^2=25\) |
| \(4\) | \(-3\) | \(4^2+(-3)^2=25\) |
This pattern only works if the center of the circle is at \((0,0)\). Here is a circle that has its center at \((h,k)\), which makes the side lengths of the legs \(x–h\) and \(y–k\) and the hypotenuse of the triangle the radius of the circle, r. Since we already proved that \(x^2+y^2=r^2\), we can conclude \((x–h)^2+(y–k)^2=r^2\), we call this the center radius form of the circle equation, because we can easily pick out the center and radius of the circle when the equation is in this form.
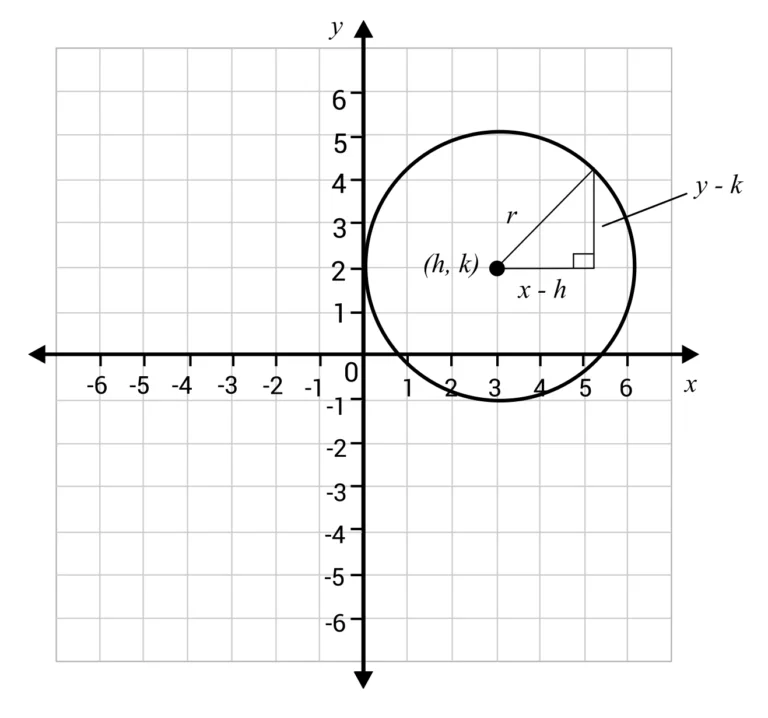
For example, the equation of a circle with center \((2,5)\) and radius 7 would be written as \((x–2)^+(y–5)^=7^2\).
Another form of the circle equation is called the general form and is written as \(ax^2+by^2+cx+dy+e=0\).
To change the equation from center radius form to general form, you must expand and simplify the equation.
We will use the above example. Write the equation of the circle, \((x–2)^2+(y –5)^2=7^2\), in general form:
\((x–2)^2+(y–5)^2=7^2\)
Write in expanded form:
\((x–2)(x–2)+(y–5)(y–5)=49\)
Expand:
\(x^2–2x–2x+4+y^2-5y–5y+25–49=0\)
Combine like terms:
\(x^2+y^2–4x–10y–20=0\)
To change the equation from general form to center radius form, you have to apply a method called completing the square.
Write the equation of the circle \(2x^2+2y^2-4x-16y-38=0\) in center radius form.
\(2x^2+2y^2-4x-16y=38\)
Step 2: Put the terms with \(x\) together and the terms with \(y\) together.
\(2x^2–4x+2y^2–16y=38\)
Step 3: Divide each term by the leading coefficient.
\(x^2–2x+y^2–8y=19\)
Step 4: Rewrite with parentheses and spaces for the third term in the polynomial.
\((x^2–2x)+(y^2–8y)=19\)
Step 5: To complete the square, take the coefficient of \(x\) and \(y\), divide it by 2, then square it to get the third term in the polynomial. Add these numbers to both the left and the right side of the equation.
\((-2÷2)^2=1(-8÷2)^2=16\)
\((x^2–4x+1)+(y^2–6y+16)=19+1+16\)
Step 6: Simplify by factoring:
\((x–1)^2+(y–4)^2=36\)

Circle Equations Sample Questions
Which variables represent the center and radius of a circle in the following equation?
\((x-h)^2+(y-k)^2=r^2\)
The equation \((x-h)^2+(y-k)^2=r^2\) is in center radius form, also known as standard form. This allows the center and radius of the circle to be easily identified. The center is always \((h,k)\) and the radius is always \(r\).
Is the following equation in general form or center radius form?
\(x^2-6x+y^2+8y+5=0\)
The equation of a circle in general form is:
\(ax^2+by^2+cx+dy+e=0\)
The equation of a circle in center radius form is:
\((x-h)^2+(y-k)^2=r^2\)
Write the following equation in general form:
\((x-8)^2+(y-(-2))^2=5^2\)
The equation \((x-8)^2+(y-(-2))^2=5^2\) is in center radius form. In order to write the equation in general form, we need to do a bit of algebraic manipulation. Essentially, we want to expand each set of parentheses and then simplify the result.
Original equation: \((x-8)^2+(y-(-2))^2=5^2\)
Step 1: Rewrite each set of parentheses in expanded form, and write \(5^2\) as simply 25.
\((x-8)(x-8)+(y+2)(y+2)=25\)
Step 2: Expand each set of parentheses. The equation now becomes:
\(x^2-16x+64+y^2+4y+4=25\)
Step 3: Simplify. Combine all like-terms. Move all of the terms to the left side so the equation is set equal to zero.
\(x^2+y^2-16x+4y+43=0\)
Write the equation of a circle with a center point at \((4,8)\) and a radius of 12. Write the equation in center radius form.
The equation of a circle in center radius form is:
\((x-h)^2+(y-k)^2=r^2\)
The center point of the circle is \((4,8)\) so plug in 4 for \(h\) and 8 for \(k\). The variable \(r\) represents the radius, so plug in 12 for \(r\). \(r^2=144\), so the final equation in center radius form would be: \((x-4)^2+(y-8)^2=144\).
Complete the square to find the center and radius of the circle having the following equation:
\(x^2+y^2-8x+4y+11=0\)
Step 1: Move the “loose” number to the right side. That is, take away 11 from both sides:
\(x^2+y^2-8x+4y=-11\)
Step 2: Group the variables with parentheses. Put the \(x\)-variables by the \(x\)-variables, and the \(y\)-variables by the \(y\)-variables. Now we have:
\((x^2-8x)+(y^2+4y)=-11\)
Step 3: Complete the square for the \(x\)’s and the \(y\)’s (this is called adding the squaring term). Take the \(x\)-term coefficient, multiply it by 12, and then square it. Then, add it to both sides of the equation and repeat the process for the \(y\)-term coefficient. Here is what the process looks like:
The \(x\)-term coefficient is -8. Multiply -8 by \(\frac{1}{2}\), which is -4. Square -4 to get 16, then add 16 to both sides of the equation. The \(y\)-term coefficient is 4. Multiply 4 by \(\frac{1}{2}\) to get 2. Square 2 to get 4, and add 4 to both sides of the equation.
The result is \((x^2-8x+16)+(y^2+4y+4)=-11+16+4\)
Step 4: Factor these two large sets of parentheses down to binomials squared.
\((x^2-8x+16)\) becomes \((x-4)^2\)
\((y^2+4y+4)\) becomes \((y+2)^2\)
The right side of the equation simplifies to 9, so the equation now looks like this:
\((x-4)^2+(y+2)^2=9\)
Now the equation is in center radius form. The center of the circle is \((h,k)\), so the center point is at \((4,-2)\). \(r^2\) is 9, so the radius is 3.
