Law of Sines
Hi, welcome to this video about the Law of Sines!
If you recall, the Pythagorean theorem is useful for finding the missing side of a right triangle. Our topic today, the Law of Sines, can be used to help us find the missing side or angle inside any kind of triangle if we have enough information.
Here’s a triangle we’ll call ABC, with the sides a, b, and c:
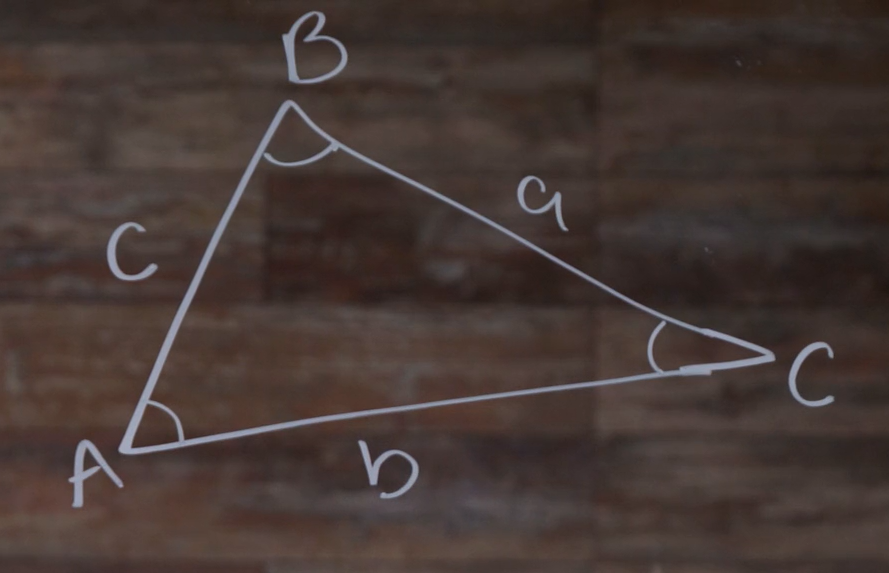
Notice how \(\angle A\) is opposite side a, and how it’s the same for B and C.
The Law of Sines tells us that:
\(\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}\)What this means is that the ratios of the length of a side and the sine of its opposite angle are in proportion to the ratio for the other angles and their opposite side.
Let’s jump right in and use it to find a missing side of a triangle:
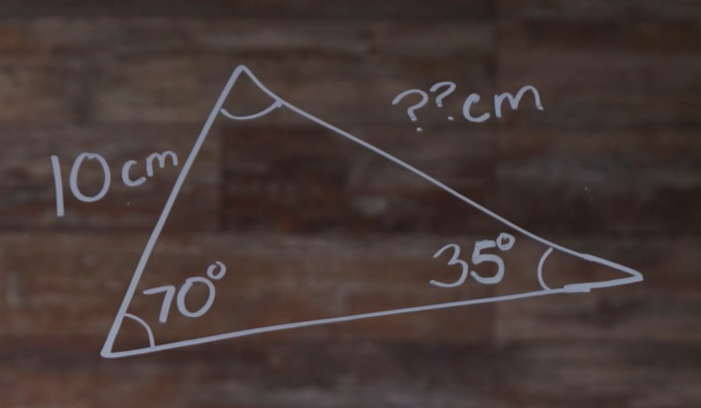
The first thing we need to do is check to see if we have enough information to find the missing side. We need one angle and its opposite side length, which we have. We can make one complete ratio using the 35° angle and the 10 cm opposite side. Now we just need the angle opposite the missing side, which we have. It’s 70°. That’s all we need to find the missing side.
It doesn’t matter which side we call a and which side we call b. Let’s call our missing side a and its opposite \(\angle A\). And we’ll have that as b and the opposite \(\angle B\). In this case, we don’t need side c or \(\angle C\) at all.
But the Law of Sines doesn’t have angles in it; instead it has the sine of angles. So we need to use a calculator and find the SIN key. Type in the angle and then hit SIN and you’ll end up with a long decimal for both of our angles:
\(\frac{a}{0.93969}=\frac{10\text{ cm}}{0.57657}\)Now we have a simple proportion to solve. We just need to solve for a:
\({(0.93969)}\frac{a}{0.93969}=\frac{10\text{ cm}}{0.57657}(0.93969)\) \(a\approx 16.4\text{ cm}\)We can do a quick mental check that can sometimes catch errors. The larger angle should have a longer side opposite it, and in this case it does (\(16.4\text{ cm} >10\text{ cm}\)).
But that’s not all. We can also use the Law of Sines to find a missing angle in a triangle. Here’s a sample problem:
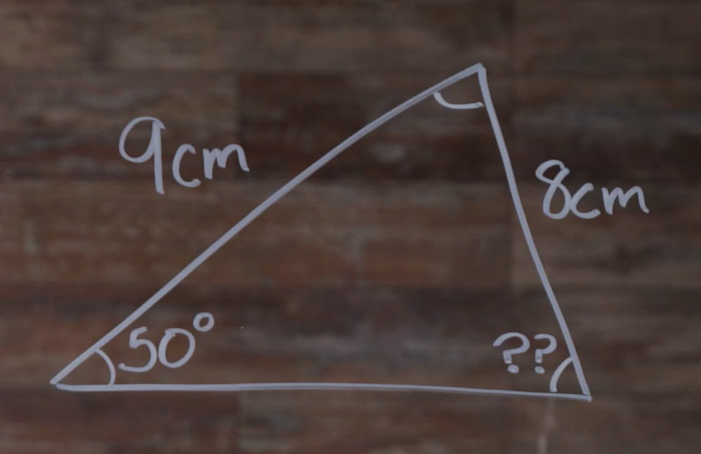
We have two sides and one of their opposite angles, so let’s find the missing opposite angle. When using Law of Sines to find an angle it’s a bit easier if we flip all the ratios, like this:
\(\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\)Now let’s fill it in. Remember that we only need two of the ratios, and it’s not important which is \(\angle A\) or side a, as long as the sine of the angle and its opposite side are together in a ratio. Once again, let’s keep our missing part on the left side and call it A. We have:
\(\frac{\sin{A}}{9\text{ cm}}=\frac{\sin{50^{\circ}}}{8\text{ cm}}\)Now we just solve it by multiplying both sides by 9 cm.
\(\sin{A}=0.86179999\)Now all we have to do is find \(\angle A\) instead of \(\sin{A}\). We do this by using the inverse SIN function of your calculator, which is usually written as SINr1 and can often be accessed by using the 2nd button before hitting SIN. Taking the inverse SIN of 0.8617999 gives us an angle of approximately 59.5 degrees. That’s all there is to it!
Thanks for watching and happy studying!
Law of Sines Practice Questions
Solve for x.
13.21
25.09
28.75
31.17
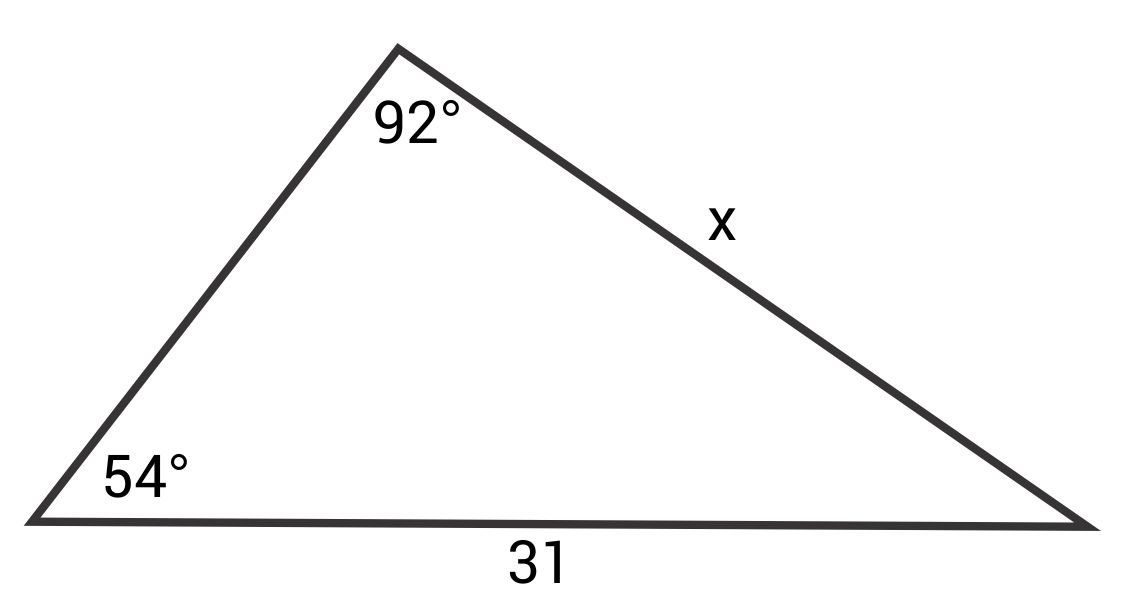
The correct answer is 25.09. The Law of Sines states:
\(\frac{\text{sin }a}{A}=\frac{\text{sin }b}{B}=\frac{\text{sin }c}{C}\)
Filling in the information from this triangle gives:
\(\frac{\text{sin }92°}{31}=\frac{\text{sin }54°}{x}\)
Manipulate to isolate x.
\(x\text{ sin }92°=31\text{ sin }54°\)
\(x=\frac{31\text{ sin }54°}{\text{sin }92°}\)
\(x≈25.09\)
Solve for x.
25.08
13.14
29.17
18.52
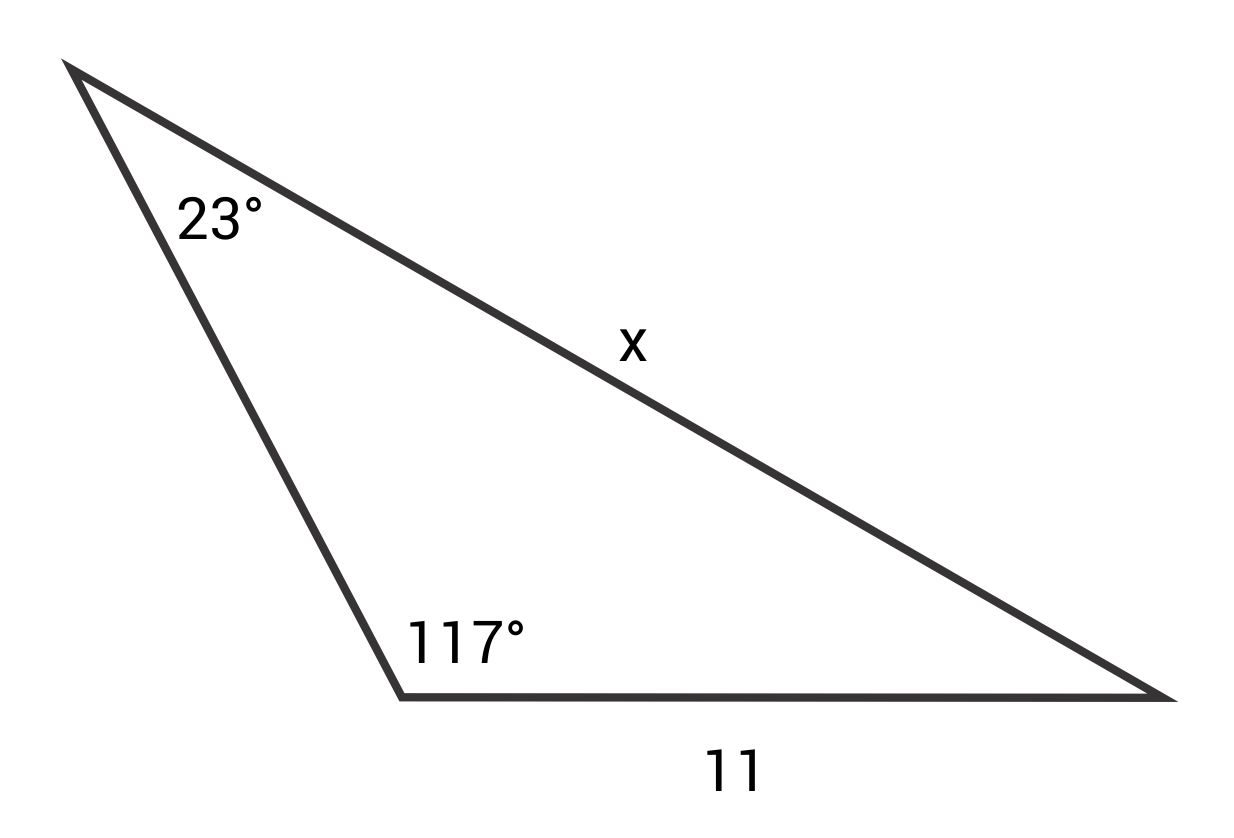
The correct answer is 25.08. The Law of Sines states:
\(\frac{\text{sin }a}{A}=\frac{\text{sin }b}{B}=\frac{\text{sin }c}{C}\)
Filling in the information from this triangle gives:
\(\frac{\text{sin }23°}{11}=\frac{\text{sin }117°}{x}\)
Manipulate to solve for x.
\(x\text{ sin }23°=11\text{ sin }117°\)
\(x=\frac{11\text{ sin }117°}{\text{sin }23°}\)
\(x≈25.08\)
Solve for x.
83.92°
82.13°
49.17°
43.05°
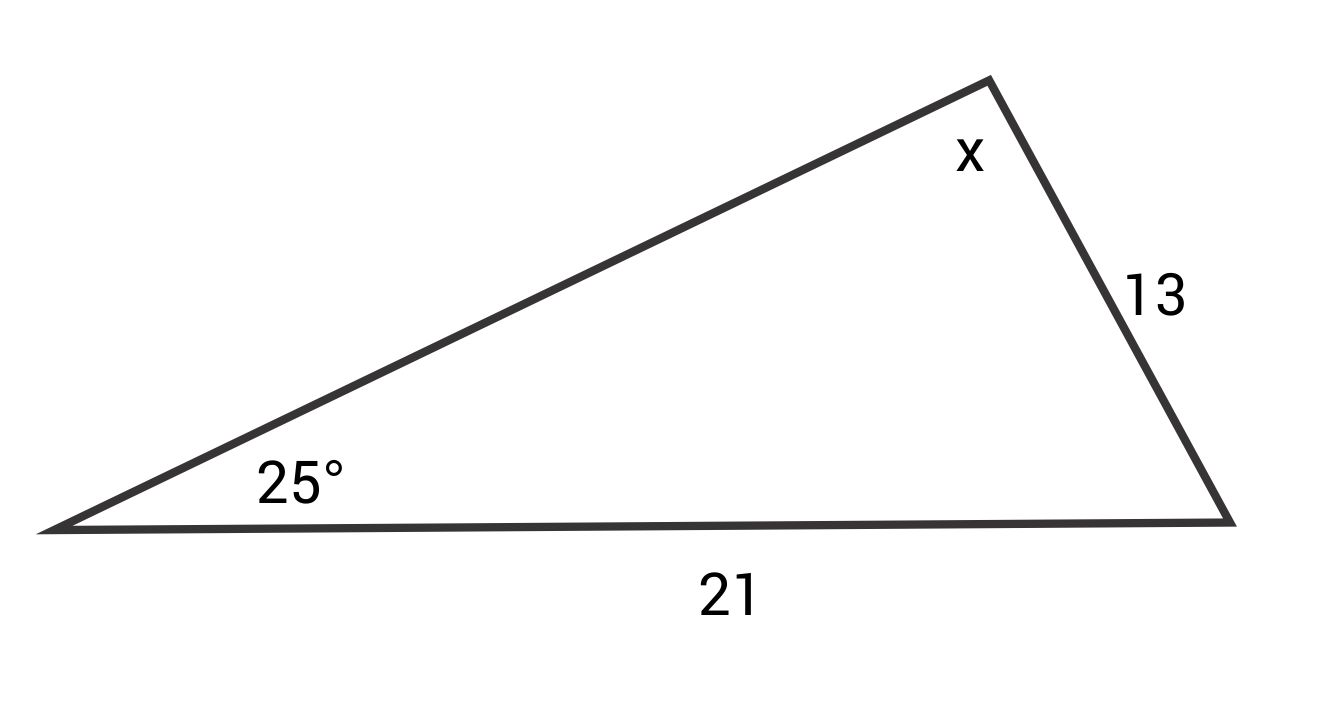
The correct answer is 43.05°. The Law of Sines states:
\(\frac{\text{sin }a}{A}=\frac{\text{sin }b}{B}=\frac{\text{sin }c}{C}\)
Filling in the information from this triangle gives:
\(\frac{\text{sin }25°}{13}=\frac{\text{sin }x}{21}\)
Manipulate to solve for x.
\(21\text{ sin }25°=13\text{ sin }x\)
\(\frac{21\text{ sin }25°}{13}=\text{sin }x\)
\(\text{sin}^{-1}(\frac{21\text{ sin }25°}{13})=x\)
\(x≈43.05°\)
Solve for x.
58.91°
39.84°
47.17°
51.02°
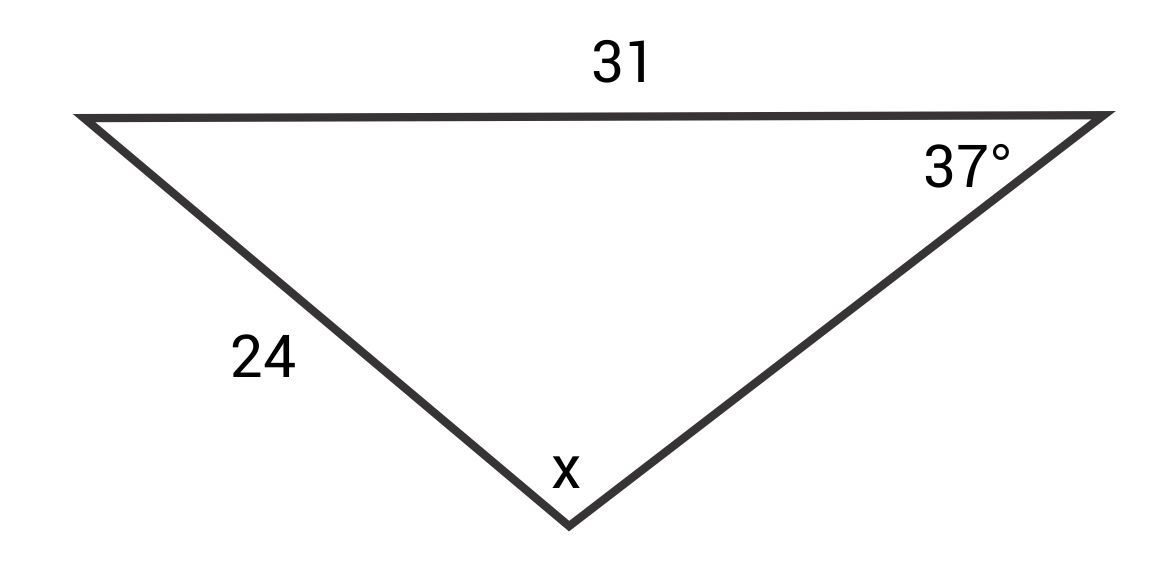
The correct answer is 51.02°. The Law of Sines states:
\(\frac{\text{sin }a}{A}=\frac{\text{sin }b}{B}=\frac{\text{sin }c}{C}\)
Filling in the information from this triangle gives:
\(\frac{\text{sin }37°}{24}=\frac{\text{sin }x}{31}\)
Manipulate to solve for x.
\(31\text{ sin }37°=24\text{ sin }x\)
\(\frac{31\text{ sin }37°}{24}=\text{sin }x\)
\(\text{sin}^{-1}(\frac{31\text{ sin }37°}{24})=x\)
\(x≈51.02°\)
Solve for x.
29.86
31.48
27.96
22.47
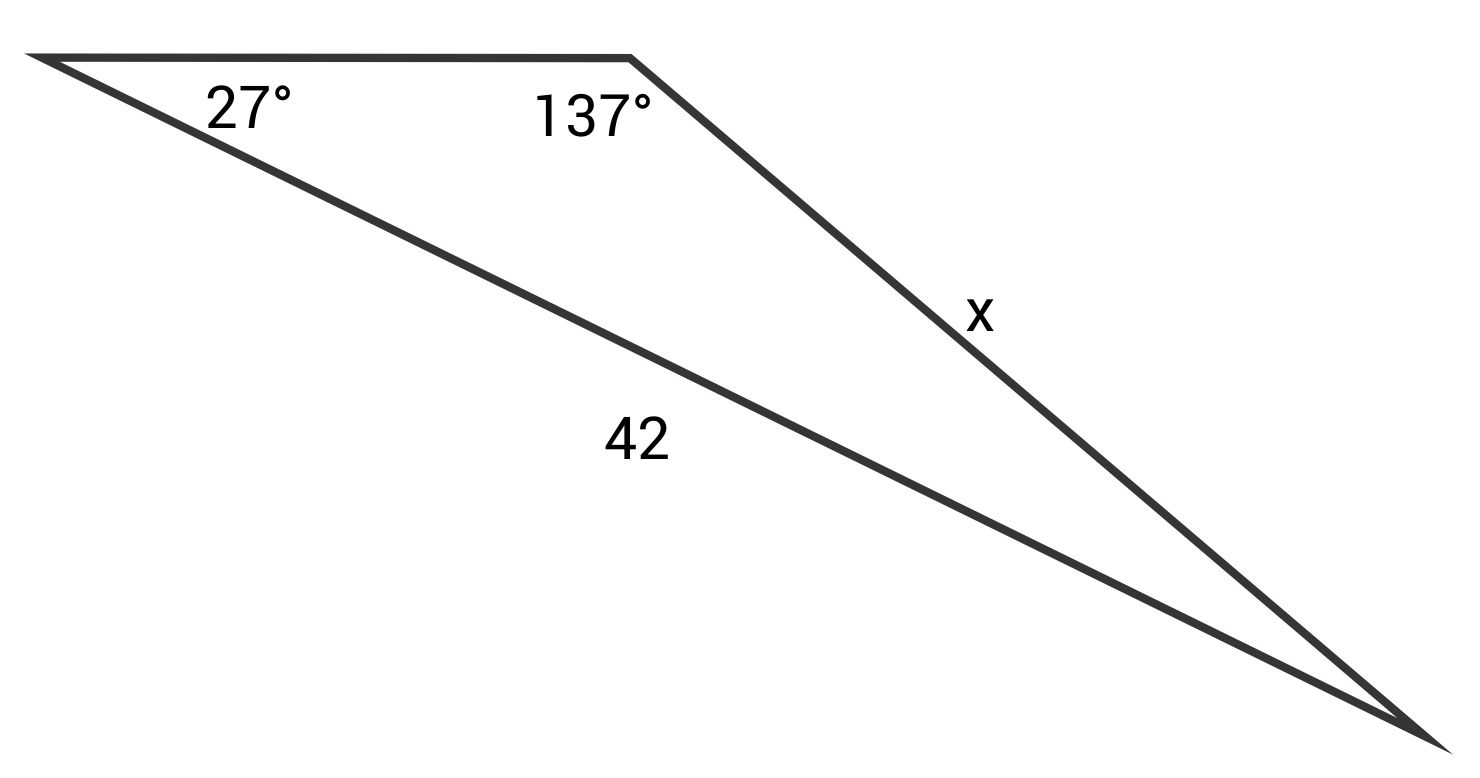
The correct answer is 27.96. The Law of Sines states:
\(\frac{\text{sin }a}{A}=\frac{\text{sin }b}{B}=\frac{\text{sin }c}{C}\)
Filling in the information from this triangle gives:
\(\frac{\text{sin }137°}{42}=\frac{\text{sin }27°}{x}\)
Manipulate to isolate x.
\(x\text{ sin }137°=42\text{ sin }27°\)
\(x=\frac{42\text{ sin }27°}{\text{sin }137°}\)
\(x≈27.96\)