
How often do you break laws? Hopefully not too often, but you may actually be breaking more laws than you think!
I’m not talking about just missing a speed limit sign; I’m talking about mathematical laws that help us take the most optimal route toward a correct answer.
In this video, we’re going to take a look specifically at the law of cosines and how it simplifies finding angles.
Pythagorean Theorem
Let’s start by taking a look at the Pythagorean theorem.
It’s that easy-to-remember formula for finding the longest side of a right triangle when we know the length of the other two sides.
Since we know that the Pythagorean theorem only works when there is a 90° angle, what happens when you’re working with a triangle that isn’t a right triangle? That’s where the law of cosines comes in—it allows us to find the third length of any triangle.
Pythagorean Theorem Formula
Here’s the formula:
As you can see from the end of the formula, we need one more piece of information than the Pythagorean theorem requires—we need the measure of an angle. To be specific, we need the measure of the angle between the two sides we know (sides \(a\) and \(b\)).
Here’s triangle ABC with the sides labeled lowercase a, b, and c:
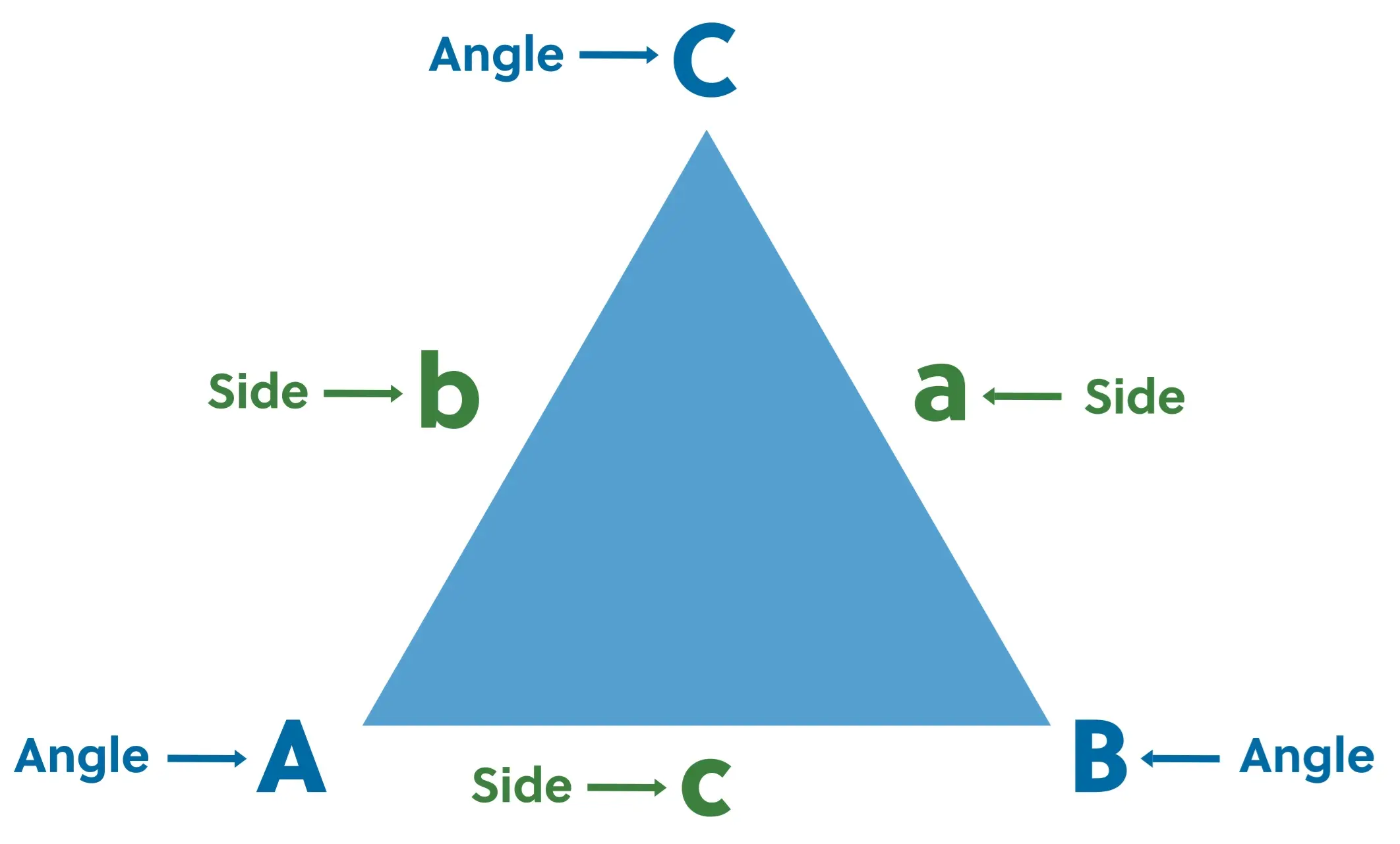
It’s important to know that, when naming a triangle, we use capital letters. And, to indicate sides, lowercase letters are used that match the opposite angle label. For example, side \(a\) is opposite angle \(A\).
So in order to use the law of cosines to find side \(c\), we would need to know side \(b\), side \(a\), and angle \(C\), which is opposite side \(c\).
Pythagorean Theorem Examples
Example 1
Let’s try it out.
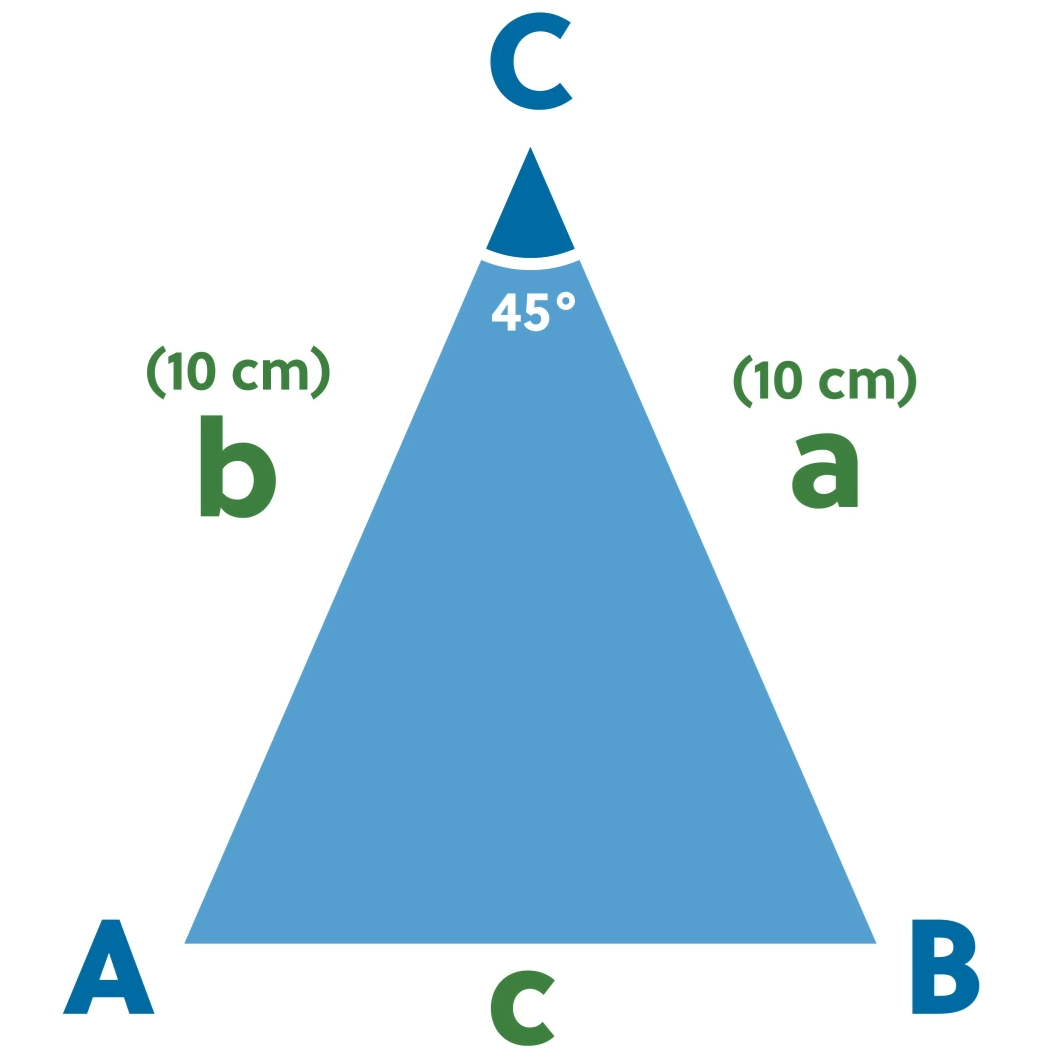
First, we need to check to see if we have everything we need to use the law of cosines. We have the measure of two sides (\(a\) and \(b\), both 10 centimeters), and the angle between those two sides is angle \(C\), which measures 45°. That’s all we need to know, so let’s plug sides \(a\) and \(b\) and angle \(C\) into the formula:
\(c^2=10^2+10^2-2(10)(10)\text{ cos}(45)\)
Be careful with the order of operations here. Evaluate the exponents first, then take the cosine of 45. Since 10 squared is equal to 100, substitute 100 for 10 squared in both places. Then, multiply 2 times 10 times 10, which is equal to 200. Then, find the cosine of 45 degrees.
\(c^2=200-144.42\)
Find the difference between 200 and 141.42.
When we get to the point where we have \(c^2\) equal to a number, we take the square root of each side to find that \(c\) is approximately 7.65 centimeters.
A common sense check of that answer tells us that it’s reasonable since sides \(a\) and \(b\) both measure 10 centimeters and their opposite angles are larger than angle C, so our answer should be under 10 (which it is).
That’s all there is to using the law of cosines for finding the missing side of a triangle. In fact, it’s a bit more versatile than the Pythagorean theorem because we can label any of the sides \(a\), \(b\) and \(c\), as long as we label the angle opposite that side \(A\), \(B\), and \(C\).
Example 2
Let’s look at another problem.
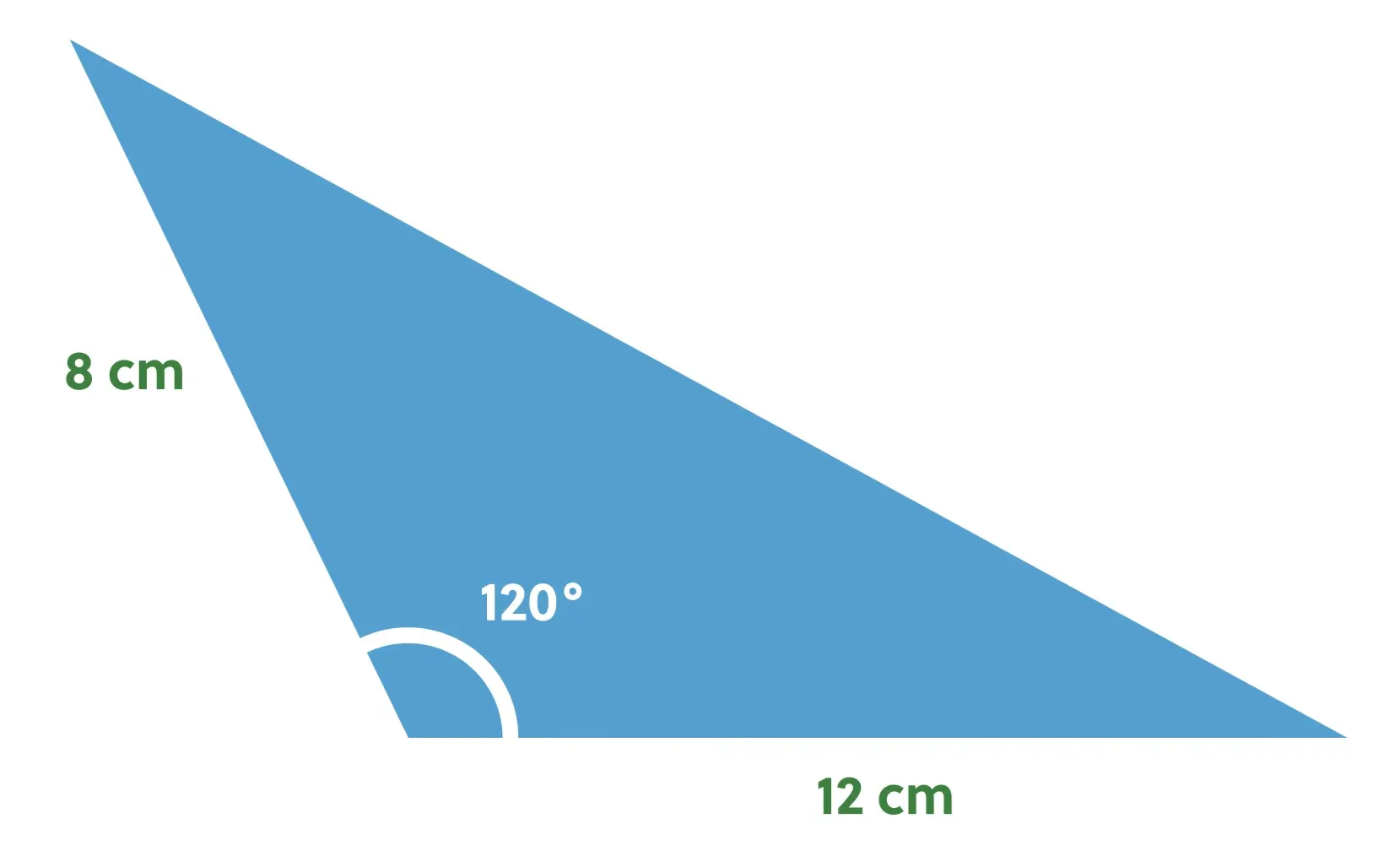
We haven’t named any of the sides or angles yet, but we can see that we have been given the measure of two of the sides and the angle between them. So we should label the angle \(C\) and the sides \(a\) and \(b\), like this:
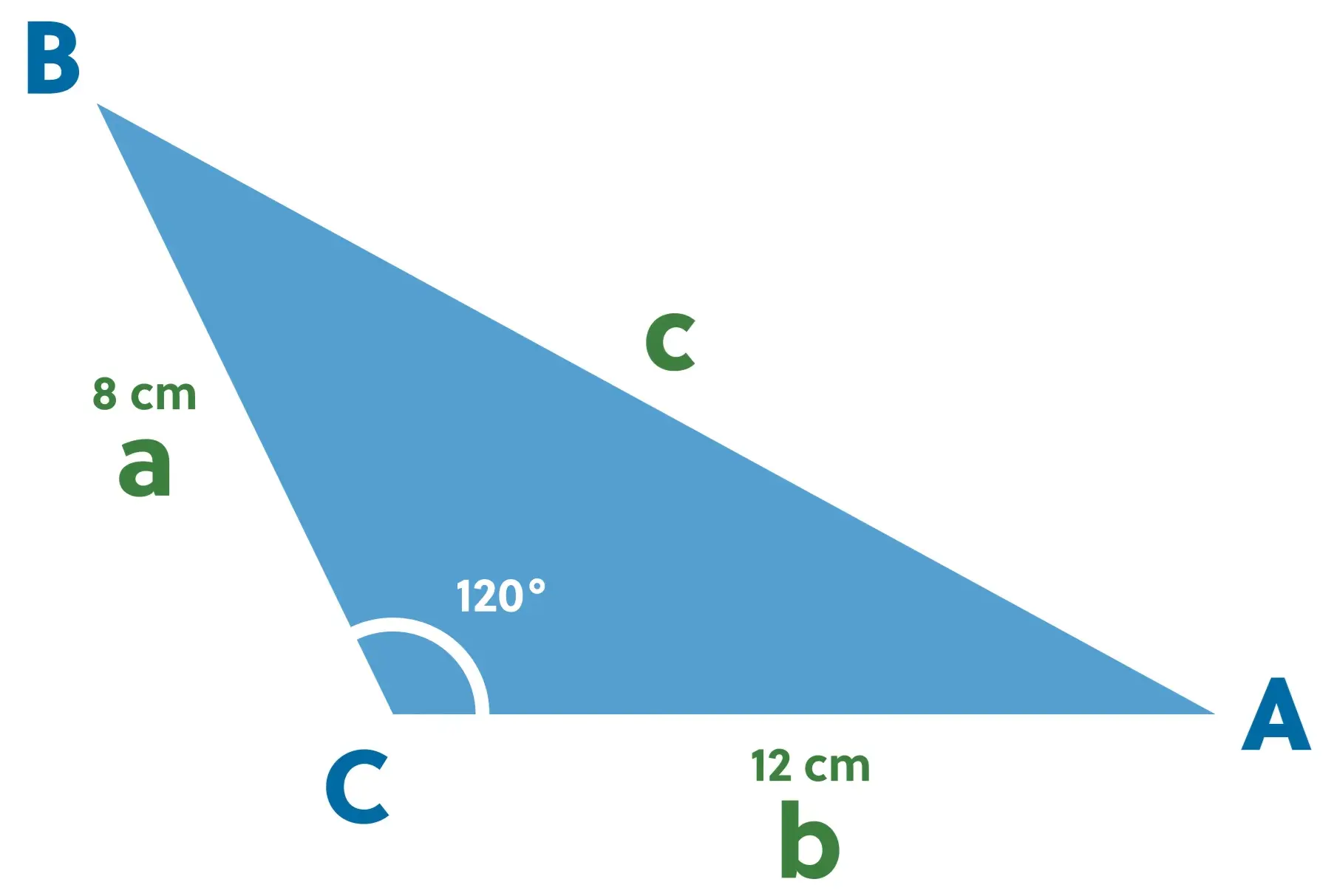
Now we can go ahead and substitute the values into the law of cosines formula that we used previously.
\(c^2=(8)^2+(12)^2-2(8)(12)\text{ cos}(120)\)
Since \(8^2=64\), substitute that value in. Since \(12^2=144\), substitute that value in as well. Then, we know that \(2\times 8 \times 12=192\). Finally, the cosine of 120° is equal to -0.5.
Add 64 and 144 together to compose a sum of 208. Then, multiply -192 times -0.5 to get a product of 96.
Then, add 208 and 96 to get a sum of 304.
Take the square root of 304.
\(c≅17.44\text{ cm}\)
Let’s try our common sense check again. Side \(c\) is opposite the largest angle, so it should be larger than the other sides (and it is). It’s also less than the sum of the other two sides, which it must be in order for this shape to be a triangle.
Okay, that’s all for this review. Don’t break the law of cosines or else the math police will come after you!
Thanks for watching, and happy studying!
Law of Cosines Practice Questions
In order to solve for the missing third side length of a triangle using the Law of Cosines, the _________________ and the _______________________ need to be provided.
The Law of Cosines is useful for determining the missing third side length of a triangle, or the angles of a triangle when you know all three side lengths. In order to determine the missing third side length of a triangle, you need to know the measure of two sides, and the angle measure between them.
Which equation correctly shows the Law of Cosines?
The Law of Cosines is useful for determining the missing third side of a triangle, or the angles of a triangle when you know all three side lengths. The formula resembles the Pythagorean Theorem, except the Law of Cosines works for any triangle, not just right triangles.
Solve for the missing side length \(c\).
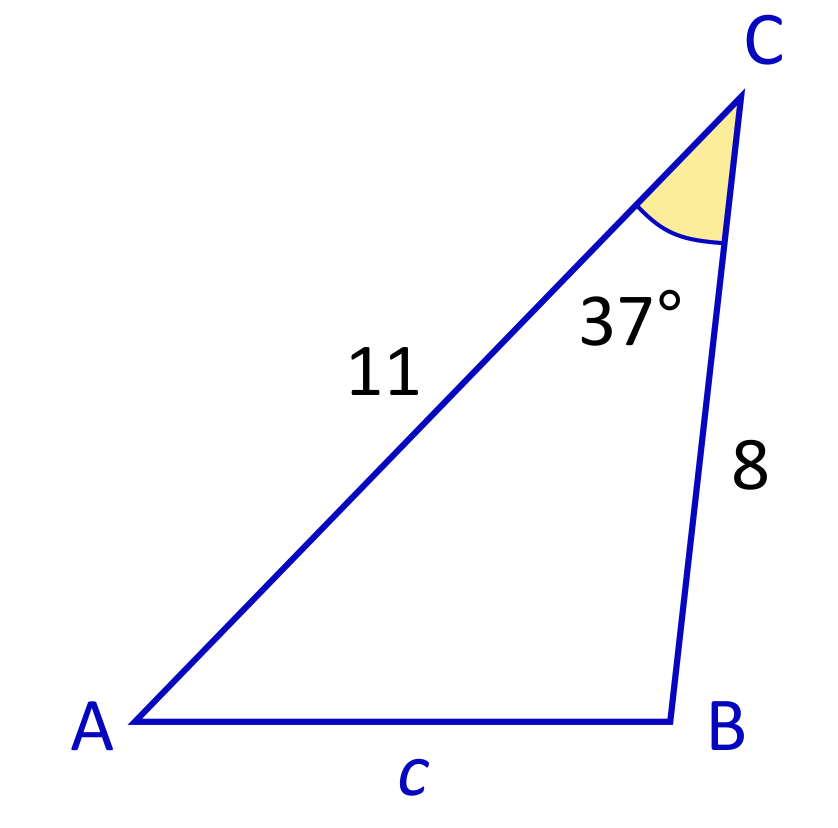
The missing side length c can be calculated using the Law of Cosines. The formula \(c^2=a^2+b^2-2ab\text{cos}(C)\) becomes \(c^2=8^2+11^2-(2\times8\times11)\text{cos}(37)\) when the provided values are plugged in. \(\text{cos}(37)\) is approximately \(0.7986\), so this can also be plugged into the formula. When the order of operations is carefully followed, \(c^2=8^2+11^2-(2\times8\times11)\text{cos}(37)\) simplifies to \(c^2\approx44.45\). Now the square root of both sides can be calculated, which means that \(c\approx6.67\).
Dan wants to measure the distance across the pond in his backyard. The pond is too shallow to use a boat to measure the distance, so Dan decides to apply his knowledge of the Law of Cosines to make the measurement. He stands back from the pond, and measures 800 feet to one end of the pond, and 900 feet to the other end. The angle between these distances is 70°. What will the distance across the pond be?
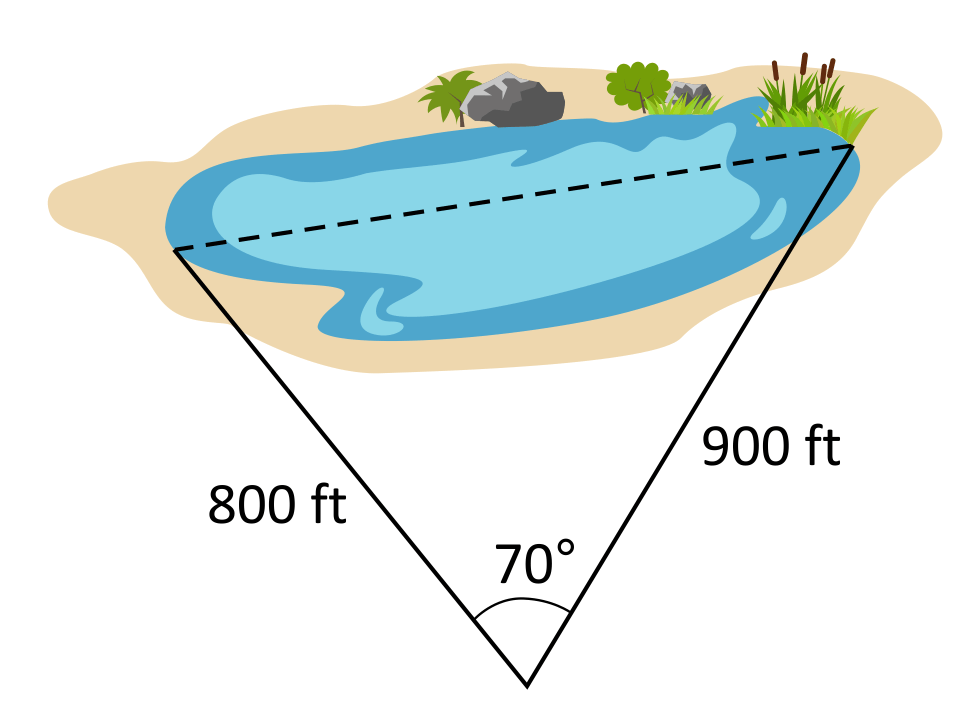
The Law of Cosines can be used to determine the distance across the pond because two side lengths are known, as well as the angle between them. The formula \(c^2=a^2+b^2-2ab\text{ cos}(C)\) becomes \(c^2=800^2+900^2-(2\times800\times900)\text{cos}(70)\) which simplifies to \(c^2\approx3{,}420.2\). When the square root of both sides of the equation is calculated, \(c\approx978.5\text{ feet}\).
Megan is designing a triangular park for her city. She needs one length of the park to be 1 mile, and another length of the park to be 2 miles. The angle between these two sides needs to be 54°. How long will the third side of the triangular park be?
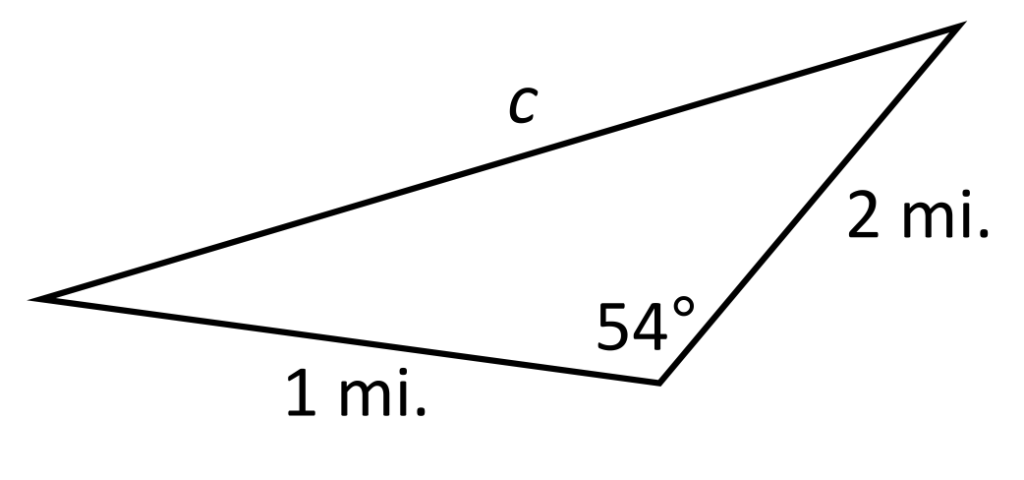
Two side lengths of the park are provided, as well as the angle in between them. This means that the third side of the triangular park can be calculated using the Law of Cosines. The formula \(c^2=a^2+b^2-2ab\text{cos}(C)\) becomes \(c^2=1^2+2^2-(2\times1\times2)\text{cos}(54)\) when the provided values are plugged in. When the order of operations are carefully applied, \(c^2=1^2+2^2-(2\times1\times2)\text{cos}(54)\) simplifies to \(c^2\approx2.65\). When the square roots of both sides are calculated, \(c\approx1.63\text{ miles}\).