There are many ways to graph a linear function. If the linear function is given in slope-intercept form, use the slope and y-intercept that can be identified from the function, \(y=mx+b\).
To graph \(y=\frac{2}{3}x-4\), which is written in slope-intercept form, we know, the \(y\)-intercept, which is where the line intersects the \(y\)-axis, is \(-4\). We start by plotting a point at \((0,-4)\). The slope of the line, which determines the steepness of the line, is \(\frac{2}{3}\).
The slope of a line is also defined as \(\frac{\text{rise}}{\text{run}}\), therefore, move up two units and to the right three units to find the next point on the line, which is \((3,-2)\). Repeat one more time from \((3,-2)\), move up three units and to the right two units to find the point \((6,0)\), which happens to be the \(x\)-intercept, or the point where the line intersects the \(x\)-axis, this is also called the zero of the linear function, which is the value of the independent variable when the value of the dependent variable is zero. Connect the dots to create the graph of the linear function.
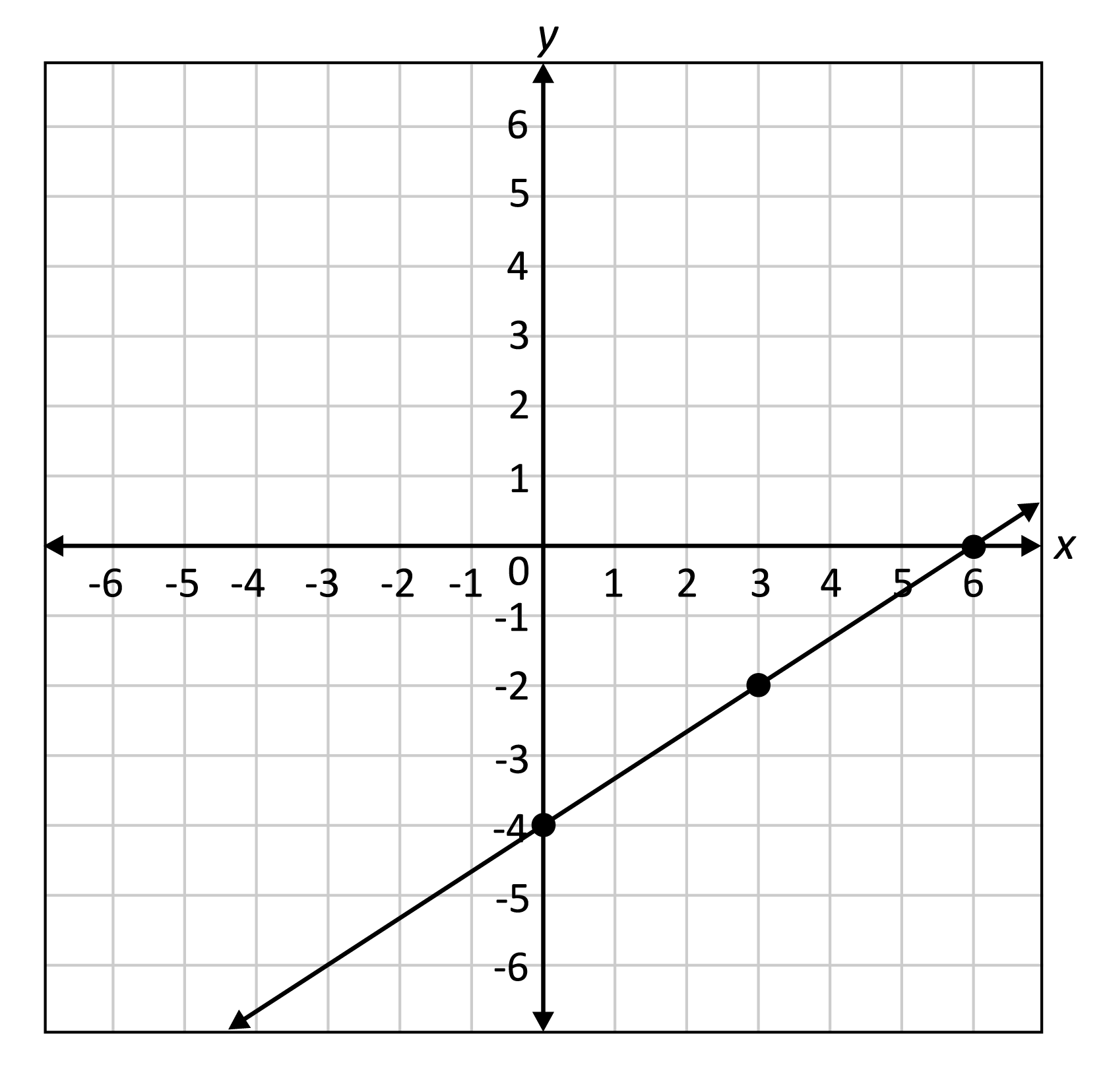
Example:
Here is the graph of a linear function.
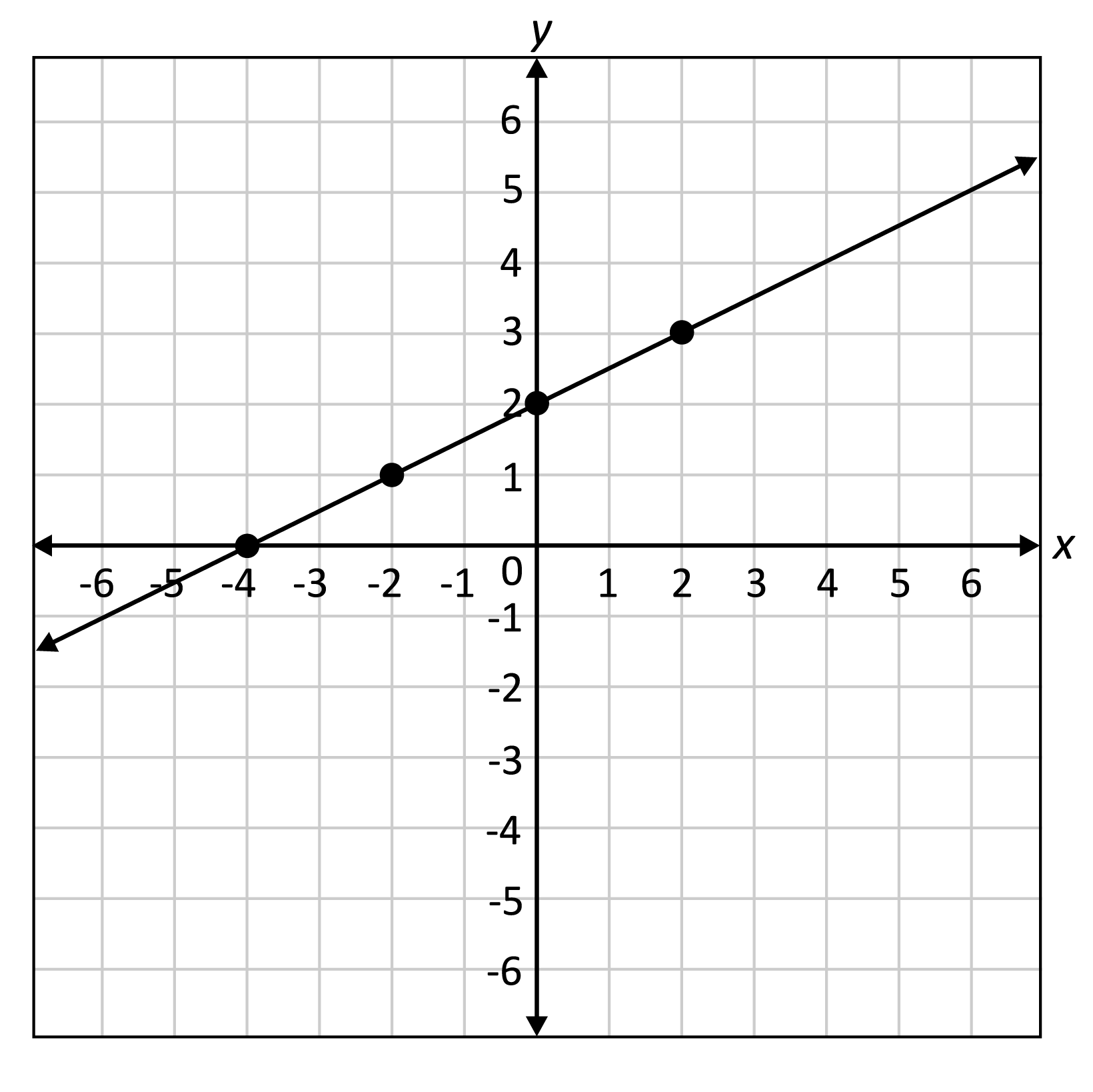
Identify the slope, \(y\)-intercept, and \(x\)-intercept of the linear function.
The \(y\)-intercept is the point where the linear function intersects the \(y\)-axis, which is (0, 2). The \(x\)-intercept is the point where the linear function intersects the \(x\)-axis, which is \((-4,0)\). The slope is found by dividing the rise by the run between two points. Use the \(x\)-intercept, \((-4,0)\), as a starting point, how many units do we rise, which is a vertical movement, and run, which is a horizontal movement, to get to the next point, which is \((-2,1)\)? In this case, we go up one unit and to the right two units to get to the next point, therefore, the slope of the line is \(\frac{1}{2}\).

Key Features of Linear Function Graphs Sample Questions
Here are a few sample questions going over key features of linear function graphs.
What is the y-intercept of the linear function \(y=-2x+8\)?
Since the linear function is written in slope-intercept form we can identify the \(y\)-intercept from the function by looking for the value of \(b\) in \(y=mx+b\), which in this case is \(8\). Therefore, the point where the linear equation intersects the \(y\)-axis is \((0,8)\).
What is the slope of the linear function \(y=-\frac{1}{3}x-4\)?
The slope-intercept form of the linear function, \(y=mx+b\), reveals the slope, \(m\), and the \(y\)-intercept, \(b\). In this linear function, the slope of the function is the coefficient of the variable \(x\), which is \(-\frac{1}{3}\).
Here is the graph of a linear function.
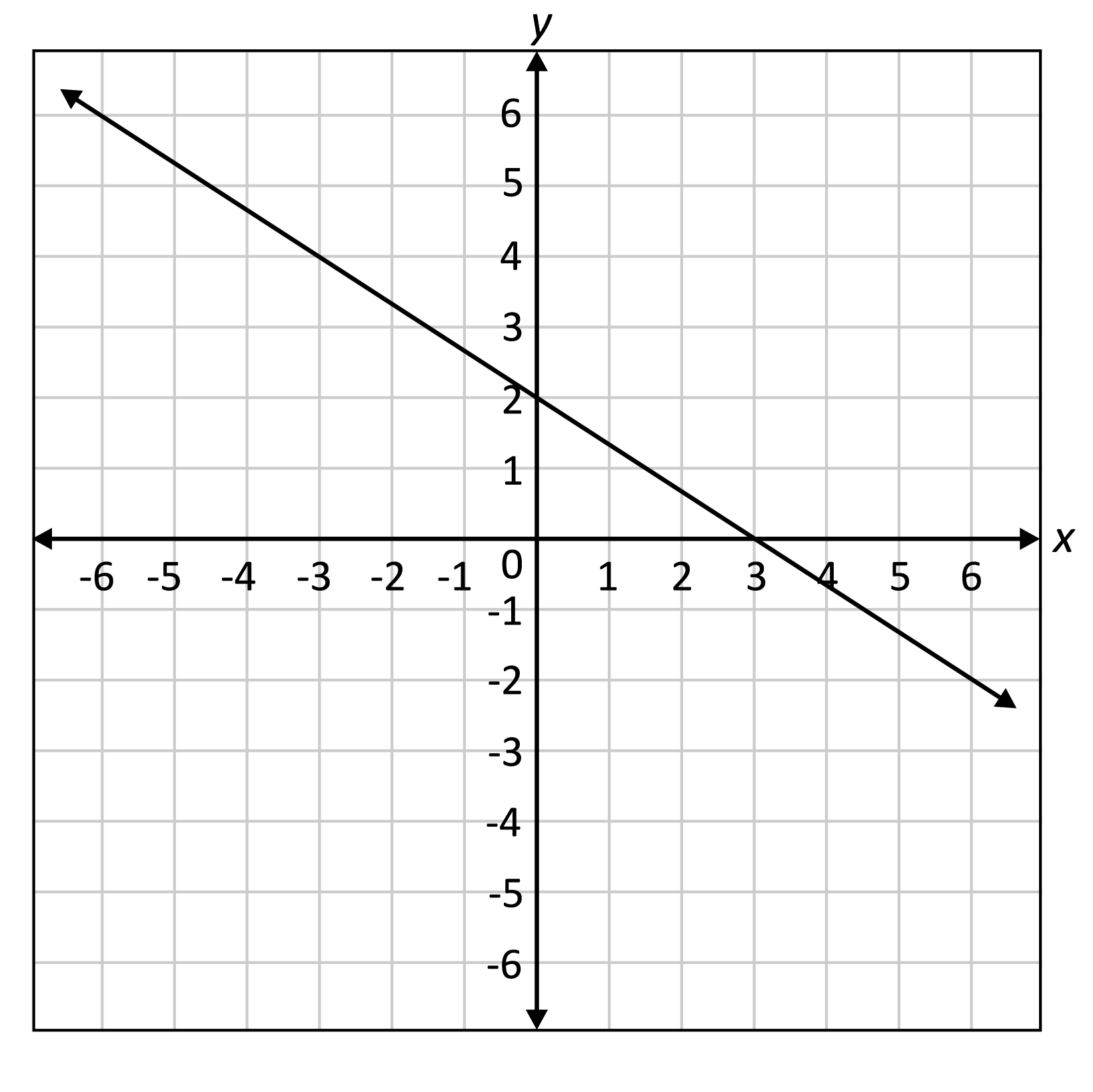
What is the x-intercept of the linear function shown on the coordinate plane?
The definition of x-intercept is the point where the graph intersects the \(x\)-axis. Looking at the graph of the linear function, we can see that the line intersects the \(x\)-axis at the point \((3,0)\).
The graph of a linear function is shown.
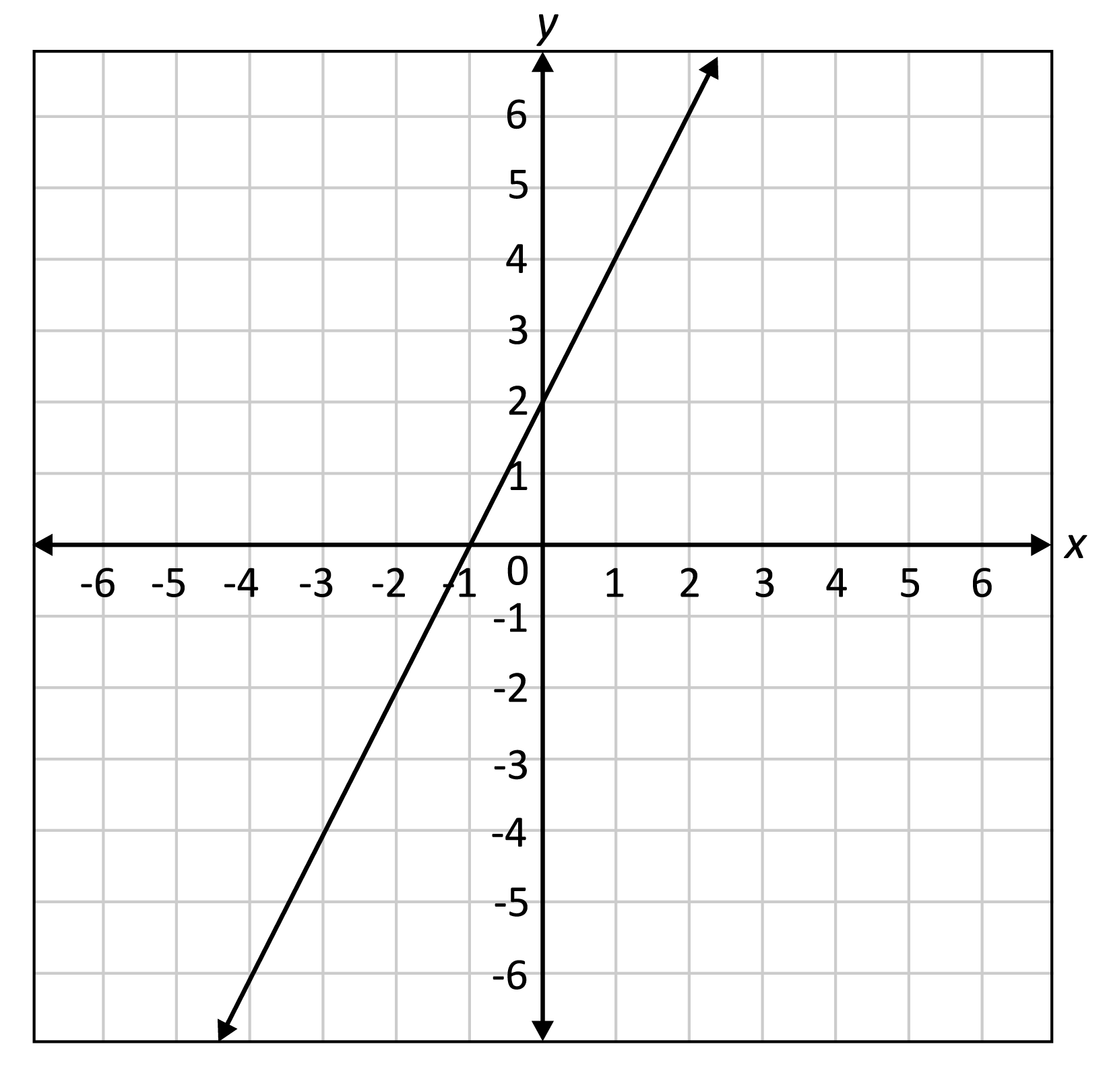
What is the zero of the linear function?
The zero of a function is the value of the independent variable (typically \(x\)) when the value of the dependent variable (typically \(y\)) is zero, which in this case is \(-1\).
What is the slope of the linear function \(-3x+4y=12\)?
The equation of the line has not been given in slope-intercept form, so we will convert it to this form to help find the slope. Using algebra skills, we solve the equation to be in the form \(y=mx+b\), which is \(y=\frac{3}{4}x+3\). Therefore, the slope of the linear function is \(\frac{3}{4}\).